2. Ошибка системы х должна быть близка по форме к гармоническому сигналу

Допустим, на вход нелинейного элемента поступает
синусоидальный сигнал ![]() . Следовательно, выходной
сигнал нелинейного элемента
. Следовательно, выходной
сигнал нелинейного элемента ![]() , является тоже
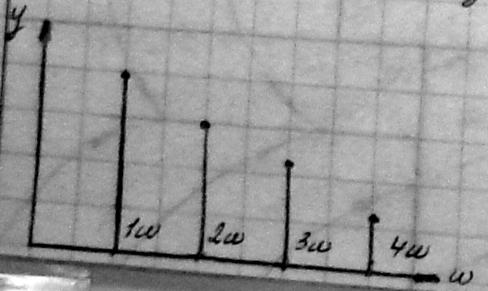
периодическим, который можно разложить в ряд Фурье . Этот ряд содержит
гармонические составляющие с частотами, кратными частоте
, является тоже
периодическим, который можно разложить в ряд Фурье . Этот ряд содержит
гармонические составляющие с частотами, кратными частоте ![]() ,
, ![]() ,
… входного сигнала
,
… входного сигнала ![]() . Полагая, что этот сигнал,
проходя через линейную часть, фильтруется до такой степени, что высшими
гармониками можно пренебречь, запишем уравнение гармонической линеаризации
нелинейного элемента:
. Полагая, что этот сигнал,
проходя через линейную часть, фильтруется до такой степени, что высшими
гармониками можно пренебречь, запишем уравнение гармонической линеаризации
нелинейного элемента:
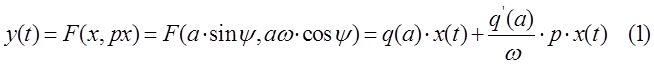
где ![]() ;
; ![]() ,
, ![]() – коэффициенты гармонической
линеаризации нелинейного элемента равны, соответственно:
– коэффициенты гармонической
линеаризации нелинейного элемента равны, соответственно:
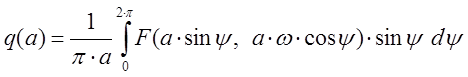 ;
;
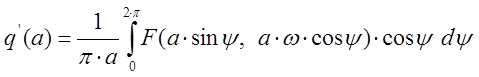 .
.
Уравнение (1) является уравнением гармонической линеаризации с точностью до высших гармоник для случая, когда нелинейный элемент имеет неоднозначную характеристику. Для случая, когда Н.Э. имеет однозначную характеристику уравнение (1) примет вид:
![]() .
.
7.2. Классификация адаптивных САУ
1) По виду информации используемой в контуре адаптации адаптивные системы делятся на:
a) Адаптивные системы управления с разомкнутым контуром
b) Адаптивные системы с замкнутым контуром адаптации
c) Комбинированные системы управления
2) По критерию качества основного контура
a) Адаптивные системы со стабилизацией качества
b) Адаптивные системы с оптимизацией качества (настройка системы на определенный критерий), обеспечение экстремального значения критерия качества
3) По средствам, используемым для адаптации
a) СНС – самонастраивающиеся системы: в этих системах адаптация за счет изменения параметров регулятора
b) СОС – самоорганизующиеся системы: адаптация происходит за счет изменения структуры системы и изменения параметров
c) СОбС – самообучающиеся системы: в этих системах используется опыт работы системы, информация о котором сохраняется в специальном блоке
4) По характеру контура адаптации
a) Системы с постоянно работающим контуром: используются когда параметры объекта управления изменяются быстро и непрерывно
b) Системы с периодически работающим контуром: параметры изменяются медленно
c) Системы с однократно включающимся контуром адаптации: используется когда объект управления имеет неизвестные начальные характеристики и его параметры постоянно или мало меняются
5) По характеру пополнения информации в контуре адаптации
a) Адаптивные системы с пассивным накоплением информации: используется для получения информации из сигналов в режиме нормального функционирования (изменение внутренних координат в системе, формирование сигнала в контуре адаптации, режим нормального функционирования)
b) Адаптивные системы с активным накоплением информации: на выход САУ подаются специальные пробные (тестовые) сигналы, по реакции на которые получают информацию об объекте управления
8.1.Гармоничсекий коэффициент передачи нелинейного элемента
В основе метода гармонической линеаризации систем – линеаризация нелинейных элементов, входящих в систему управления.
При гармонической линеаризации система управления приводится к следующему виду:
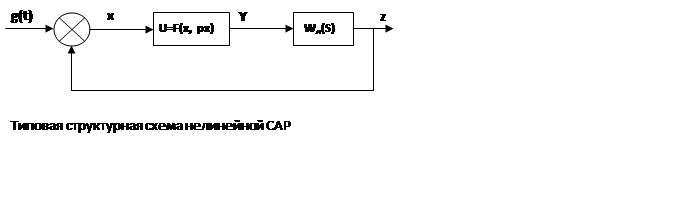
Допущения:
1. Линейная часть должна быть фильтром низких частот (то есть должна пропускать только низкие частоты)
2. Ошибка системы х должна быть близка по форме к гармоническому сигналу
Связь первых гармоник сигнала у и х характеризуется гармоническим коэффициентом линеаризации.
Допустим, на вход нелинейного элемента поступает синусоидальный сигнал ![]() . Следовательно, выходной сигнал нелинейного
элемента
. Следовательно, выходной сигнал нелинейного
элемента ![]() , является тоже периодическим,
который можно разложить в ряд Фурье . Этот ряд содержит гармонические
составляющие с частотами, кратными частоте
, является тоже периодическим,
который можно разложить в ряд Фурье . Этот ряд содержит гармонические
составляющие с частотами, кратными частоте ![]() ,
, ![]() , … входного сигнала
, … входного сигнала ![]() .
.
Так как линейная часть пропускает только основную первую гармонику сигнала y, то анализировать процессы в такой системе можно только по первой гармонике сигналов. Т. к. z и x близки к гармоническому сигналу, сигнал y можно определить после нахождения сигнала x, используя нелинейную характеристику НЭ.
Для получения коэффициентов гармонической линеаризации проводят линеаризацию нелинейных элементов.
![]() ,
, ![]() -
первые гармоники сигнала x и y,
связанные гармоническим коэффициентом передачи
-
первые гармоники сигнала x и y,
связанные гармоническим коэффициентом передачи ![]() ,
,
![]() -гармонический коэффициент передачи
(эквивалентный комплексный коэффициент передачи)
-гармонический коэффициент передачи
(эквивалентный комплексный коэффициент передачи)
Пусть
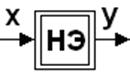
![]()
![]()
![]() (*)
(*)
Разложим функцию (*) в ряд Фурье:
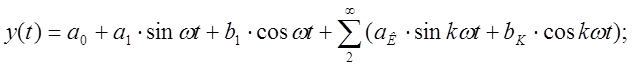 (**)
(**)
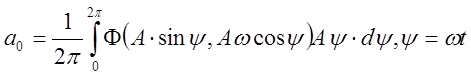
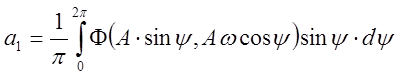 ,
, 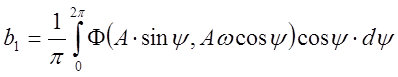
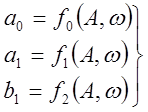 Функции от амплитуды и частоты
Функции от амплитуды и частоты
Гармоническая линеаризация сводится к отбрасыванию
в выражении (**) всех высших гармоник, находящимся под знаком суммы, пусть ![]()
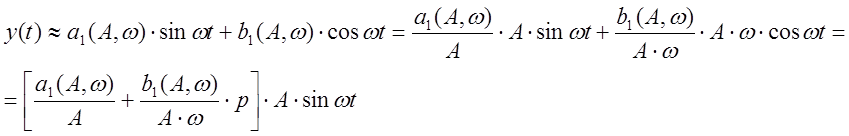 ;
;
Заменим 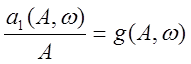 ;
; 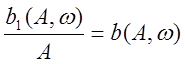 ;
где
;
где 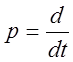
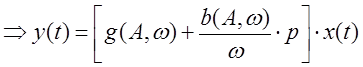
![]() ,
, ![]() - коэффициенты гармонической
линеаризации
- коэффициенты гармонической
линеаризации
Пусть ![]()
![]()
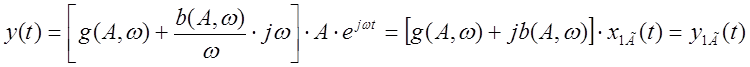
![]() - эквивалентный
комплексный коэффициент
- эквивалентный
комплексный коэффициент
8.2. Математическое описание импульсных систем. Разностные уравнения
Импульсная система реагирует на значения
воздействия, приложенного ко входу импульсного элемента только в строго
определенные моменты времени, равно отстоящие друг от друга, поэтому
непрерывное воздействие может быть заменено решетчатой функцией ![]()
Решетчатая функция определяется в дискретные моменты времени: t=0; T; 2T..nT значениями непрерывной функции, а в промежутках между этими моментами решетчатая функция равна 0.
При обозначении решетчатой функции параметр Т
постоянный и его убирают из выражения, оставляя только ![]()
![]()
Скорость изменения функции, то есть ее производная определяется
её производной первой разностью (аналог первой производной). Первая разность
или разность первого порядка обозначается ![]() и
определяется следующим соотношением:
и
определяется следующим соотношением:
![]()
Вторая разность – аналог второй производной: ![]()
Разность к-го порядка:
![]()
Может быть выражена через решетчатую функцию.
По аналогии с дифференциальными уравнениями для непрерывных систем для дискретных систем можно записать разностные уравнения.
Разностные уравнения - соотношение между решетчатой
функцией ![]() и её разностями различных порядков.
и её разностями различных порядков.
Если это соотношение линейно, то и разностное уравнение называется линейным.
Существуют две формы записи линейных разностных уравнений.
1.
![]()
2.
![]()
Дискретные САУ описываются разностными уравнениями, которые можно решить с помощью z- преобразования, которое является основным математическим аппаратом теории дискретных систем
Обычное z- преобразование решетчатой функции ![]() называется функция
называется функция ![]() , определяющаяся соотношением
, определяющаяся соотношением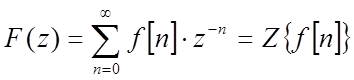 , где
, где ![]() -
параметр z- преобразования
-
параметр z- преобразования
Модифицированное z- преобразование имеет месть для
смещенной решетчатой функции![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.