Рассмотрим одинарный мост переменного тока. В качестве индикатора прим. либо аналоговый высокоомный вольтметр либо осциллограф с лин. разверткой. При этом точки a и b сх. вкл. на верт. откл. пл. (вх. Y). При вкл. ГЛИН на экр. набл. sin сигн. нек-рой амплитуды. Uab = U0sin wt. Обычно в два плеча мост. сх. вкл. переменные активные сопр., с пом. к-рых достигается равновесие моста, которое выражается в выравнивании потенциалов a и b. При этом амплитуда U0 уменьшается и при полном уст. равновесия на экр. видна только гор. полоса, созданная сигн. лин. развертки. В отл. от моста пост. тока в этой сх. необх. 2 переменных резистора. Выражение для мгновенного Uab можно получить проведя расчет эл. сх. любым известным методом.
По законам Кирхгофа сост. ур-ие для опр. неизв. токов в ветвях. Iab = 0 – усл. равновесия. Соотн. сопр. плеч внешне получается таким же, как и для моста пост. тока.
Z1Z3 = Z2Z4 (1)
Комплексные вел. предст. 2 способами – алг. и показ. форме. Z = R + jX1 = Z1e jj1.
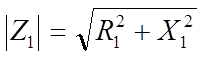
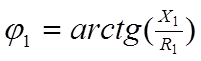
Подст. в рав. 1 компл. сопр. в показ. форме., т.е. Z1e jj1 Z3e jj3 = Z2e jj2 Z4e jj4.
Z1Z3e j(j1+j3) = Z2Z4e j(j2+j4) (2)
Z1Z3 = Z2Z4 – ампл. усл. равновесия.
j1+j3 = j2+j4 – фазовое усл. равновесия.
1)Пусть Z1 = R1, Z2 = R2.
Т.к. сопр. чисто активное, j3 = j4. Из последнего равенства следует, что реактивное вкл. в плечи 3 и 4 должны быть одинаковой природы: емкостной или индукционной.
2)Пусть Z1 = R1, Z3 = R3.
По усл. равновесия j2 = -j4. В случае такого моста нагрузки должны быть разной природы: XL и XC.
Вопрос№36 Мост Вина для измерения пар-р катушки.
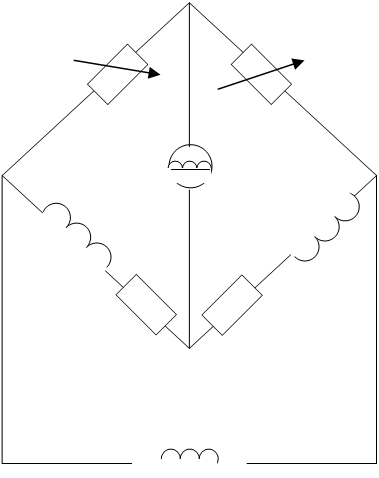Рассм. эл.схему L3 = LX – ?
R3 = RX – ? Запишем условие равновесия моста в
общем виде и подставим значение комплексных сопротивлений.
Z1Z3 = Z2Z4. R1(R3 + jwL3) = R2(R4 + jwL4).
R1R3 + jwR1L3 = R2R4 + jwR2L4.
Приравниваем действительные и мнимые части:
R1R3 = R3R4 => RX = R2R4/R1
R1L3 = R2L4 => LX = R2L4/R1
Вопрос №37. Мост Сотти (для определения характеристик
конденсаторов с малыми активными потерями).
Составим мост Сотти. С3 = СX – ? R3 = RX – ?
Запишем условие равновесия моста в общем виде и подставим значение комплексных сопротивлений.
Z1Z3 = Z2Z4. R1(R3 + 1/ jwС3) = R2(R4 + 1/ jwС4).
R1R3 + R1/ jwC3 = R2R4 + R2/ jwC4.
Приравниваем действительные и мнимые части:
R1R3 = R3R4 => RX = R2R4/R1
R1/C3 = R2/C4 => CX = R1C4/R2
Вопрос№38 Методы измерения синусоидальных сигналов.
Электрические сигналы (ток, напряжение) изм. по гармоническому закону:
u(t) = U0 sin(wt + j0)
Частота u -физич [Гц] [Гц] = с-1, связана с циклич.(круговой) частотой w по ф-ле w = 2пu,
[w]=рад/с.
Для изм. частоты исп. следующие методы:
1. Метод непоср. изм. частоты с помощью осциллографа.
а. с линейной разверткой
б. с синусоидальной разверткой
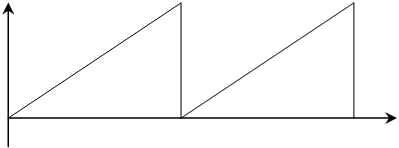
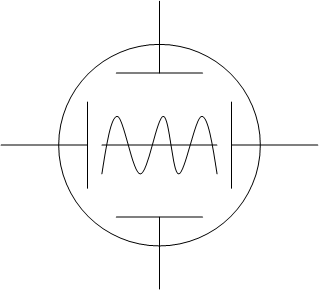В случае а на гор.
откл. пластины X от ГЛИН пост. напряжение, изм. во времени по лин. пилообразному закону.
Под возд. лин. нараст. напр. электронный луч перем. в гор. напр. с пост. скоростью. Исследуемое син. напр. неизвестной частоты wX подается на верт. откл. пластины (Y). При одновременном воздействии на эл. луч исследуемого напр. и напр. развертки, на экр. осциллографа набл. реальная зависимость вх. напр. от времени. На осциллографе имеются ручки упр., связанные с калибраторами амплитуды и длительности (В/дел., с/дел.).
Из обозн. следует, что при том или ином положении рукоятки задается значение напр. или времени по координатной сетке экр. Гор. отр. соответствует некоторому временному процессу, измеряемому в миллисекундах или микросекундах. Верт. отр. задает значение одного из отр. синусоиды. По координатной сетке можно опр. период син. напр., а значит и частоту.
В случае б на гор. откл. пластины подается не пилообразное, а синусоидальное образцовое высокостабилизированное с частотой w0 напр. (50 кГц)
Одновременно на Y-пластины подается исследуемый син. сигнал частотой wx = 2пfx. При выполнении условия кратности частот fx/f0 = n, f0/fx = m, где m и n – целые значения. Электронный луч под одновременным воздействием 2 син. напр. вычерчивает разнообразные кривые в зависимости от m и n, наз. фиг. Лиссажу. По характерному виду фигуры можно опр. значение кратности частот n и m, по к-рым опр. fx.
Простейшая фиг. Лиссажу – эллипс, при m = n = 1. В зависимости от фазового сдвига между напряжениями UX(t) и UY(t) эллипс вырождается в окружность, при фазовом сдвиге Dj = п/2 + 2пk. В прямую с полож. угл. коэф. при фазовом сдвиге 2пk. С отр. угл. коэф. при фазовом сдвиге п + 2пk. Данный метод огр., т.к. требует вып. усл. кратности частот, что не всегда возможно.
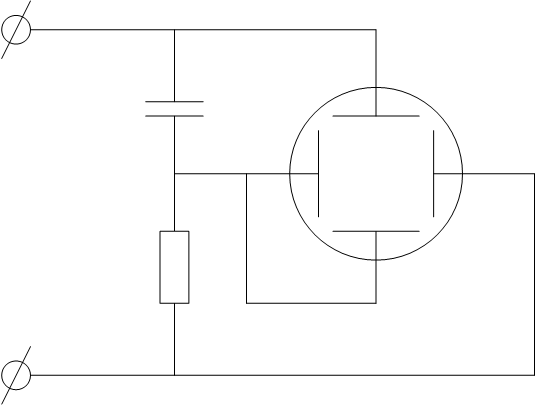2. Метод светящихся
меток на круговой развертке. Осн. на исп. обр. частоты, равной 50 кГц и спец.
устр., встроенного в приемник-компаратор, связывающего модулятор ЭЛТ с выходом Z приемника. Круговая развертка возн.
благодаря делению опорного сигнала с частотой на RC цепях. При этом ток частоты, f0 протекающий через емкость C и сопр. R создает на них падение син. напр. одинаковой частоты f0, со сдвигом по фазе –п/2.
Эти напряжения подаются на верт. и гор. откл. пластины и создают круговую развертку. Если на вход Z приемника-компаратора подается син. напр. fx, то при выполнении условия кратности fx/f0 = n, где n – целое, на круговой развертке появятся светящиеся точки (метки), число которых зависит от показателя кратности. Метод достаточно точен и используется при построении градуировочных кривых генераторов переменной частоты при их поверке.
3.
Резонансный метод. Исп. в т.н. резонансных частотомерах, которые работают, исп.
явление эл. резонанса в колебательном контуре. При выполнении условия резонанса
.
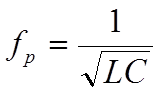L и C могут перестраиваться в узких диапазонах, поэтому резонансные частотомеры не получили широкого применения и исп. при реш. узкого круга задач.
Вопрос№39 Электронно-счетный цифровой частотомер
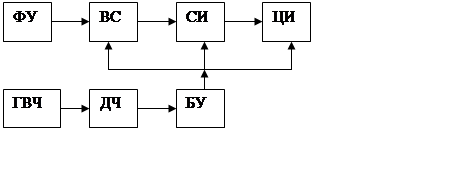Широко исп. ЭСЦЧ,
поскольку позволяет находить неизвестную частоту в диапазоне от десятков Гц до
сотен МГц.
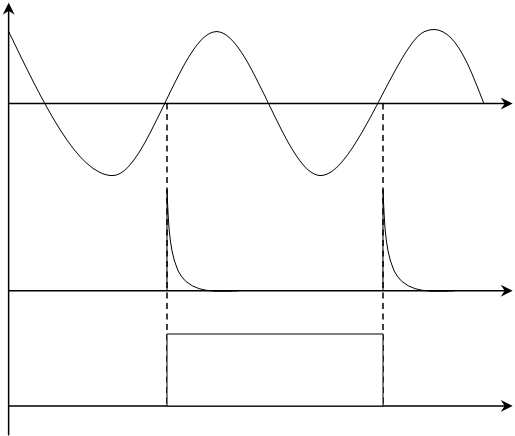ФУ – блок
формирующего устройства, преобр. син. напр. в посл. коротких импульсов полож.
полярности, с частотой следования fx, равной частоте син. сигн. Устройство вырабатывает полож.
импульс в момент перехода в 0 с «-» на «+».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.