Личностная погрешность (человеческий фактор) (связан промах или сильное (глубокое) отклонение значения измеряемой величины, по сравнению с другими значениями измеряемой величины Х в процессе проведения измерения в одних и тех же внешних условиях).
По условию возникновения систематическую подразделяют на основную и дополнительную.
Дополнительная к основной возникает когда изменяется внешние условия проведения измерения (температура, давление, влажность среды)
В отличии от случайной погрешности не существует единой универсальной методики выявления и исключения систематической погрешности.
В простейшем случае проведения измерения с помощью одного прибора систематическую инструментальную погрешность можно определить по классу точности измерительного прибора:
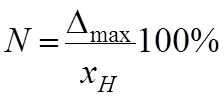
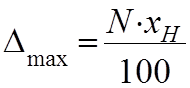
из формулы следует, что чем меньше номинальное значение измеряемой величины тем больший вклад вносит инструментальная погрешность.
Вопрос №6. Случайные погрешности измерения. Их метрологические характеристики.
Случайные – проявляются в небольшом изменении значения измеряемой величины в ту или иную сторону и возникают в результате одновременного воздействия множественных факторов.
Случайные погрешности наряду или вместе с систематической наблюдаются в процессе проведения серии прямых равноточных измерений физической величины Х, когда результатом измерения является ряд близких значений Хi измеряемой величины Х.
Основной характеристикой случайной величины измеренного значения Х, усредненное по серии значение измеренной величины, погрешность измерения и др., является функция плотности вероятности этой величины или же закон ее распределения.
f(x) – некоторая математическая формула где х – сама случайная величина.
Гистограмма получающиеся следующим образом: в процессе измерения выявляется некоторое максимальное и минимальное значение некоторой величины. Весь интервал разбивается на п – частей и выявляется частота попадания значений измеряемой величин в тот или иной интервал.
В результате строится график:
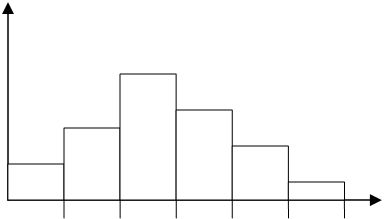
7. Гистограмма распределения случайной величины. Ф-я плотности вероятности
её распределения.
Пусть производится многократное измер–е физ. вел. х в одних и тех же внешних условиях. При этом истинное знач-е вел-ны х (ХИСТ) не известно, и в процессе измерений нах-ся оценка ХИСТ – ХДЕЙСТВ, которая при увеличении числа измерений приближается к её ист-му значению. В процессе измер-й появляются знач-я Хmin ≤ Х ≤ Хmax При этом произв-ся некоторое количество измерений (напр-р, п =50)
Нах-ся интервал измер-я Хmax- Хmin = ∆Х , который разбивается на К – равных промежутков (напр-р К = 5)
Опред-ся число знач-й измер-ой вел-ны, попадающих в каждый интервал, и строится таблица:
|
nk |
5 |
12 |
18 |
11 |
4 |
….. |
|
nk/n |
0,1 |
…. |
… |
.. |
.. |
.. |
 |
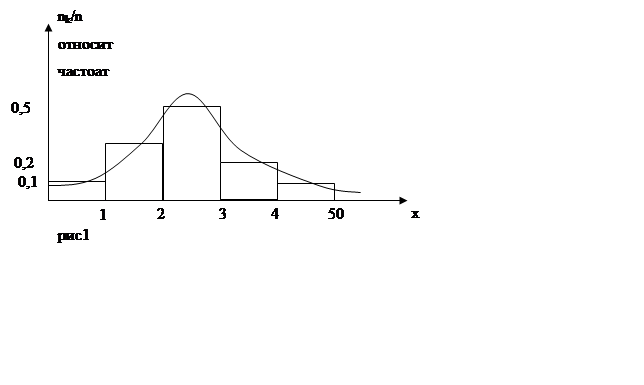Из рис1 видно, что частота измер-х значений Х достигает максимума в районе середины, что указывает на то ,что где-то в приделах этого прямоугольника находится истинное значение измеряемой величины.
Появление измеряемых значений Х , как в сторону уменьшения, от центра распределения(влево), так и в строну увеличения значений Х (право), снижается
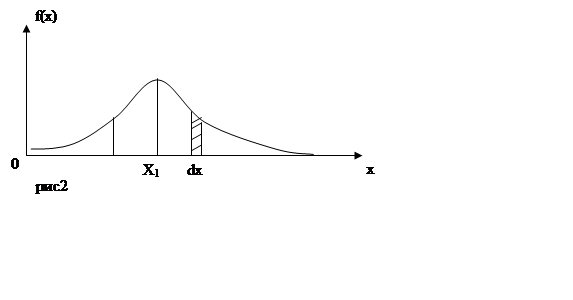Частота появления тех или иных измеренных знач-й Х определяет
вероятность получения тех или иных измер-х значений.
При увеличении числа интервалов nK ступенчатая ф-я рис1 может быть заменена некоторой плавной кривой f(x), кот-я наз-ся ф-цией плотности вер-ти появление тех или иных измер-х знач-й величины Х, а dP = f(x)dx – вероятность показания тех или иных измеренных значений вел-ны х в тот или иной интервал dx
При этом поведение ф-и f(x) практически повторяет ход гистограммы.
Явный вид функции f(x), т.е. вер-ти появления того или иного значения х в процессе измерения называется законом распределения случайной вел-ны х.
Наиболее вер-е значение –Х1 - max f(x).
Знач-е Х1 – мода распределения.
Наблюдаются различные виды ф-и f(x) или разл-е виды з-ков распред-я Х
Законы
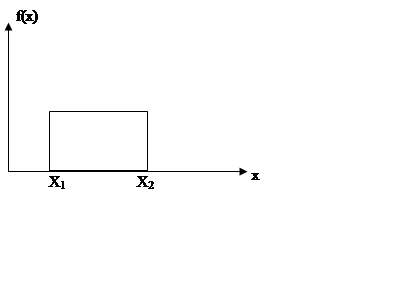равномерное распр-е
вероятности появления случ-х вел-п в некотором ограниченном интервале х
(отсутсвуетмода)
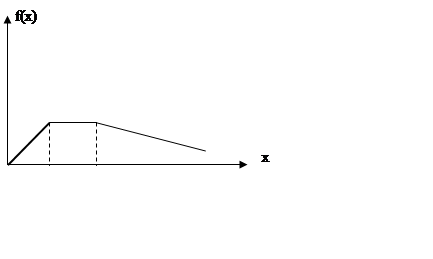Треугольный закон
распределения случайной величины
Трансцеидальный закон распределения
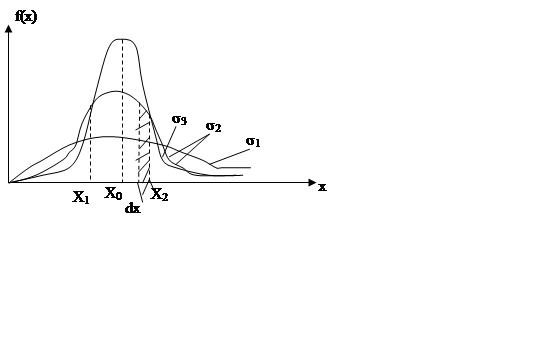
Нормальный закон распределения
Наиболее часто проявляется при поведении серии прямых равноточных измерений одной и тоже величине х при большом количестве измерений(п ≥ 15) п ≥15 – серия большой выборки п < 15малой выборки
Особенности закона норм распределения
1) имеется явно выраженный центр (мода) закона распределения
2) ход кривой ф-и f(x) симметричен относительно центра распределения, т.е вер-ть появления измеренных значений величины х, симметричных относительно центра, становится одинаковой при большом числе измерений
3)Рассеяние измеренных значений относительно центра уменьшается с уменьшением пар-ра σ, где
σ – среднеквадратичное отклонение (СКО) f(x), опред-ся по результатам измер-й
Вер-ть для данного значения σ появления измеренного знач-я Х в интервале dx численно равна заданной на площади квадратной трапеции, делённой на площадь фигуры ограниченной кр-й распределения и осью Х(вер-ть≤1) реал-е значение вер-ти события(вер-ть достоверн события) = 1
Ф-ия f(x) нормируется на 1-цу так называемым углом нормировки
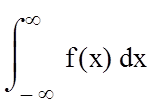
(1)
Равенство (1) показывает, что любое измеренное значение величины х в интервале (-∞ ;+∞) явл-ся событием достоверным, вер-ть которого=1
Интеграл имеет геометрический смысл площади отсюда следует, что площади ограниченные кривыми норм. закон распред. для разных σ, одинаковы и равны 1
Вопрос №8. Характеристики закона распределения случайной величины (мода, Д, σ).
Явный вид функции, графиком которой является кривая нормального распределения, получил немецкий математик Гаусс, поэтому закон нормального распределения Х называется законом Гаусса, который имеет вид:
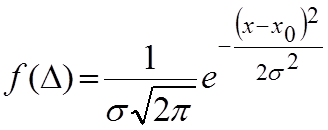(1)
Х0 – центр распределения
Употребляется также математическое ожидание случайной величины.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.