Физическая величина свойства и единства измерения физических величин. Измерения. Шкалы измерений. Классификация измерений. Средства измерений. Погрешность измерения и их классификация, страница 4

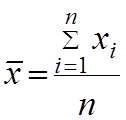
2. Находится абсолютная погрешности измерений

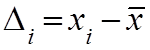
при этом Δ входит, как со знаком «+» максимум и с «-»

3. Проверяется нормальность закона распределения Δ. Известно, что модой нормального распределения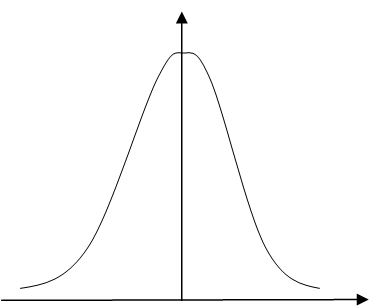 f(Δ) является 0.

Поэтому сумма всех Δ-й.

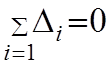
4. Если f(Δ) не подчиняется закону Гаусса, то полученное Δi проверяется промахи.

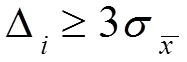
5.

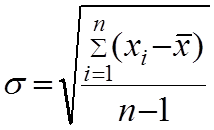
6.

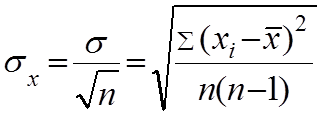
7. Если некоторая Δi является промахами, то они исключаются из серии измерений (возвращаемся к пункту 3). В результате исключения промахов: 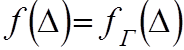. После процедуры 5 и 6 повторяются.

8. для вычисления доверительного интервала Δm, необходимо задаться значением доверительной вероятности. Типичным значением р является значение вероятности равной 0,95. задавшись значением р мы утверждаем, что с 95% вероятностью все значения погрешности Δi войдут в доверительные границы – искомому Δi.

С помощью таблиц интеграла Лапласа находятся значение верхнего предела интеграла Лапласа Zn, при этом, как было показано границы доверительного интервала .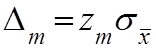

9. 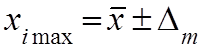 (математическое ожидание).

Δm – максимальное значение абсолютной погрешности, имеющей случайных характер.

Однако, кроме случайной погрешности, может присутствовать и не исключаемая систематическая погрешность, оцениваемая своим максимальным значением или границей (НСП).

В теории погрешности 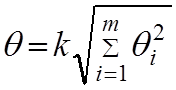 (θ - тетта), где

 - не исключенная НСП соответствующего номера.

В самом простейшем случае, если исключить личностную погрешность, выбрана самая удачная методика измерений и саамы измерения проводятся одним единственным прибором, то в этом случае граница НСП определяется классом точности измеряемым прибора по формуле.

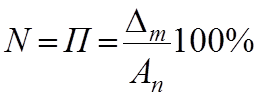
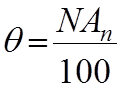 - класс точности.

При этом коэффициент К зависит от доверительной вероятности. При р=0,5, К=1,1.

Найдя θ, поступают следующим образом:

А) Если 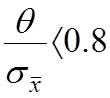, то не исключена систематическая погрешность (НСП) пренебрегают, т.е погрешность считают частично случайной с максимальным значением Δm.

Б) Если 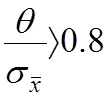, то пренебрегают случайной ошибкой и в этом случае границы общей погрешности принимают θ.

                            

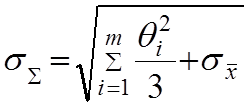
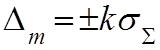
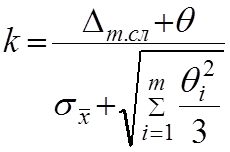
Вопрос №13. Статическая обработка серии малой выборки.

Серия малой выборки n<15.

С уменьшением числа измерений в серии закон распределения самой случайной величины f(x), а также закон распределения Δ все более отклоняются от нормального.

Английский математик Госсет нашел вид этого распределения основным свойством которого является то, что при п→∞,

Используя полученную формулу, Госсет построил таблицы по типу таблиц интеграла Лапласа, по которым находится верхний предел интеграла вероятности с подынтегральной функцией . Значение верхнего предела обозначается буквой t, значение которой находится по таблице при заданной значение р и п.

t – называется коэффициентом Стьюдента, которой используется для нахождения доверительной границы случайного характера.

.

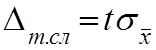Весь остальной порядок нахождения математического ожидания остается таким же, как и в нормальном случае.

Вопрос №14. Погрешность косвенного измерения.

Измерение называется косвенным, если результатом такого измерения насчитываются по известной математической формуле.

Как правило, абсолютная погрешность измеряемой физической величины имеет ту же размерность, что и сама величина и является величиной малой, если она не является промахом.

Т.е по смыслу абсолютная погрешность измерения приближается к понятию дифференциала величины Х, т.е. к бесконечно малому отклонению от истинного значения.

.

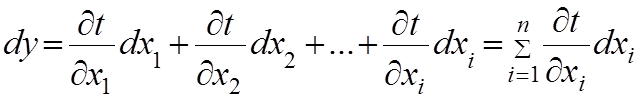Однако эта формула имеет недостаток, что частные производные могут иметь различные знаки.

В теории ошибок доказывается, что складывается не из самих погрешностей, а из их квадратов, т.е. дисперсии случайной величины.

Поэтому абсолютная погрешность косвенного измерения определяется по формуле:

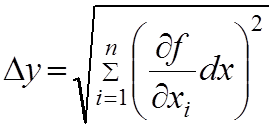
Вопрос №15. Задача совместного измерения. Функция аппроксимации.

В результате проведения совместимого измерений определяется прямым измерением искомая величина Y. Так и определяется другая измеряемая .(1)

 -неявная функция одной величины Х (2)

yi	xi
y1	x1
y2	x2
…	…
yn	xn

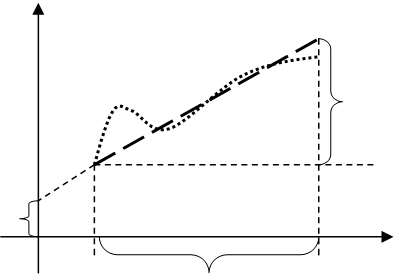Основной задачей совместного измерения является подбор такой математической зависимости (2) или (1), чтобы она наилучшем образом описывала экспериментальное поле точек.

А именно в качестве критерия выбирается минимальное отклонение экспериментальных точек от теоретической кривой. Для этого применяется различные известные математические зависимости – функции аппроксимации.

1). Линейная зависимость. (y(x))

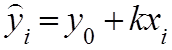 (3)

в каждой точке устанавливается связь между х и у

 - теоретическая функция                                      y – экспериментальное значение

В пределах проведенного эксперимента мы можем иметь следующее данные.

Экспериментальный интервал значений Х

Интервал значений Y.

Коэффициент К входящий в уравнение (3) называется угловым коэффициентом который равен тангенсу угла наклона прямой к оси абсцис:

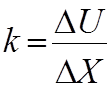
2). Показательная функция.

 (4).

Возьмем натуральный логарифм от уравнения (4).

 (5)

Если поле точек может быть описано функцией (4), то график поля точек в логарифмических координатах будет близок к зависимости (5)

In yi	xi

3). Степенная функция.

 (6)

Для определения параметров аппроксимации а и в, возьмем логарифм от обоих частей равенства (6).

 (7)

Для построения графика в логарифмических координатах предпочтительно по данным исходных таблиц строиться:

In yi	xi

4). Поленомальная аппроксимация

см вопрос № 16

Вопрос №17. Характеристики переменного гармонического тока и напряжения.

Переменным называется ток, сила которого I является функцией времени I(t).

Силой тока в общем случае называется производная:

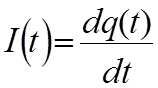, т.е. количество электрических зарядов протекающих через поперечное сечение проводника за единицу времени.

В случае, если протекающий заряд   пропорционален:

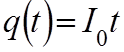, то производная примет вид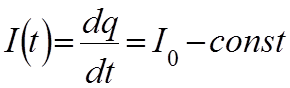

широкое применение на практике находит гармоническая зависимость переменного тока или напряжения от времени: