f(x) определяет количественные характеристики данного распределения или ее момент mi момент к – того порядка определяется по формуле:
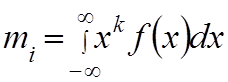 (2)
(2)
Момент случайной величины Xi определяемый
симметрично относительно начала координат называется начальным моментом.
Наиболее важным моментом является начальный момент первого порядка, которое
определяется математическое ожидание случайной величины х. 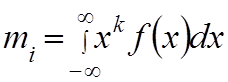 (4).
Кроме начальных моментов заданный закон распределения определяет центральные
моменты К – го порядка по формуле:
(4).
Кроме начальных моментов заданный закон распределения определяет центральные
моменты К – го порядка по формуле:
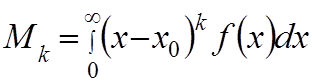 (3)
(3)
Х0 – центр распределения, который для нормального распределения совпадает математическим ожиданием случайной величины х и определяется по формуле:
х0=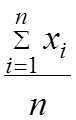 (средне арифметического) (4)
(средне арифметического) (4)
Само математическое ожидание также является случайной величиной и зависит как от измеренных значений, так и от числа измерений.
Считается, что центр значения ожидания имеет положительное значение. Наиболее важным является центральный момент второго порядка
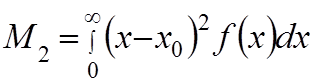 (5)
(5)
этот момент называется дисперсией Д случайной величины и характеризуется степенью отклонения измеренного Х от центра распределения, т.е. от математического ожидания.
Размерность Д равна размерности квадрата измеряемой величины Х. наряду с Д вводится квадратный корень из этой величины, т.е.:
![]() (6).
(6).
Выражение для σ в случае нормального распределения с использованием (5) и (6):
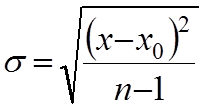
Вопрос №9. Закон распределения абсолютной погрешности прямого измерения.
Абсолютной погрешностью i-ого измерения в серии прямых измерений называется величина определяемая как разность между измеренным значением и средне арифметическим значением Х, которое для нормального закона распределения определяется по формуле:
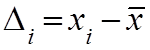 .
.
Причем Δi может появляться, как со знаком «+» так и со знаком «-»
Само арифметическое значение является величиной
случайной, зависящей от числа измерений в серии, степень разброса которой
характеризуется параметром ![]() определяемой по формуле:
определяемой по формуле:
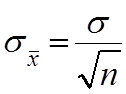 , т.е.
разброс средне арифметического относительно центра распределения в
, т.е.
разброс средне арифметического относительно центра распределения в ![]() раз
меньше, чем разброс относительно центра самой измеренной величины:
раз
меньше, чем разброс относительно центра самой измеренной величины:
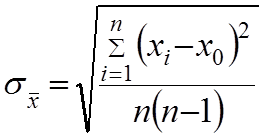
Абсолютная погрешность в серии прямых измерений также является случайной величиной подчиняется такому или иному закону распределения.
Нормальный закон для распределения абсолютной погрешности имеет вид:
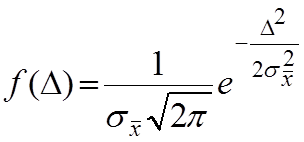 .
.
Если для самой случайной величины Х имеются некоторое ее наибольшая вероятность появления, то наибольшая вероятность значения абсолютной погрешности прямых измерений является ее значение равное 0.
![]() -
среднеарифметическое от средне квадратичного отклонения.
-
среднеарифметическое от средне квадратичного отклонения.
Вопрос №10. Интеграл вероятности. Доверительная вероятность и доверительный интервал.
Установлено, что при большом числе измерений в серии (большая выборка) закон распределения случайной величины, чаще всего сводится к нормальному или закону распределения Гаусса.
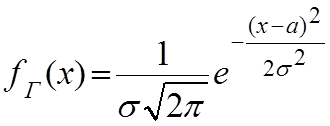 .(1)
.(1)
В частности можно предположить границы этого определенного интеграла, как 0 и ∞
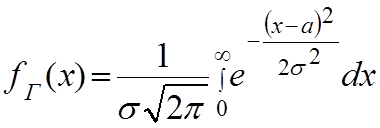 (2)
(2)
функция распределения f(x)
имеет вероятностный смысл, а любое значение f(x) распределяет
некоторое значение вероятности его появления. При этом вероятность появления
значения Х в интервале от Х ![]() до Х+dХ (dP).
до Х+dХ (dP).
![]() , (3)
тогда вероятность появления значения Х в некотором конечном интервале
ее изменения найдется по формуле.
, (3)
тогда вероятность появления значения Х в некотором конечном интервале
ее изменения найдется по формуле.
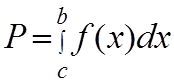 (4)
(4)
правая часть формулы называется интегралом вероятности, а левая доверительной вероятностью.
В теории вероятности максимальное значение вероятности не каждой случайной величины (ее достоверное значение) называется доверительным значением.
Вероятность того, что значение измеряемой величины Х лежит в пределах от 0 до ∞, является событие достоверное с вероятностью равной 1.
Математически это утверждение формируется в виде условия нормировки.
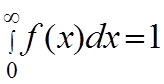 (5)
(5)
 поскольку функция f(x)
нормирована условием (5), то интеграл (4) должен быть <1.
поскольку функция f(x)
нормирована условием (5), то интеграл (4) должен быть <1.
Максимальное значение Δ (абсолютной погрешности) в серии прямых измерений соответственно с некоторой вероятностью ее появления (доверительной вероятности) называется границей доверительного интервала или доверительным интервалом.
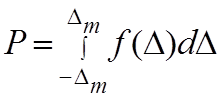 ,
(6)где Δi – определяет некоторое произвольное заданное
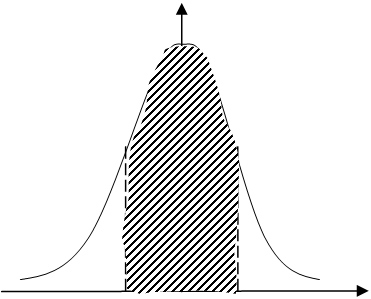
максимальное значение абсолютной погрешности измерений. Геометрически интеграл
(6) определяется как площадь криволинейной трапеции.
,
(6)где Δi – определяет некоторое произвольное заданное
максимальное значение абсолютной погрешности измерений. Геометрически интеграл
(6) определяется как площадь криволинейной трапеции.
Вопрос №11. Интеграл Лапласа. Формула доверительного интервала. Критерии выявления промахов.
Предположим, что число измерений в серии велико, при этом закон распределения самой случайной величины f(x), а также закон распределения f(Δ) – стремится к закону Гаусса.
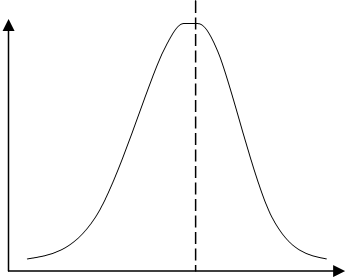
Поскольку кривая нормального распределения
симметричная интегралу 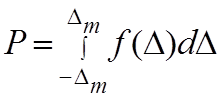 после подстановки в него f(x)
Гаусса можно представить в виде:
после подстановки в него f(x)
Гаусса можно представить в виде:
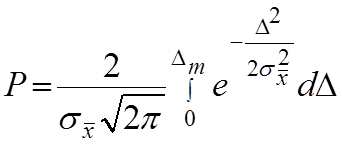 (1)
(1)
сделаем в интеграле (1) замену переменной, т.е. введем некоторую безразмерную величину:
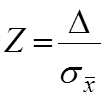 (2)
(2) 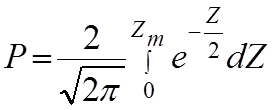
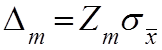 (3)
(3)
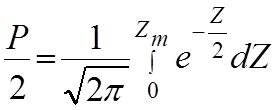
Вывод:
при нормальном законе распределения f(Δ) граница доверительного
интеграла, т.е. максимальное значение погрешности отклонения от среднего
арифметического определяется по формуле (3) при этом Zm находится по
таблицам интеграла Лапласа для заданного значения половины доверительной
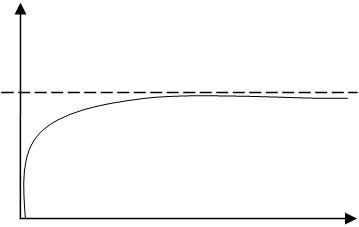
вероятности. Сам график интеграла Лапласа, т.е. функция 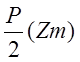 имеет
вид:
имеет
вид:
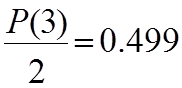 (4)
(4)
формула (4) показывает, что значение абсолютной
погрешности ![]() соответствует вероятности равной 0,499
соответствует вероятности равной 0,499
Интервал появления вероятности погрешности измерения Δ:
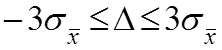 .
.
Вопрос № 12. Статическая обработка серии большой выборки прямого измерения.
При большой выборке (п ≥ 15), как показывает опыт, измеряемое значение Х обычно подчиняется нормальному закону распределения относительно некоторого максимума или моды функции распределения.
Мода измеряемой величины, как наибольшее вероятное ее значение является оценкой истинного значения величины Х или действительным ее значением в данной серии.
Однако, при обработке измерений, мода физической величины не определяется, а принимается, что при выполнения условия 1 (п ≥ 15) нормальным законом распределения выполняется.
За результат статическим обработками принимается нахождения математического ожидания физической величины для чего применяется следующий алгоритм вычислений.
1. Находится среднее арифметическое по серии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.