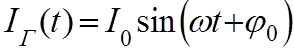
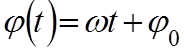
-
круговая или циклическая частота 
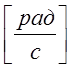
ν – физическая частота, измеряемая в Герцах [Гц]
Кроме гармонического тока (напряжения) часто
используются периодические или импульсный ток (напряжение).
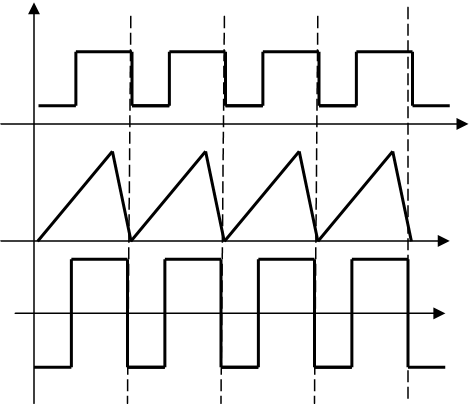
Ток, сила которого I есть некоторая
функция времени, называется переменным током. Аналогично можно внести понятие
переменного напряжения, когда разность потенциалов между точками цепи есть
функция времени.
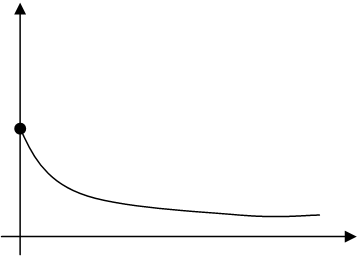
τ – время релаксации напряжения.
;
; 
, 
-
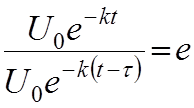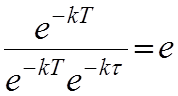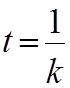
скважность импульсов (количество сигналов в единицу времени).
-
длина импульса.
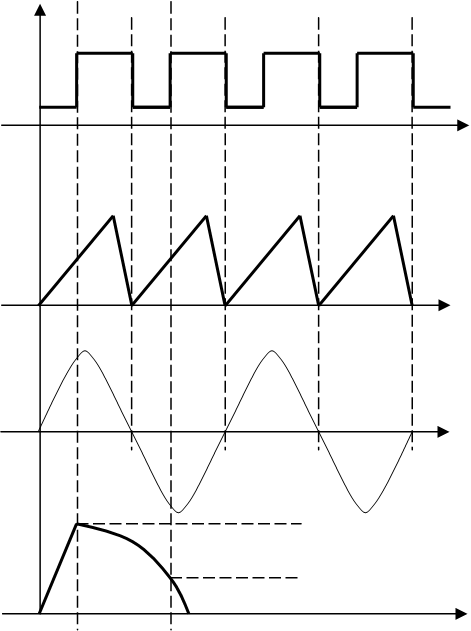
Периодический сигнал согласно теореме Фурье, можно представить в виде суммы гармоник (разложение функции в ряд Фурье или в интеграл Фурье). Число гармоник зависит от формы импульсов, в частности, для строго прямоугольного импульса п→∞.
Верхняя частота гармоники, т.е максимальное значение частоты гармоники обратно пропорционально времени нарастания переднего фронта.
Вопрос №18. Электромеханические преобразователи. Уравнения шкалы электроизмерительных аналоговых приборов.
Устройство преобразователей, позволяющее значение одной физической величины преобразовать в значение другой физической величины. В частности в виде некоторого эквивалентного электрического сигнала.
Такими преобразователями являются аналоговые стрелочные электроизмерительные приборы, которые преобразовывают энергию электромагнитного поля в механическую энергию поворота подвижной части прибора и жестко связанной с ней указательной стрелкой, которая в виде показания дает отклонение стрелки на некоторый угол α выраженный в градусах или делениях шкалы. Зная номинальное значение измеренной величины Yn и общее количество делений шкалы N можно найти цену деления шкалы:
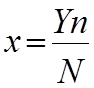
Величина обратная Х называется чувствительностью прибора:
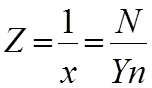
поворот подвижной части прибора на некоторый угол α связан с воздействием на нее вращающего момента М, которое согласно уравнению Лагранжа второго рода может быть найдено как производная электромагнитной энергии, преобразующей в данном устройстве по углу поворота стрелки указателя
В самом общем виде суммарная электроэнергия запишится:
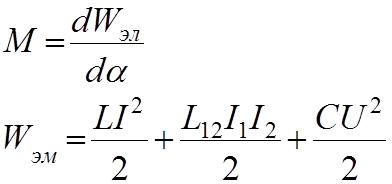
Имеется достаточно большое количество различных систем электроизмерительных приборов.
Наиболее употребляемые:
Магнитоэлектрическая
Электромагнитная
Электродинамическая
Электростатическая
Индукционная
Угловая и т.д.
В приборах того или иного типа преобладающим может являться то или иное слагаемое равенства (1). В этом случае другим слагаемым можно пренебречь.
Показано что вращающий момент М может зависеть от электрической величины I тремя способами:
1. 
(2)
2. 
(3)
3. 
(4)
Равенство (2) – магнитоэлектрические приборы (момент может быть пропорционален произведению двух электрических величин).
Равенство (3) реализуется в приборах электродинамической системы.
Равенство (4) – в приборах электромагнитных, электростатических и других системах.
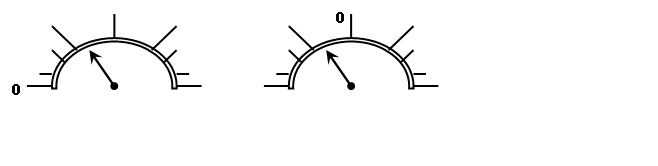
Шкала аналогового электроизмерительного прибора могут быть двух типов:
С началом шкалы у левого конца подвижная часть поворачивается всегда по часовой стрелки.
В зависимости от направления тока в измерительной катушке подвижная часть поворачивается как по часовой, так и против часовой.
Воздействие только одного момента на подвижную часть на позволяет провести измерения электрической величины Y поскольку стрелка прибора под воздействием сколь угодно малого момента М отклониться до упора. Поэтому наряду с вращательным моментом на подвижную часть действует еще и момент упругой возвращающей силой спиральной пружины. Обычно этот момент пропорционален углу закручивания.
При некотором значении электрических величины на входе прибора между моментами М и Мn устанавливается равновесие, т.е.
В зависимости от вида момента (2), (3) или (4) получаем то или иное уравнение шкалы.
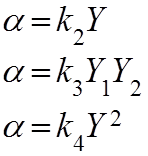
Вопрос №16. Полиномная аппроксимация. Метод наименьших квадратов.
Рассмотрим внешнею функцию аппроксимации описывает
лишь монотонные возрастания или убывание функции 
, не
позволяя выделить на поле точек экстремального их поведения
Полиномом п-ного порядка называется выражения
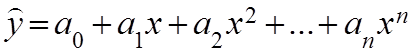
Рассмотрим полином второго порядка
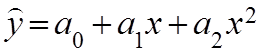
Задачей аппроксимации является нахождение коэффициента полинома, которую требуется провести таким образом, чтобы полином наилучшим образом проходил в близи всех эксперимент точек.
В качестве критерия оптимизации возьмем лианеризацию функционала F следующего вида.
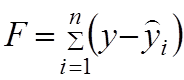(1)
п – общее количество экспериментальных точек
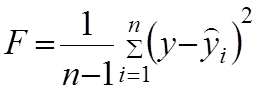
Функциональная F – есть дисперсия определения рассеяние экспериментальных точек от теоретической кривой.
Коэффициент полинома будем находить исходя из условия минимизации функционала F.
Проведем некоторое преобразование формулы (1).
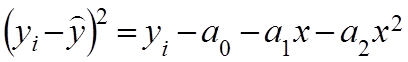
Введем переменные 
(2).
Тогда
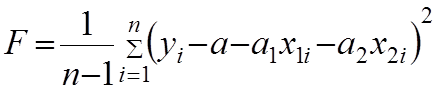(3)
Для нахождения коэффициента полинома условия минимизации (3) записываются в виде:
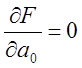
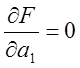
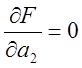
Полученная система уравнения позвонит найти искомый коэффициент полинома:
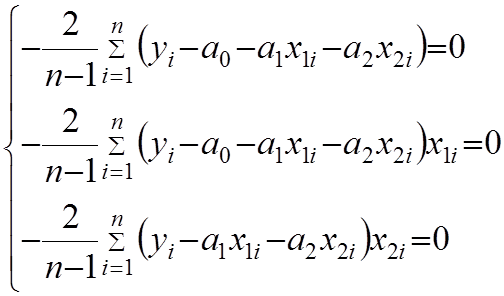(4)
Преобразует полученную систему:
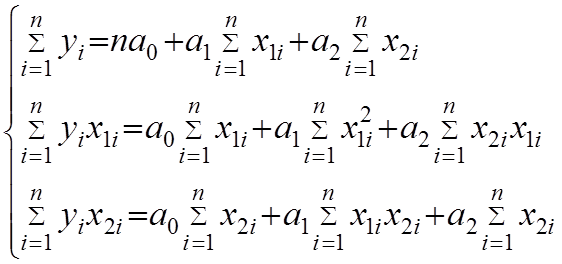(5)
Введем обозначения:
подсчитываются
по экспериментальным данным
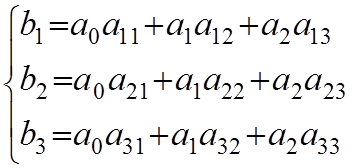(6)
Система линейных неоднородных уравнений.
Система (6) решает любым известным способом, например методом определителей (или Крамара).
, 
, 
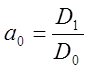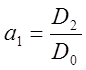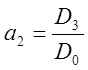
D0 основной определитель системы из коэффициентов неизвестных:
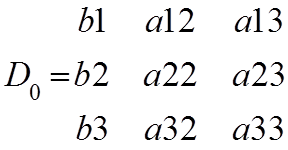
Вопрос №35. Мосты переменного тока. Условие равновесия.
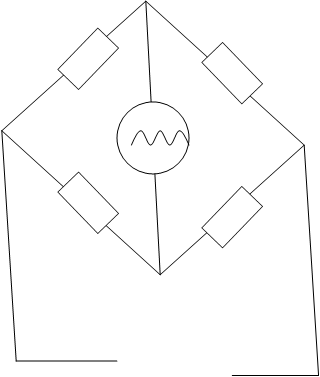Кроме активных сопр.
в качестве пассивных элементов электрических цепей исп. катушки индуктивности L и конденсаторы емкости C. Реактивные элементы L и C прим. в цепи переменного тока частоты w, причем реактивные сопр. этих
элементов опр. по формулам XC = 1/wC, XL = wL. Реальные реактивные элементы
конденсаторы и катушки кроме емкости и индуктивности хар. нек-рыми активными
сопр., наз. сопр. потерь. RL – активное сопр. провода, намотанного на катушку. Конденсаторы также
обл. нек-рым малым сопр. потерь., которое в зависимости от вел. вкл. в экв. сх.
конденсатора либо посл. (малые потери) либо пар. (большие потери), при этом
пластины C шунтируются акт. сопр.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.