Сумма квадратов решетчатой функции

Сумма квадратов решетчатой функции

Теорема 13. Если  является оригиналом, при чем если абсцисса абсолютной сходимости  D-преобразования этой функции отрицательна, то сумма квадратов значений функции  определяется по формуле:

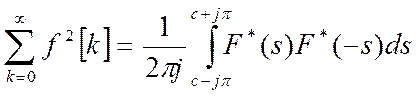  (1)

Где , при чем .

Доказательство:

Воспользуемся выражением:

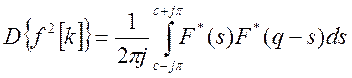  (2)

При этом должно выполняться неравенство:

Где  - показатель роста решетчатой функции . Абсцисса абсолютной сходимости этого D-преобразования, в соответствии с теоремой (7) удовлетворяет условию:

Выбирая , получаем, что . Следовательно, уравнение (2) является аналитической функцией правой полуплоскости и на мнимой оси.

Из непрерывности изображения в точке q=0 следует, что должно выполняться равенство:

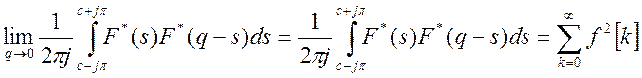   (3)