1.1.
Структурная чфема исследуемой автоматической системы с заданными значениями
параметров звена ![]() .
.
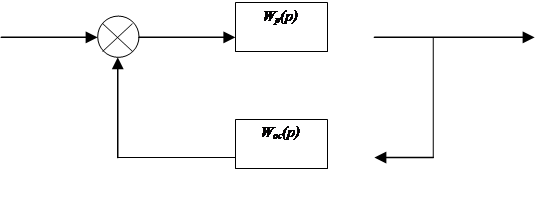
g y
±
Консервативное звено
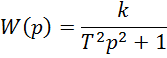
|
k |
T |
Вид обратной связи |
|
1 |
1 |
Гибкая ОС (идеальное дифференцирование) |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
g(t)xy(t)
(-1)
y1
Передаточная функция замкнутой автоматической системы имеет вид
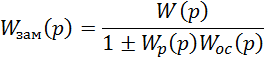
При отрицательной обратной связи
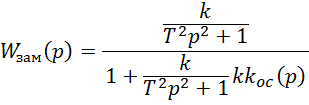
Упростим
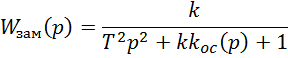
Видим что характер звена изменился
1.3.
Аналитические выражения, характеризующие процесс исследования и его результаты
замкнутой автоматической системы на устойчивость при охвате звена ![]() гибкой
отрицательной обратной связью.
гибкой
отрицательной обратной связью.
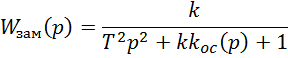
Т.к. ![]() ,
мы можем сделать вывод, что система устойчива.
,
мы можем сделать вывод, что система устойчива.
1.4. Аналитические
выражения, показывающие изменения параметров звена![]() при
охвате его гибкой положительной обратной связью.
при
охвате его гибкой положительной обратной связью.
Для
замкнутой автоматической системы, охваченной положительной обратной связью ![]() равно
равно
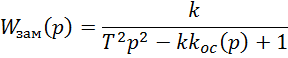
Видим что характер звена изменился.
1.5.
Аналитические выражения, характеризующие процесс исследования и его результаты
замкнутой автоматической системы на устойчивость при охвате звена ![]() гибкой
положительной обратной связью.
гибкой
положительной обратной связью.
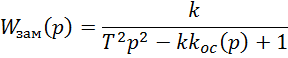
Т.к. ![]() ,
мы можем сделать вывод, что система неустойчива.
,
мы можем сделать вывод, что система неустойчива.
1.6. Соображения по выбору шага и интервала интегрирования.
Шаг интегрирования и величину интервала интегрирования выбираем из соображений наилучшего и рационального построения графиков.
1.7. Листинг фрагмента программы, относящегося к моделируемой автоматической системе.
Моделирование исходного звена
k11:=u2*dt;
k12:=(-(2*ksi/T)*u2-(1/(T*T))*u1+(k/(T*T))*g)*dt;
k21:=(u2+(k12/2))*dt;
k22:=(-(2*ksi/T)*(u2+k12/2)-(1/(T*T))*(u1+k11/2)+(k/(T*T))*g)*dt;
k31:=(u2+(k22/2))*dt;
k32:=(-(2*ksi/T)*(u2+k22/2)-(1/(T*T))*(u1+k21/2)+(k/(T*T))*g)*dt;
k41:=(u2+k32)*dt;
k42:=(-(2*ksi/T)*(u2+k32)-(1/(T*T))*(u1+k31)+(k/(T*T))*g)*dt;
u1:=u1+(k11+2*k21+2*k31+k41)/6;
u2:=u2+(k12+2*k22+2*k32+k42)/6;
u:=u1;
wu:=(u-upr)/dt;
upr:=u;
Моделирование замкнутой автоматической системы
k11:=y2*dt;
k12:=(-(2*ksi/T)*y2-(1/(T*T))*y1+(k/(T*T))*x)*dt;
k21:=(y2+(k12/2))*dt;
k22:=(-(2*ksi/T)*(y2+k12/2)-(1/(T*T))*(y1+k11/2)+(k/(T*T))*x)*dt;
k31:=(y2+(k22/2))*dt;
k32:=(-(2*ksi/T)*(y2+k22/2)-(1/(T*T))*(y1+k21/2)+(k/(T*T))*x)*dt;
k41:=(y2+k32)*dt;
k42:=(-(2*ksi/T)*(y2+k32)-(1/(T*T))*(y1+k31)+(k/(T*T))*x)*dt;
y1:=y1+(k11+2*k21+2*k31+k41)/6;
y2:=y2+(k12+2*k22+2*k32+k42)/6;
y:=y1;
x:=g+y3*kos;
y3:=(y-ypr)/dt;
ypr:=y;
1.8. Графики полученных функций.
Отрицательная связь ![]()
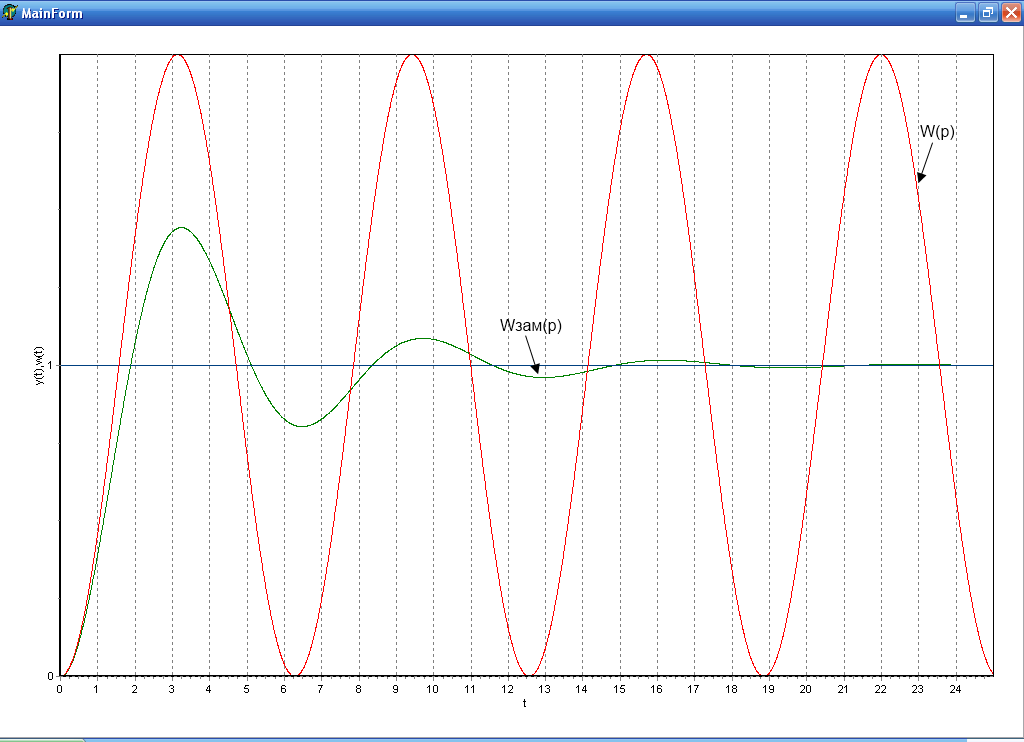
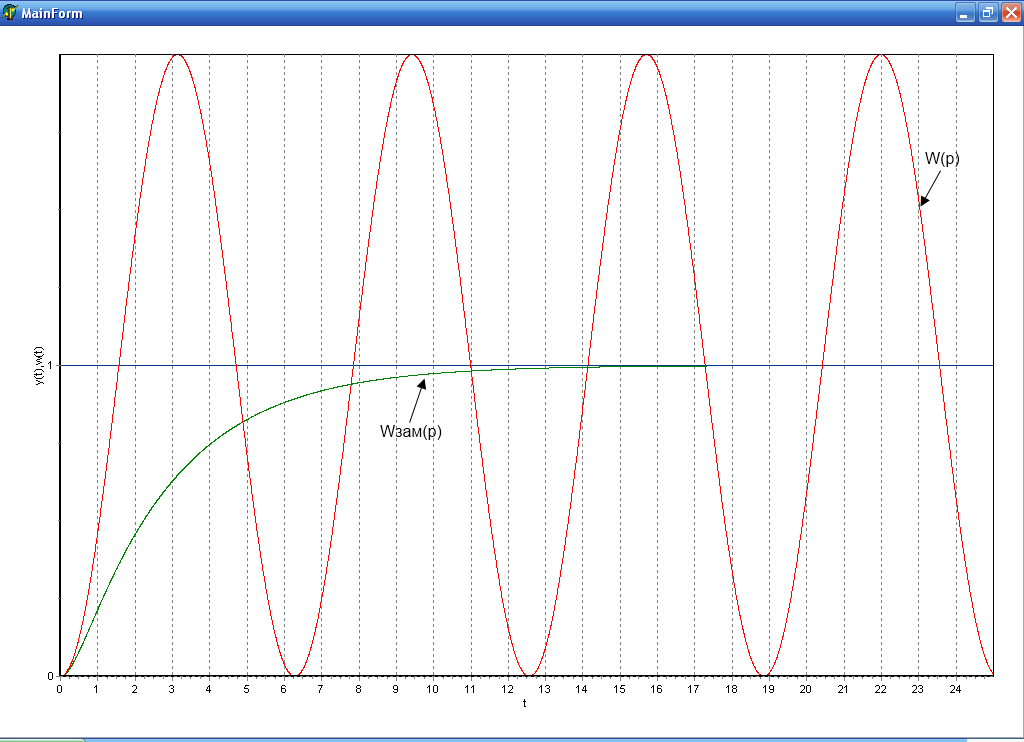
Отрицательная
связь ![]()
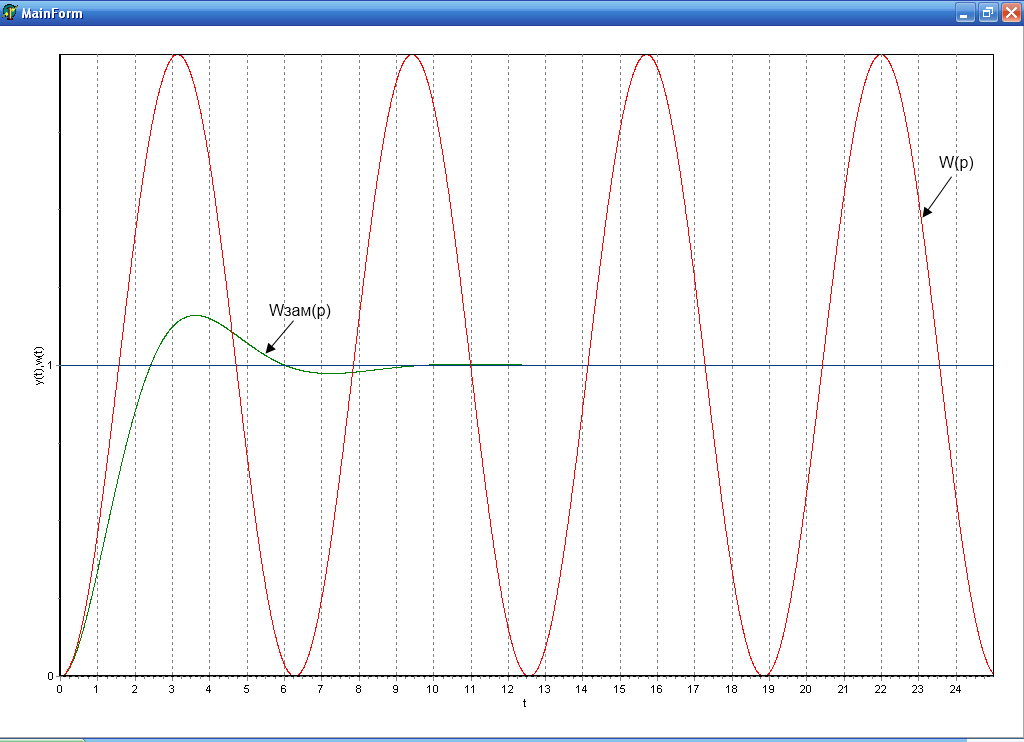
Отрицательная
связь ![]()
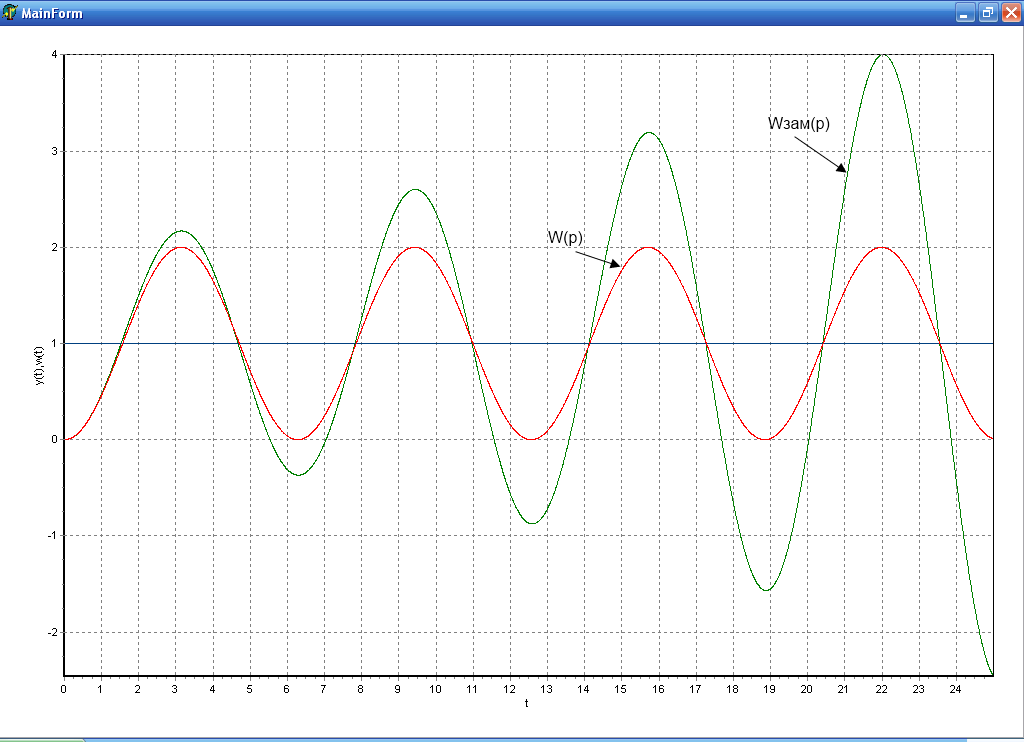 Положительная связь
Положительная связь ![]()
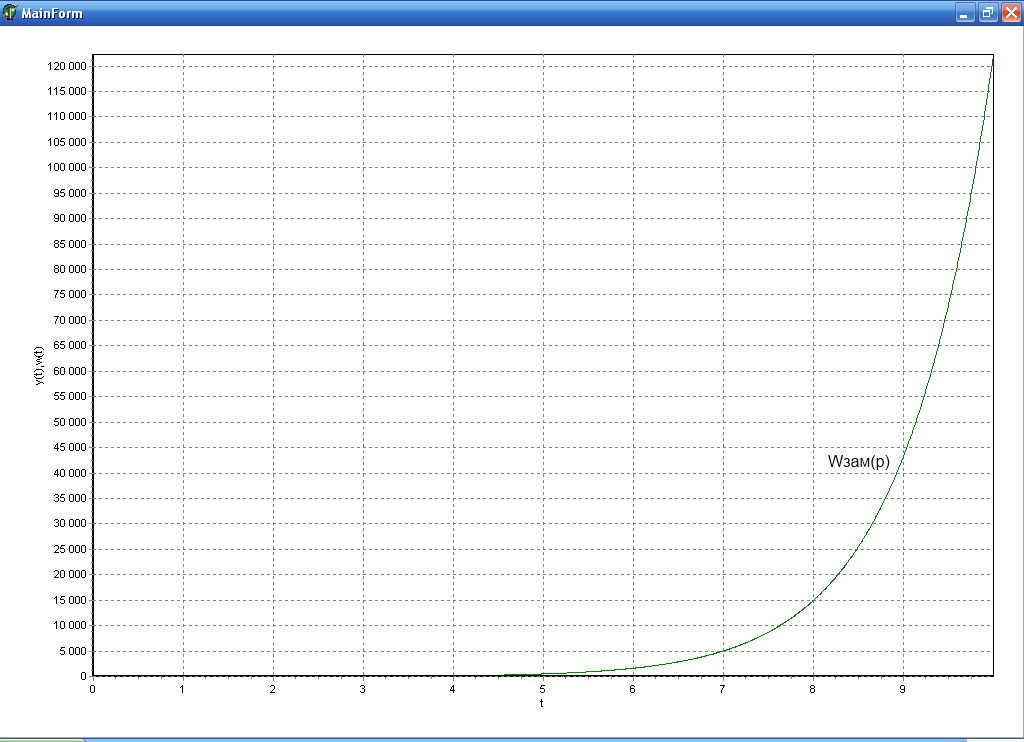
Положительная
связь ![]()
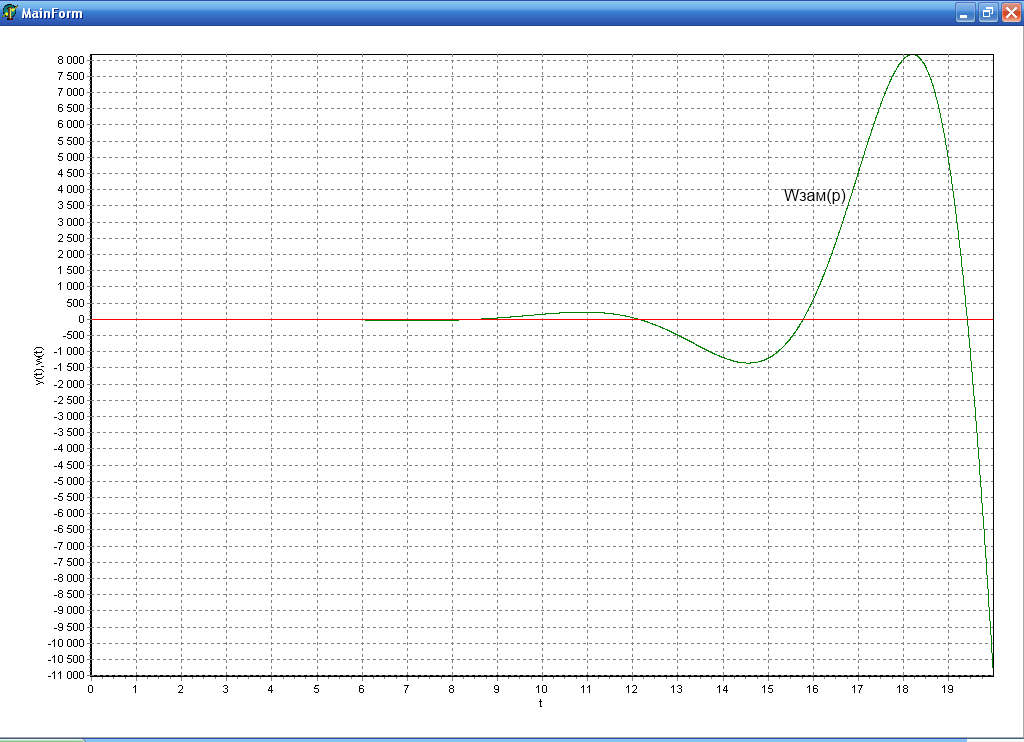 Положительная связь
Положительная связь ![]()
1.9. Доказательства изменения или характера звена или только его параметров при охвате ого обратной связью.
По полученным данным видим что при:
отрицательной связи, когда ![]() ,
звено стало колебательным
,
звено стало колебательным
отрицательной связи, когда ![]() ,
звено стало апериодическим первого рода
,
звено стало апериодическим первого рода
отрицательной связи, когда ![]() ,
звено стало колебательным
,
звено стало колебательным
положительной связи, когда ![]() ,
звено стало
,
звено стало
отрицательной связи, когда ![]() ,
звено стало
,
звено стало
отрицательной связи, когда ![]() ,
звено стало
,
звено стало
Список использованной литературы:
1. Куцый, А.С. Основы теории управления. Лабораторный практикум: лабораторные работы № 1-5 / Н.Н. Куцый. – Иркутск: ИрГУПС, 2008. – 72 с.
2. Теория систем автоматического регулирования / В. А. Бесекерский, Е. П.Попов. - Изд. 2-е , испр. и доп. - М. : Наука, 1972. - 767 с. : a-a-ил
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.