Статические и астатические САР

Лекция 6

(4 часа)

СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ САР

Понятие статических и астатических САР.

Порядок астатизма

Рассмотрим структурную схему САР, изображенную на рис.6.1.

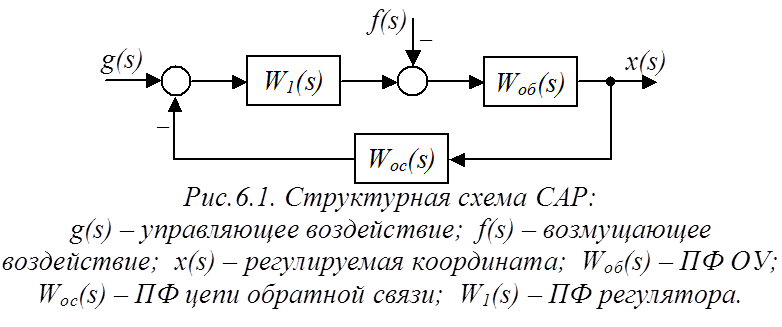
Задача – каким-то образом воспроизводить x(s) в соответствии с заданием g(s), уменьшив при этом (в идеале – исключив) влияние возмущения f(s) на регулируемую координату.

Напоминание. Статической называется система, в которой при наличии возмущения (нагрузки) присутствует ошибка регулирования, зависящая от его величины. В противном случае САР называется астатической. (Лекция 1)

Статизм и астатизм САР рассматривается раздельно применительно к управляющему g(s) и возмущающему f(s) воздействиям.

Для систем точного воспроизведения представляет интерес вопрос, является ли САР статической или астатической по управляющему воздействию. Если ошибка воспроизведения управляющего воздействия

         

в установившемся режиме (при ) равна нулю, то САР называется астатической по управляющему воздействию. В противном случае САР называется статической.

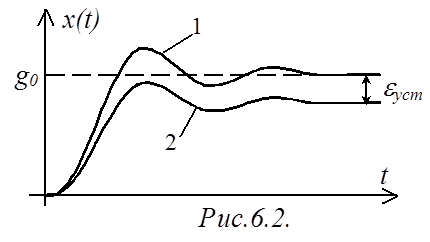Рассмотрим приведенное определение применительно к постоянному управляющему воздействию –  (рис.6.2): в случае 1  – следовательно, САР астатическая; в случае 2  отлична от нуля – САР статическая.

Учитывая, что в системах могут иметь место самые различные воздействия (см. рис. 4.4 – типовые воздействия), для астатических систем вводится понятие порядка астатизма  (1, 2, 3, …). Так, случаю 1 на рис.6.2 соответствует порядок астатизма по управляющему воздействию 1, случаю 2 – 0 (САР статическая).

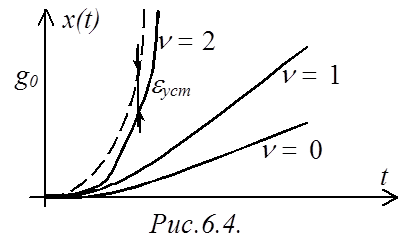
При линейно изменяющемся управляющем воздействии  (рис.6.3) (кривая 1-го порядка) ошибка в установившемся режиме будет равна нулю, если САР обладает порядком астатизма  по управляющему воздействию, при 1 в установившемся режиме будет иметь место постоянная ошибка , отличная от нуля. При 0 ошибка будет увеличиваться.

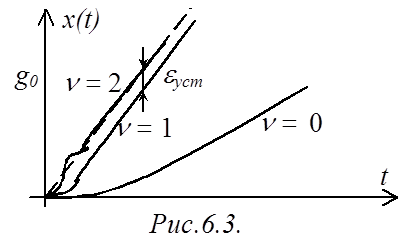Аналогично вводится понятие астатизма 3 по управляющему воздействию при квадратичном изменении управления  (рис.6.4) (кривая 2-го порядка) и т.д.

Вопросом статизма или астатизма по отношению к возмущающему воздействию интересуются в системах стабилизации. Если возмущающее воздействие оказывает влияние на регулируемую координату в установившемся режиме, то система называется статической по возмущающему воздействию, в противном случае – астатической.

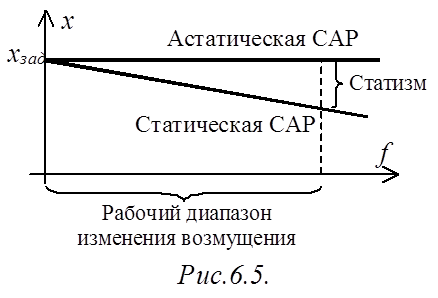Под статической характеристикой понимают зависимость  при постоянном управляющем воздействии  (рис.6.5). Для САР, астатической по возмущению, статическая характеристика представляет собой прямую линию, параллельную оси абсцисс.

В технических САР в роли возмущения обычно выступает нагрузка силового агрегата, которая может изменяться в заранее установленном диапазоне (рабочем). При этом максимальное значение возмущения обычно имеет место в нормальном (номинальном) режиме работы САР. Величина ошибка регулируемой координаты в номинальном режиме работы называется статизмом.

Примечание. Одна и та же САР может быть астатической по отношению к управляющему воздействию, но статичной по отношению к возмущающему, и наоборот. Поэтому при использовании терминов статическая или астатическая всегда следует добавлять, по отношению к какому воздействию термин применяется.

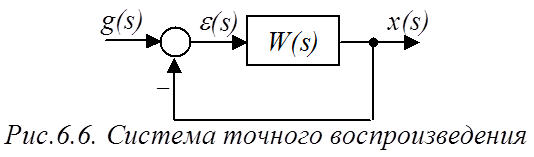
Системы точного воспроизведения

Обычно для таких систем ПФ цепи ОС равна единице:

          ,

т.е., вход равен выходу (рис.6.6).

Для определения установившейся ошибки может быть использована теорема о конечном значении (табл.2.2):

.

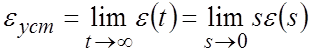Если окажется, что , САР является астатической, в противном случае – статической.

Представим ПФ разомкнутой САР (рис.6.6) в виде:

          ,

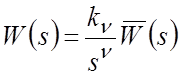где 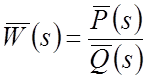 – нормированная ПФ разомкнутой САР, где .

       – порядок астатизма ПФ разомкнутой системы;

Система будет статической (), если интегрирующие звенья в чистом виде отсутствуют, либо все они скомпенсированы дифференцирующими. В противном случае САР будет астатической.

Для определения установившейся ошибки необходимо найти ПФ, считая входом управляющее воздействие g(s), а выходом – сигнал ошибки e(s):

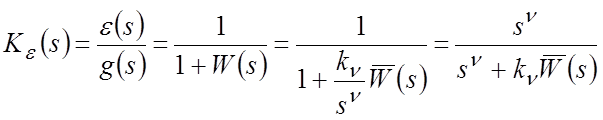           .                       (1)

Тогда установившаяся ошибка может быть вычислена следующим образом:

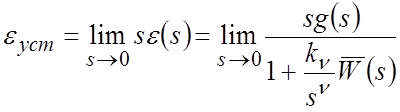              .                        (2)

В частном случае, при  (постоянное воздействие), когда , установившаяся ошибка будет равна:

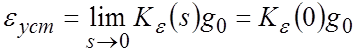              .                        (3)

Из (3) видно, что САР будет астатической, если . В противном случае САР будет статической. Но из (1) следует, что при  , а при  .

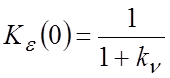Таким образом, если , то САР будет статической, и установившаяся ошибка будет обратно пропорциональна коэффициенту усиления  разомкнутой САР, сложенному с единицей.

Теоретически ошибку можно приблизить к нулю, устремляя  к бесконечности. Это положение реализуется в релейных САР, релейные элементы которых работают в скользящем режиме.

Система будет астатической, если порядок астатизма ПФ разомкнутой системы . Таким образом, в астатической САР всегда должны присутствовать интегрирующие звенья в чистом виде (хотя бы одно) – то есть, не должны компенсироваться дифференцирующими звеньями и не должны быть замкнутыми жесткими ОС.

Обратная связь является жесткой, если , если же , ОС является гибкой.

Если , то говорят, что замкнутая САР является астатической 1-го порядка, если  – астатической 2-го порядка и т.д.

Таким образом, порядок астатизма замкнутой САР по управляющему воздействию совпадает с порядком астатизма ПФ разомкнутой САР. Это видно из формулы (1).

Доказательство. Пусть имеется САР, ПФ которой по ошибке равна

                 .

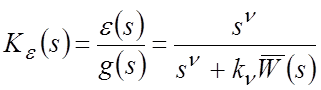Пусть к САР приложено управляющее воздействие (рис.4.4) , где  – порядок кривой.

Изображение управляющего воздействия по Лапласу (табл.2.1):

                 .

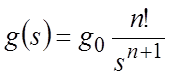Вычисляем установившуюся ошибку по (2):

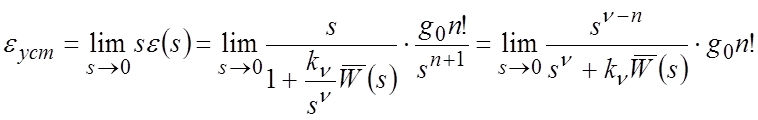
Из последнего выражения следует, что  при .

С помощью последней формулы можно определить установившуюся ошибку при любых  и . Так, частные случаи сведены в табл.6.1.

Табл.6.1. Установившиеся ошибки

Воздействие	0	1	2	3
Постоянное (n=0)		0	0	0
Линейное (n=1)			0	0
Парабола (n=2)				0

Таким образом, астатическая система 1-го порядка () отрабатывает линейно (n=1) возрастающий сигнал  – сигнал, изменяющийся с постоянной скоростью 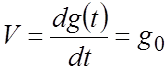, – с ошибкой, прямо пропорциональной скорости изменения задающего воздействия V, и обратно пропорциональной коэффициенту усиления разомкнутой САР. В установившемся режиме (рис.6.7) регулируемая координата x(t) изменяется также с постоянной скоростью V.

Величина, показывающая отношение скорости изменения регулируемой координаты к ошибке в установившемся режиме, называется добротностью САР по скорости, которая численно равна коэффициенту усиления  разомкнутой САР:

.

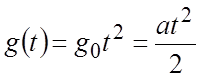Аналогичным образом, астатическая система 2-го порядка () отрабатывает параболически (n=2) возрастающий сигнал  – сигнал, изменяющийся с постоянным ускорением 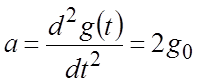, – с ошибкой, прямо пропорциональной ускорению a, и обратно пропорциональной коэффициенту усиления разомкнутой САР. В установившемся режиме (рис.6.8) регулируемая координата x(t) изменяется также с постоянным ускорением a.