Лекция №16
СИНТЕЗ ОПТИМАЛЬНОГО ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЯ. ТЕОРЕМА ОБ NИНТЕРВАЛАХ
Для получения предельного быстродействия (минимума времени переходного процесса) необходимо проектировать автоматические системы с учетом ограничений, наложенных на ее координаты, из условия минимума критерия качества (1.3). Системы управления называют оптимальными по быстродействию, если они обеспечивают минимум времени переходного процесса с учетом ограничений, наложенных на координаты управлений и выхода. Эти системы являются частным случаем оптимальных систем.
Пусть известна математическая модель объекта управления, например, в виде уравнений состояния типа
![]() , (5.10)
, (5.10)
где А – матрица размерности (![]() ); В – матрица размерности (
); В – матрица размерности (![]() ) при rкоординатах управления.
) при rкоординатах управления.
Требуется определить
допустимые управления u°(t) при наличии ограничений ![]() , переводящие
объект из заданного начального X(t0) в
заданное конечное состояние X(Т), из условия
минимума функционала
, переводящие
объект из заданного начального X(t0) в
заданное конечное состояние X(Т), из условия
минимума функционала
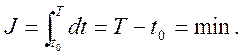 (5.11)
(5.11)
При этом координаты вектора
состояния X могут быть также ограничены: ![]() .
.
При решении задачи синтеза рассматривается оптимальное по быстродействию управление объектом либо без непосредственного использования координат вектора состояния X (разомкнутая система), либо с использованием координат вектора состояния X (замкнутая система). В связи с этим рассматриваемые системы делят на два основных типа: а) оптимальные по быстродействию разомкнутые системы; б) оптимальные по быстродействию замкнутые системы. Оба типа систем могут быть как одномерными, так и многомерными.
Синтез оптимальных по быстродействию систем производят методами теории оптимального управления. При этом основным методом является принцип максимума Понтрягина (см. гл. 3).
При решении задачи синтеза составляют функцию Гамильтона вида (3.135) и на основании условия (3.136) находят закон управления (3.137).
Запишем основные выражения, необходимые при решении задачи синтеза по принципу максимума (см. §3.6).: функция Гамильтона
![]() ; (5.12)
; (5.12)
уравнение вектора вспомогательных переменных
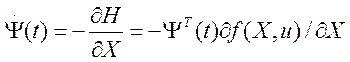 ; (5.13)
; (5.13)
условие максимума функции Гамильтона
![]() ;
; ![]() , (5.14)
, (5.14)
на основании которого находится закон
оптимальных управлений при ![]() [cм.(3.137)]:
[cм.(3.137)]:
![]() , (5.15)
, (5.15)
где I – единичная матрица;
![]() . (5-16)
. (5-16)
Таким образом, уравнения
(5.10), (5.13) и управления (5.15) составляют систему 2п + rуравнений вариационной задачи синтеза
оптимальных по быстродействию управлений с 2п + rнеизвестными. Все эти неизвестные могут
быть определены, если известны начальные условия xi(t0) и
yi(t). Сложность задачи состоит в том, что известны только начальные
значения координат состояния объекта xi(t0) и
неизвестны начальные значения yi(t). Так как
нет аналитических способов определения yi(t0) в явном виде, то для их нахождения
используют метод последовательных приближений (метод итераций) от некоторого
исходного набора значений ![]() –начальное
приближение – к окончательной совокупности
–начальное
приближение – к окончательной совокупности ![]() ,
соответствующей решению оптимальной задачи. Один из способов такого решения
состоит в следующем [12]. Взяв произвольно значения
,
соответствующей решению оптимальной задачи. Один из способов такого решения
состоит в следующем [12]. Взяв произвольно значения ![]() , найдем
соответствующие им управления
, найдем
соответствующие им управления ![]() и
траектории
и
траектории ![]() .
Если полученные
.
Если полученные ![]() совпадают
с заданными конечными значениями при
совпадают
с заданными конечными значениями при ![]() т. е. вектор
состояния Х°(Т) равен заданному вектору конечного состояния X (Т), то
начальные значения
т. е. вектор
состояния Х°(Т) равен заданному вектору конечного состояния X (Т), то
начальные значения ![]() выбраны
правильно и задача решена. В том случае, когда траектории
выбраны
правильно и задача решена. В том случае, когда траектории ![]() не проходят через заданные конечные значения хi(Т), необходимо выбрать другие значения
не проходят через заданные конечные значения хi(Т), необходимо выбрать другие значения ![]() и повторить решение задачи.
и повторить решение задачи.
Однако при оптимизации
некоторых объектов решение задачи синтеза может быть проще указанного, так как
в ряде случаев не требуется определять полностью вспомогательные функции ![]() , а достаточно только
знать моменты
, а достаточно только
знать моменты ![]() изменения знака Ни,
в результате чего на основании (5.15) и (5.16) может быть составлен закон
релейного управления:
изменения знака Ни,
в результате чего на основании (5.15) и (5.16) может быть составлен закон
релейного управления:
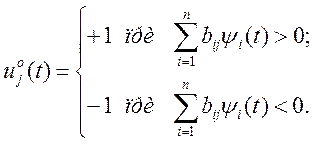 (5.17)
(5.17)
В связи с этим, применяя принцип максимума, рассмотрим теорему «об п интервалах». Пусть математическая модель одномерного объекта задана уравнениями состояния
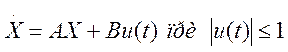 . (5.18)
. (5.18)
Составим функцию Гамильтона для неклассической вариационной задачи оптимального по быстродействию управления
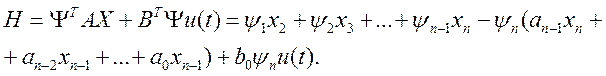 (5-19)
(5-19)
Так как от управления и(t) зависит только последнее слагаемое, то в соответствии с (5.14) функция Гамильтона имеет максимум, когда
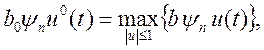
откуда следует закон оптимального по быстродействию управления (5.15)
и° (t) = 1 × sign [yn(t)]. (5.20)
При этом функция и°(t) принимает два значения:
![]()
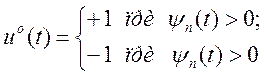 (5.21)
(5.21)
и меняет знак столько раз, сколько кривая ![]() пересекает ось времени.
пересекает ось времени.
Для нахождения
вспомогательной переменной ![]() составим
сопряженные уравнения Гамильтона:
составим
сопряженные уравнения Гамильтона:
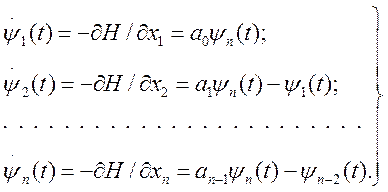 (5.22)
(5.22)
Приведем систему уравнений (5.22) к одному уравнению. Для этого вычтем из первого уравнения системы (5.22) все остальные, продифференцировав предварительно второе уравнение один раз и умножив на (–1)1, третье – два раза и умножив на (–1)2 и т. д. до последнего, которое дифференцируем (п – 1) раз и умножаем на (–1)(n-1). В результате этого после группирования получим
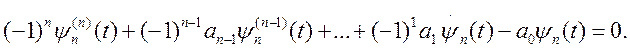 (5.23)
(5.23)
Предполагаем, что собственные числа матрицы А в (5.18) являются различными вещественными, тогда корни уравнения (5.23) также будут вещественными различными числами piВ этом случае
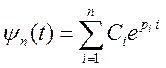 (5.24)
(5.24)
Функция ![]() , определяемая суммой
экспонент с вещественными показателями степени, изменит знак не более (п –
1) раз, поэтому управление (5.20) имеет не более п интервалов постоянных
значений
, определяемая суммой
экспонент с вещественными показателями степени, изменит знак не более (п –
1) раз, поэтому управление (5.20) имеет не более п интервалов постоянных
значений ![]() . Таким образом, доказана теорема «об
п интервалах»: Если объект управления описывается линейным
дифференциальным уравнением п-го порядка с постоянными
коэффициентами и корни его характеристического уравнения различные,
отрицательные или нулевые, то для оптимального по быстродействию управления
необходимо и достаточно не более п интервалов максимального значения
управления |и| = Umax, а знаки на
интервалах должны чередоваться (п – 1) раз.
. Таким образом, доказана теорема «об
п интервалах»: Если объект управления описывается линейным
дифференциальным уравнением п-го порядка с постоянными
коэффициентами и корни его характеристического уравнения различные,
отрицательные или нулевые, то для оптимального по быстродействию управления
необходимо и достаточно не более п интервалов максимального значения
управления |и| = Umax, а знаки на
интервалах должны чередоваться (п – 1) раз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.