Лекция 9
СИНТЕЗ САР
Различают синтез "в большом" и "в малом".
При синтезе "в большом" обычно подлежит определению передаточная функция замкнутой САР, наилучшей в каком-то смысле слова (т.е. обеспечивающей экстремальное значение какого-либо показателя качества). Задача это весьма сложная и не всегда приводит к желаемому результату.
При синтезе "в малом" подлежат определению передаточные функции корректирующих звеньев (регуляторов) при которых САР отвечает заданным показателям качества.
Различают последовательные и параллельные корректирующие звенья, и, следовательно, САР с последовательной и параллельной коррекцией.
Синтез систем с последовательной коррекцией
Содержание синтеза последовательных корректирующих звеньев
Обобщенная структурная схема САР с последовательной коррекцией представлена на рис.9.1. Помимо неизменяемой части САР (объекта регулирования) присутствует часть, параметры которой можно выбрать, – корректирующее звено.
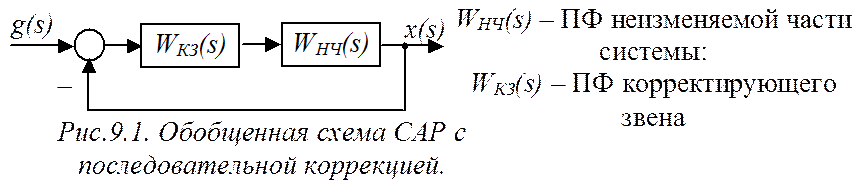
Частотная характеристика разомкнутой системы:
![]()
ЛАЧХ разомкнутой системы:
![]() .
.
Назовем систему, которая обеспечивает заданные динамические и статические свойства, – желаемой, а ЛАЧХ желаемой системы в разомкнутом состоянии – желаемой ЛАЧХ:
![]() .
.
Проектируемая система будет удовлетворять заданным требованиям, если ЛАЧХ разомкнутой системы будет равна желаемой ЛАЧХ:
![]() .
.
Следовательно, желаемую САР можно синтезировать за счет выбора соответствующей ПФ корректирующего звена.
Синтез системы с последовательной коррекцией включает:
1) Синтез желаемой ЛАЧХ Lж(w);
2) Определение ЛАЧХ корректирующего звена LКЗ(w) и его ПФ WКЗ(s);
3) Реализацию некоторого устройства с ПФ WКЗ(s).
Синтез желаемой ЛАЧХ, в свою очередь, включает в себя три этапа:
· синтез низкочастотной ЛАЧХ;
· синтез среднечастотной ЛАЧХ;
· синтез высокочастотной ЛАЧХ.
Синтез низкочастотной ЛАЧХ
Низкочастотная ЛАЧХ в основном определяет точность работы САР в установившихся режимах. Таким образом, ее синтез может быть выполнен на основании требований к системе по точности.
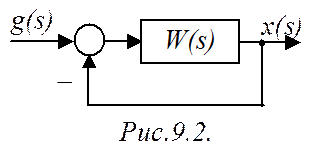 Предположим, что речь идет о статической САР
(порядок астатизма разомкнутой системы n=0). Тогда
Предположим, что речь идет о статической САР
(порядок астатизма разомкнутой системы n=0). Тогда
![]() ,
,
где
![]() – нормированная ПФ.
– нормированная ПФ.
Установившаяся ошибка в статической системе при
отработке скачкообразного воздействия ![]() :
:
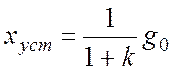 .
.
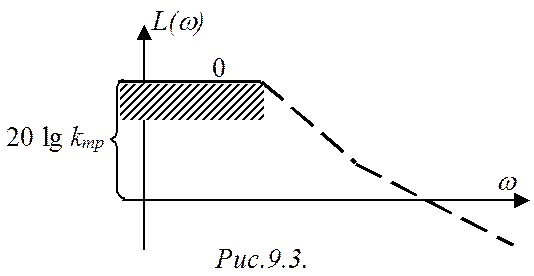 Отсюда с учетом требований системы по точности можно определить требуемое
значение коэффициента усиления kтр. Синтезированная низкочастотная ЛАЧХ в этом случае имеет
наклон 0, как показано на рис.9.3.
Отсюда с учетом требований системы по точности можно определить требуемое
значение коэффициента усиления kтр. Синтезированная низкочастотная ЛАЧХ в этом случае имеет
наклон 0, как показано на рис.9.3.
Разумеется, что низкочастотная ЛАЧХ синтезируемой САР не должна заходить в запретную зону (заштрихована), поскольку при этом k<kтр, и ошибка будет превышать требуемое значение.
Рассмотрим астатическую САР 1-го порядка (n=1).
В этом случае задают требуемое значение коэффициента ошибки с1, и определяют требуемую добротность САР по скорости, равную коэффициенту усиления разомкнутой системы:

![]() .
.
Зная
![]() , можно синтезировать низкочастотный
участок ЛАЧХ (рис.9.4). Низкочастотная ЛАЧХ синтезируемой САР не должна
заходить в запретную зону (заштрихована), поскольку в этом случае коэффициент
ошибки с1 будет превышать заданное значение.
, можно синтезировать низкочастотный
участок ЛАЧХ (рис.9.4). Низкочастотная ЛАЧХ синтезируемой САР не должна
заходить в запретную зону (заштрихована), поскольку в этом случае коэффициент
ошибки с1 будет превышать заданное значение.
В то же время такой синтез не контролирует значения коэффициента ошибки с2 (т.е. неизвестно, как система будет отрабатывать воздействие 2-го порядка). Для таких случаев по дополнительно заданному коэффициенту ошибки с2 определяют первую частоту w1, при которой происходит изменение наклона низкочастотной ЛАЧХ (рис. 9.5, 9.6).
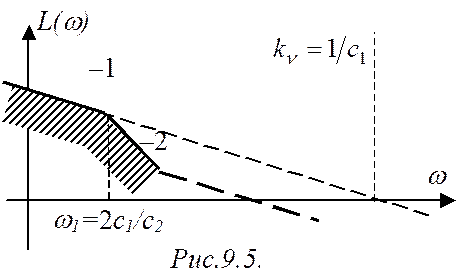
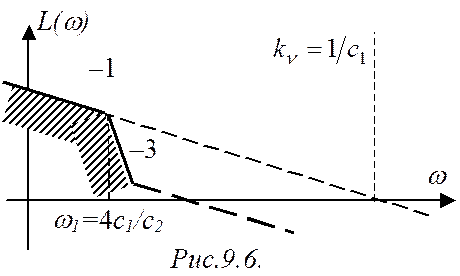
Рассмотрим астатическую САР 2-го порядка (n=2).
В этом случае задают требуемое значение коэффициента ошибки с2, и определяют требуемую добротность САР по ускорению, равную коэффициенту усиления разомкнутой системы:
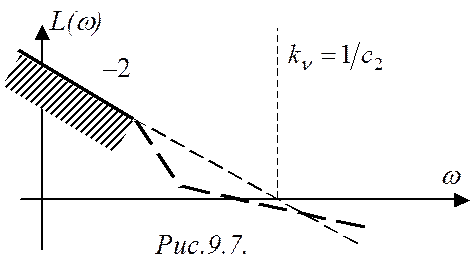
![]() .
.
Зная ![]() , можно
синтезировать низкочастотный участок ЛАЧХ (рис.9.7). Низкочастотная ЛАЧХ синтезируемой
САР не должна заходить в запретную зону, поскольку в этом случае коэффициент
ошибки с2 будет превышать заданное значение.
, можно
синтезировать низкочастотный участок ЛАЧХ (рис.9.7). Низкочастотная ЛАЧХ синтезируемой
САР не должна заходить в запретную зону, поскольку в этом случае коэффициент
ошибки с2 будет превышать заданное значение.
Синтез среднечастотной ЛАЧХ
Среднечастотный участок ЛАЧХ (участок в области частоты среза) определяет как быстродействие, так и колебательность САР. Любая система для обеспечения приемлемых показателей качества должна иметь ЛАЧХ, которая пересекает ось частот при наклоне "–1" (–20 дБ/дек).
Исходными данными для синтеза среднечастотной ЛАЧХ являются желаемые параметры: время первого согласования tc, время достижения максимального значения tm, время регулирования tр и перерегулирование s.
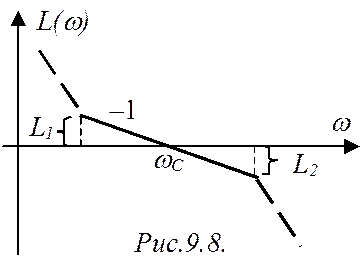 Замечено, что чем длиннее среднечастотный участок ЛАЧХ
с наклоном "–1", тем меньше перерегулирование s при прочих равных условиях. Обычно длину среднечастотного участка
ЛАЧХ выражают через координаты L1 и L2
(рис.9.8). Часто стремятся, чтобы
Замечено, что чем длиннее среднечастотный участок ЛАЧХ
с наклоном "–1", тем меньше перерегулирование s при прочих равных условиях. Обычно длину среднечастотного участка
ЛАЧХ выражают через координаты L1 и L2
(рис.9.8). Часто стремятся, чтобы
L1 = L2 = L,
Причем L оказывается численно равным запасу устойчивости по амплитуде.
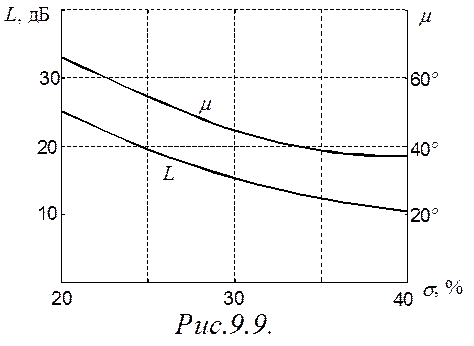
Имеются графики зависимостей L=f(s) и m=f(s) [1], представленные на рис.9.9. Используя эти зависимости, при заданном значении перерегулирования s можно выбрать требуемые значения запаса устойчивости по амплитуде и по фазе.
 Если задано значение tm,
то можно приближенно определить значение частоты среза:
Если задано значение tm,
то можно приближенно определить значение частоты среза:
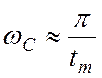 .
.
Если заданы только tС и s, не задано, то можно предварительно воспользоваться зависимостью tC/tm=f(s) [3], показанной на рис.9.10, и получить
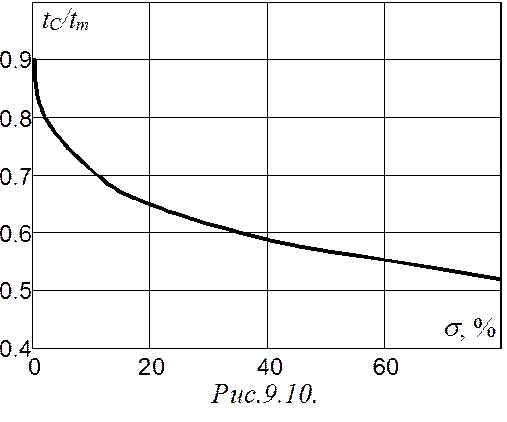 tC/tm=число,
tC/tm=число,
и из этого соотношения определить tm.
Если же заданы только tp и s, то из соотношения
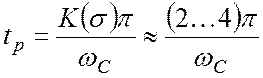
можно определить значение частоты среза:
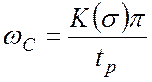 .
.
Синтез высокочастотной ЛАЧХ
В силу того, что высокочастотный участок ЛАЧХ не оказывает влияния на показатели качества работы САР, его вид принципиально может быть выбран любым. Но обычно высокочастотный участок ЛАЧХ принимают таким, при котором корректирующее звено будет реализовано наиболее просто.
Синтез корректирующего звена
Если известны желаемая ЛАЧХ и ЛАЧХ неизменяемой части САР, то ЛАЧХ корректирующего звена находят из соотношения:
![]() .
.
Например, если имеем заданные ЛАЧХ, изображенные графически (рис.9.11), то ЛАЧХ последовательного корректирующего звена можно получить путем геометрического вычитания.
Имея ЛАЧХ корректирующего звена, можно определить его передаточную функцию:
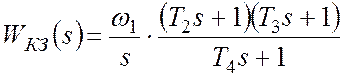 .
.
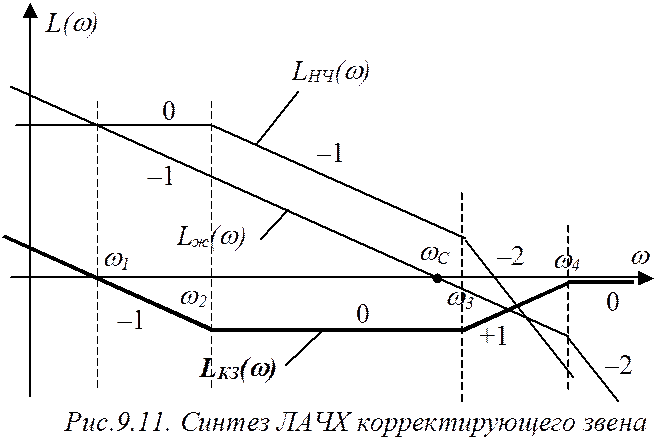 Из рассмотренного примера видно, что ПФ корректирующего
звена и, следовательно, его реализация будет проще, если желаемая ЛАЧХ в области
высоких частот по характеру совпадает с ЛАЧХ неизменяемой части.
Из рассмотренного примера видно, что ПФ корректирующего
звена и, следовательно, его реализация будет проще, если желаемая ЛАЧХ в области
высоких частот по характеру совпадает с ЛАЧХ неизменяемой части.
Например, если в рассмотренном примере (рис.9.11) в желаемой ЛАЧХ сделать наклон "–2" после w3, то корректирующее звено будет иметь более простую ПФ:
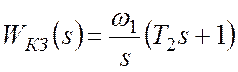 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.