Смещение комплексного переменного в изображении по Лапласу.
Теорема 3. Смещение
аргумента q изображения по Лапласу 
на произвольную комплексную величину 
соответствующую смещению на ту же
величину аргумента q изображения 
и умножению последнего на
экспоненциальную функцию в соответствии с равенством:
(1)
Где 
.
Доказательство:
Применим 
-
преобразование к смещенной функции 
. Это - преобразование определяется по
формуле:
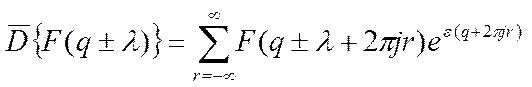
Если теперь умножим и разделим
обе части на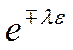 
, то получим:
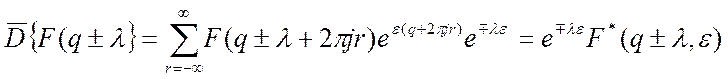
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
