Лекция №17
СИНТЕЗ ОПТИМАЛЬНЫХ ПО БЫСТРОДЕЙСТВИЮ ЛИНЕЙНЫХ СИСТЕМ
При синтезе оптимальных по быстродействию систем обычно требуется определить либо закон управления типа (5.15) в функции времени, либо законы управления типа (3.138) или (3.141). В первом случае управление и°(t) обеспечивает оптимальные по быстродействию процессы при разомкнутом', управлении объектом, а во втором случае управление и0(X) или и0(Е) определяет структуру оптимального регулятора, где Е – вектор координат ошибок е1(t), e2 (t), ..., еп (t).
Основная задача при
определении алгоритмов оптимальных управлений и°(t) состоит в нахождении моментов переключения реле ![]() , (
, (![]() 1,
2, ..., п), так как на основании теоремы об п интервалах
управление является релейным с числом интервалов не более п, на которых и°(t) = ±Umax, и имеет место (п – 1)
переключение реле.
1,
2, ..., п), так как на основании теоремы об п интервалах
управление является релейным с числом интервалов не более п, на которых и°(t) = ±Umax, и имеет место (п – 1)
переключение реле.
Определение моментов переключения tvв общем случае является сложной задачей. Моменты переключения сигнала управления со значения +Umaxна значение –Umaxможно рассчитать различными методами, например методами «сшивания» решений [2].
Метод «сшивания» решений. Пусть дифференциальное уравнение одномерного линейного объекта при отсутствии ограничений координат выхода и без учета возмущающих воздействий имеет вид
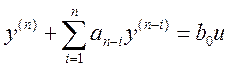 . (5-25)
. (5-25)
Тогда для определения tvможно применить способ «сшивания» решений уравнения (5.25) со знакопеременной правой частью и (t) = ± Umax.
Запишем известное решение уравнения (5.25) при различных вещественных корнях характеристического уравнения объекта на интервалах:
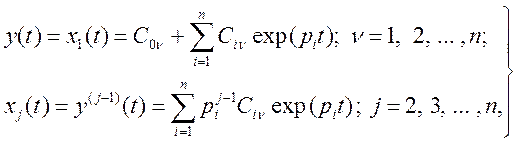 (5.26)
(5.26)
где Cov определяется на интервалах u значением и(t) и заданным конечным значением координаты выхода; Civ– постоянные интегрирования, зависящие от заданного вектора начального и конечного состояний X(t0) и X(Т); рi ≠ 0 – корни характеристического уравнения объекта (для устойчивого объекта pi< 0).
Рассмотрим процесс перевода
объекта из заданного начального состояния t0= 0, при котором 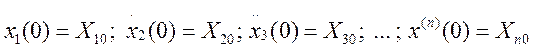 , в заданное
конечное установившееся состояние
, в заданное
конечное установившееся состояние ![]()
Пусть начальное управление ![]() тогда на конце первого интервала
управления
тогда на конце первого интервала
управления
![]() (5.27)
(5.27)
После переключения реле значение координаты выхода
![]() . (5.28)
. (5.28)
Приравнивая правые части (осуществляя «сшивание» решений), получим
![]() (5.29)
(5.29)
Аналогично (5.27)–(5.29)
необходимо записать выражения для 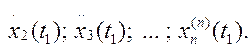 В результате
получим n уравнений с 2n неизвестными постоянными интегрирования Ci1и Ci2. Постоянные Ci1определяются
начальными условиями при t= 0,
поэтому из уравнений для начала первого интервала запишем
В результате
получим n уравнений с 2n неизвестными постоянными интегрирования Ci1и Ci2. Постоянные Ci1определяются
начальными условиями при t= 0,
поэтому из уравнений для начала первого интервала запишем
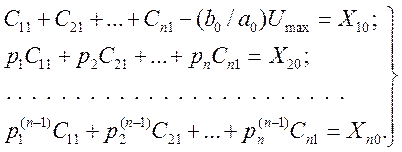 (5.30)
(5.30)
Уравнения (5.30) позволяют определить постоянные Сi1, подставив которые в уравнения, записанные после «сшивания» решений в момент первого переключения реле, получим п уравнений для определения постоянных Ci2, которые выражаются через моменты первого переключения t1.
Аналогично продолжаем решение до последнего интервала, для которого постоянные интегрирования Cinбудут выражены через tn=Т. В результате исключим постоянные интегрирования и получим n трансцендентных уравнений с п неизвестными tv. Решение этих уравнений в общем случае является очень трудоемким и производится обычно на ЦВМ [2].
В случае, когда уравнение объекта (5.25) имеет п нулевых корней, моменты переключения [17]
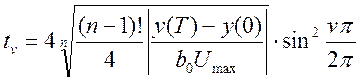 . (5.31)
. (5.31)
На основании выражения (5.31) можно сделать вывод, что моменты переключений tvзависят от начальных и конечных значений координаты выхода объекта, а также от величины Umax.
Если время переходного процесса
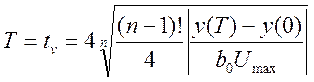 ,(5.32)
,(5.32)
то моменты tv могут быть определены графически (рис. 5.5) путем деления полуокружности, диаметр которой равен T, на п равных частей и проектирования полученных точек на ось абсцисс [17]. На рис. 5.5 принято п= 4.
Особое значение при расчете моментов переключения реле tvимеет выбор знака сигнала управления на первом интервале и1°. Если начальное и конечное состояния объекта установившиеся, то [17]
![]() (5.33)
(5.33)
В общем случае выражение для и1° будет более сложным, чем (5.33).
Методы математического программирования. Рассмотрим применение методов математического программирования для определения длительности интервалов управления по уравнениям переходных состояний объекта. Пусть одномерный объект задан уравнениями состояния
![]()
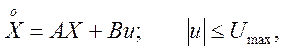 (5.34)
(5.34)
которым соответствуют уравнения переходных состояний [см. (2.11)]:
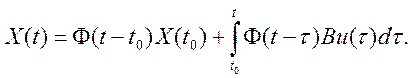 (5.35)
(5.35)
Разделим интервал времени [t0, tK] на п интервалов Dt1:
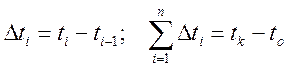 (5.36)
(5.36)
С учетом (5.36) и |u(Dti)| = Umax = const вместо (5.35) запишем уравнения переходных состояний на интервалах управлений [ti, ti–1].
![]() (5.37)
(5.37)
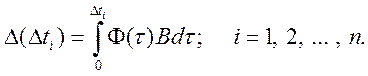 (5.38)
(5.38)
Тогда задача синтеза оптимального управления и0(t), обеспечивающего минимум времени переходного процесса (оптимальное быстродействие), может быть сформулирована как задача математического программирования типа (3.148) для значения вектора координат состояния на последнем интервале X(Dtn) = X(tк):
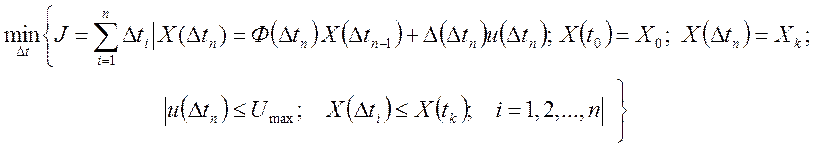 (5.39)
(5.39)
|
Рис. 5.5 |
Рис. 5.6 |
Чтобы решить задачу (5.39),
необходимо применить методы нелинейного программирования, так как уравнения
(5.38) являются нелинейными относительно искомых Dti. При этом 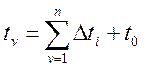 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.