Связь между D-преобразованием и преобразованием Лапласа

Связь между D-преобразованием и преобразованием Лапласа. - преобразование.

Установим связь между преобразованием Лапласа обычной функции и D-преобразованием соответствующих ей решетчатых функций. Прежде всего введем новую переменную 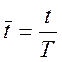, где T – период дискретности решетчатой функции.

Введем обозначение:

Преобразование Лапласа для  определяется следующим образом:

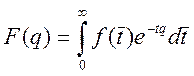 (1)

Установим связь между уравнением (1) и формулой преобразования Лапласа:

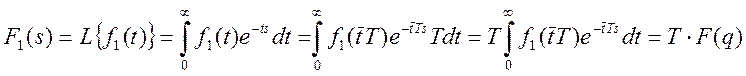
Здесь

Таким образом имеем:

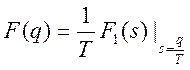  (2)

Оригинал определяется по формуле обращения:

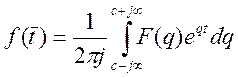  (3)

Где C – абсцисса абсолютной сходимости.  для функции .

Было показано, что значение оригинала, получаемое по формуле (3) в точках разрыва  определяется по формуле:

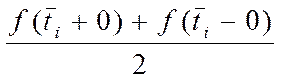
Подставим в соответствие функции  множество смещенных функций , значение которых в точках непрерывности функции  совпадает со значением этой функции, когда . Таким образом, смещенную решетчатую функцию можно определить следующим образом:

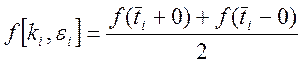
Функция  является оригиналом, если является оригиналом функция . В этом случае выполняется условие , где .

Теперь положим, что , тогда получим:

 при

Таким образом смещенная решетчатая функция также является оригиналом. Введем следующее обозначение:

Тогда справедливы следующие формулы:

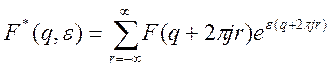  (4)

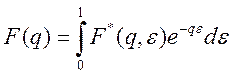    (5)

Таким образом - преобразование позволяет определить функцию для соответствующей решетчатой функции  по заданному изображению максимума функции .