Синтез линейных импульсных систем модальным методом

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА УПРАВЛЕНИЯ И ИНФОРМАТИКИ В ТЕХНИЧЕСКИХ СИСТЕМАХ

ЛАБОРАТОРНАЯ РАБОТА №3

по дисциплине

Теория автоматического управления

СИНТЕЗ ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ МОДАЛЬНЫМ МЕТОДОМ

Выполнил ст. гр. УИТ-41

Печавин А. В.

Проверил преподаватель

Мартынова И. В. _______

«___» ___________2005

2005

Цель работы: Исследовать возможности модального метода синтеза цифровых регуляторов для линейных импульсных систем.

Исходные данные:

Исходная передаточная функция:

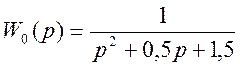
Шаг дискретизации T=0.2

Желаемые корни: λ₁=0,05; λ₂=0,2; λ₃=0

1.  Выполнение расчета дискретной передаточной функции по заданной непрерывной функции

Найдем дискретную передаточную функцию используя матричный метод.

          По заданной передаточной функции запишем дифференциальное уравнение:

y” + 0,5y’ + 1,5y = u

            Перейдем к уравнениям в пространстве состояний

y = x₁

y’ = x’₁ = x₂                       x’₂ + 0,5x₂ + 1,5x₁ = u

y” = x’₂

     x’₁ = x₂

     x’₂ = -1,5x₁ – 0,5х₂ + u

     y = x₁

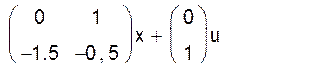
=>   X’ =

        Y = (1 0)x

            Следовательно, матрицы:

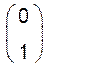
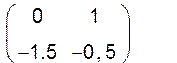
    =                            ;     =                    ;       = (1  0)

            По формуле (4) определим матрицы А и В

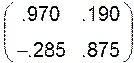
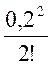
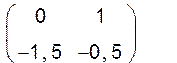
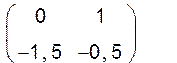
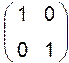
             +                         0,2 +                       ²·          =

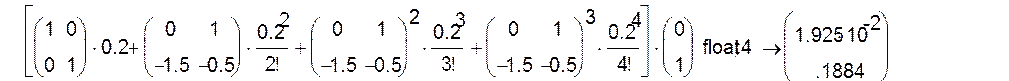
            Матрицы С и     совпадают.

          Разностные уравнения имеют вид:

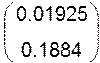
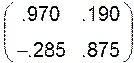
      X’(k+1) =                          x(k) +                    u(k)

      Y(k) = (1  0)x(k)

            Дискретную передаточную функцию с фиксатором нулевого порядка находим по формуле:

W(z) = C{ZI-A}^-1B

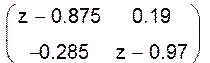
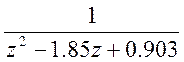
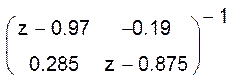
{zI – A}^-1 =                                     =                            

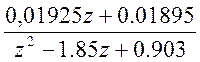
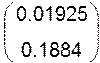
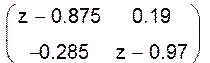
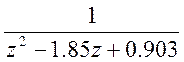
W(z) =   (1  0)                                                                                      =

2.  Для объекта, математическая модель которого задана передаточной функцией:

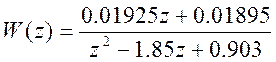
выполнить синтез астатического регулятора модальным методом по формулам:

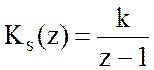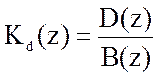, , где D(z)=d₁z + d₀. Желаемые корни соответствуют минимальной длительности процессов в замкнутой системе.

Характеристическое уравнение замкнутой синтезированной импульсной системы имеет вид: С(z) = (z-λ₁)(z-λ₂)(z-λ₃) = z³ - 0,25z² + 0,01z

Кроме того: (z-1)[z² - 1.85z + 0.903 + d₁z + d₀] + k(0.01925z + 0.01895) = 0

Получим систему:

      d₁ – 2.85 = 0

     d₀ + 2.753 + 0.01925k – d₁ = 0

      -0.903 – d₀ + 0.01895k = 0

Решая систему, получим значения коэффициентов:

d₁ = 2.85; d₀ = -0.407; k = 26.178.

Т.о. выражения корректора статики и динамики:

 ;

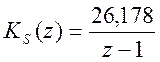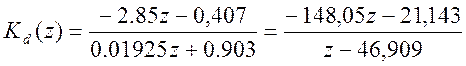
3.  На рисунке 1 изображена замкнутая дискретная система без регулятора и с регулятором. Переходные процессы обоих систем представлены на рисунке 2.

Переходный процесс с регулятором на звеньях задержки совпадает с моделью регулятора в общем виде, что подтверждает правильность построения модели на звеньях задержки.

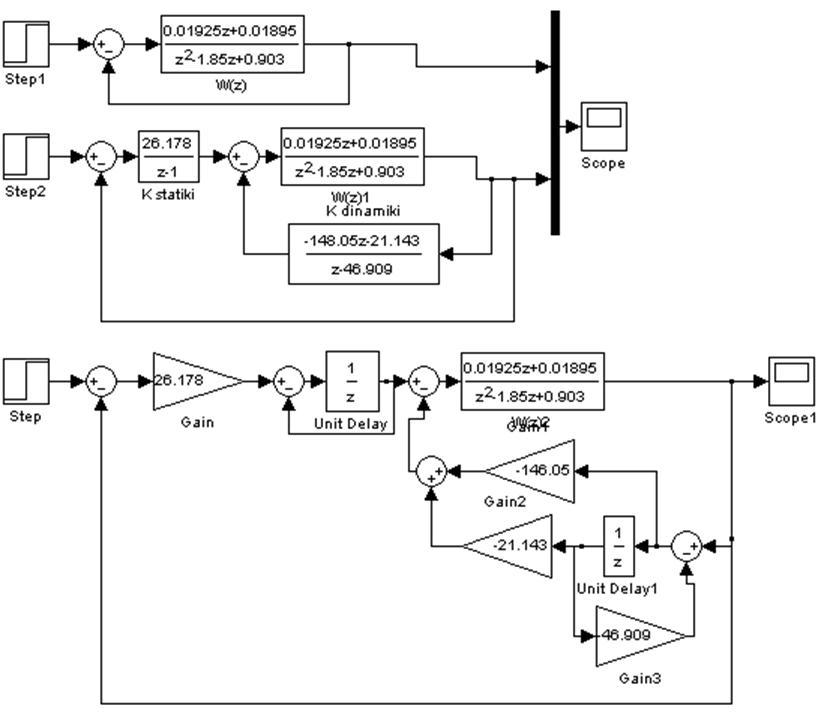
Рисунок 1 – Модели дискретных систем без регулятора и с регулятором,

и дискретной системы в звеньях задержки

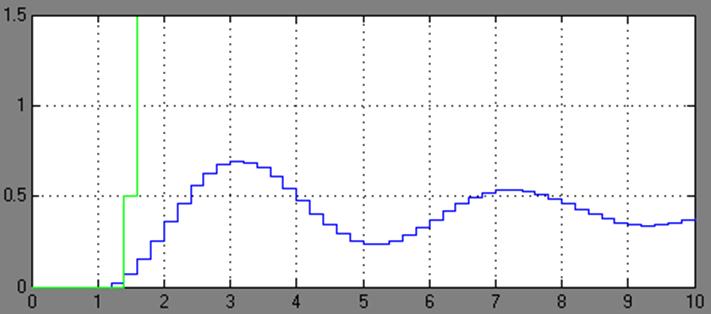
Рисунок 3 – Модель дискретной системы в звеньях задержки

Вывод: Рассмотрев все характеристики звеньев (с регулятором и без него), можно говорить о резком ухудшении характеристик системы, ввиду того, что переходный процесс системы с регулятором носит явно неустойчивый характер. Такое поведение может говорить о неправильности коэффициентов корректоров или невозможности подбора оных. Кроме того, время реакция системы увеличилось, что является также негативным фактором. Таким образом, в ходе выполнения лабораторной работы была получен регулятор с неудовлетворительными характеристиками.