
Схема электрической цепи и ее параметры
R2 = R3 = 50 Ом; C = 140 мкФ; L = 125мГн; E = 100В
Классическим методом найдем i1(t) и i2(t) после поочередного включения рубильников.
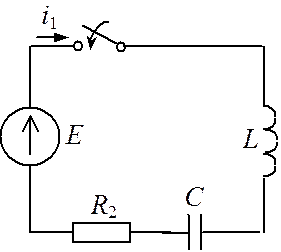
Рис. 1.
1) Запишем дифференциальное уравнение по схеме (рис. 1) и найдем принужденную составляющую в установившемся режиме:
uC+uL+ i1R2=E
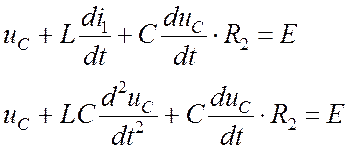
Следовательно uCпр = E = 100В.
2) Найдем корни характеристического уравнения и определим вид свободной составляющей uCсв:
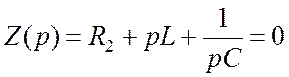
![]()
![]()
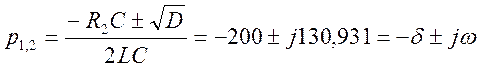 ,
,
следовательно, в цепи происходят затухающие колебания и
uCсв![]()
![]() =
=![]()
3) Определяем uC(t) и i1(t)
uC(t)=uCпр+uCсв=E+![]()
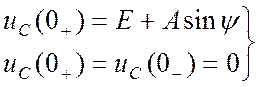 =>
=> ![]()
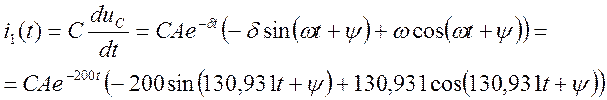
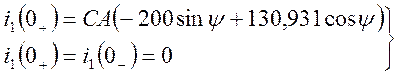 =>
=>![]()
Коэффициенты ![]() и
и ![]() определим из системы уравнений:
определим из системы уравнений:
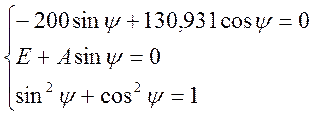
Решая систему в MathCad 14 получим:
![]()
А=-182.574
В итоге: ![]()
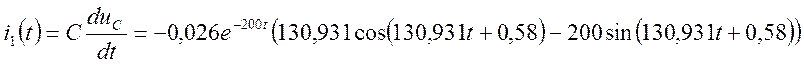
![]()
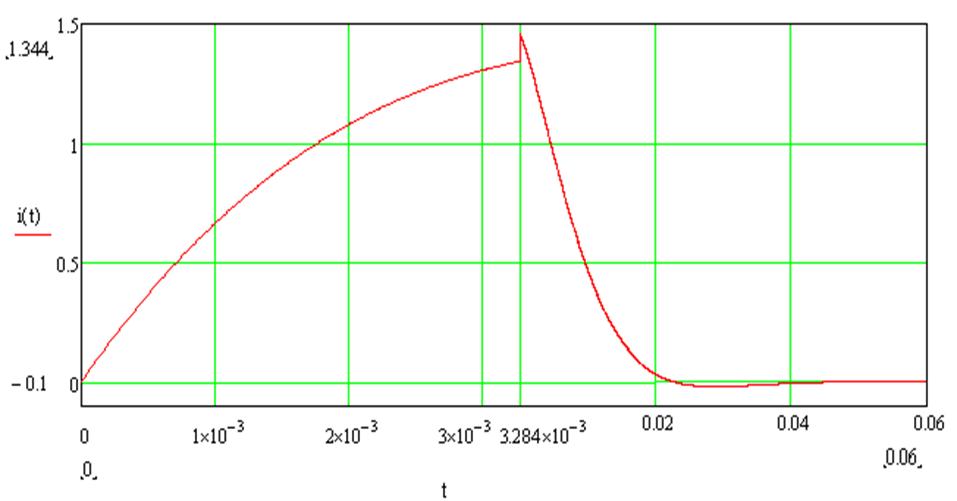
4) Найдем время замыкания второго ключа, а также ток через катушку и напряжение на конденсаторе в этот момент:
![]() 3.284*10-3
с
3.284*10-3
с
![]() =1,321 А
=1,321 А
![]() 19,868 В
19,868 В

Рис. 2.
1) Определим независимые начальные условия:
![]() 1,321 А
1,321 А
![]() 19,868 В
19,868 В
2) Определим зависимые начальные условия, пользуясь системой уравнений, составленной по законам Кирхгофа по схеме (рис. 2):
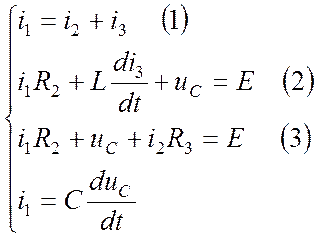
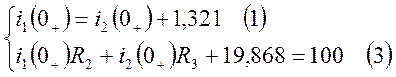
Подставим (1) в (3):
![]()
В итоге:
![]() А;
А; ![]() А
А
Из (2) находим:
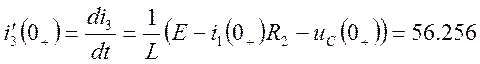 А/с
А/с
Продифференцируем исходную систему:
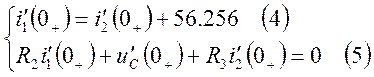
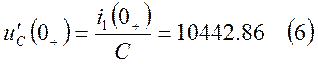
Подставим (6) в (5):
![]()
Подставим (4) в (7):
![]()
В итоге:
![]() А/с;
А/с; ![]() А/с
А/с
3) Найдем корни характеристического уравнения
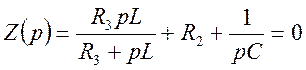
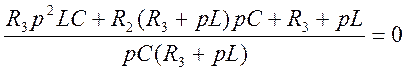
![]()
![]() =0
=0
![]() , следовательно,
в цепи происходят затухающие колебания.
, следовательно,
в цепи происходят затухающие колебания.
4) Находим принужденную составляющую тока i1пр и i2пр. В установившемся режиме ток через конденсатор равен нулю, поэтому i1пр = i2пр = 0.
5) Определим i1(t)
Свободную составляющую тока i!св запишем в виде
i1св
![]()
![]() =
=![]()
i1(t) = i1пр + i1св = 0 + ![]()
![]()
Коэффициенты ![]() и
и ![]() определим из системы уравнений,
записанной при
определим из системы уравнений,
записанной при ![]() :
:
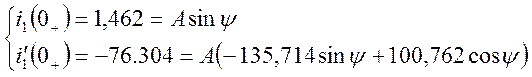
![]()
![]()
В итоге, переходный ток ![]()
6) Определим i2(t)
Свободную составляющую тока i2св запишем в виде
i2св
![]()
![]() =
=![]()
i2(t) = i2пр + i2св = 0 + ![]()
![]()
Коэффициенты ![]() и
и ![]() определим из системы уравнений,
записанной при
определим из системы уравнений,
записанной при ![]() :
:
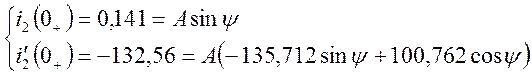
![]()
![]()
В итоге, переходный ток ![]()
1) Начертим операторную схему замещения (рис. 9)
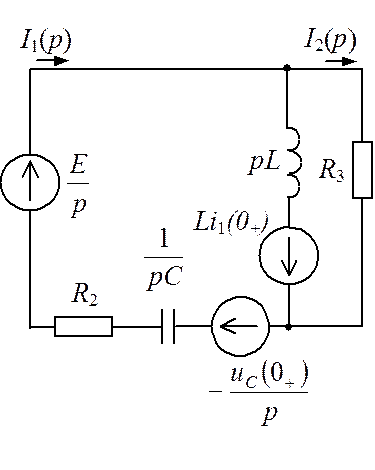
Рис. 3.
2) Составим уравнения по законам Кирхгофа для схемы (рис. 3) и определим изображение тока I2(p):
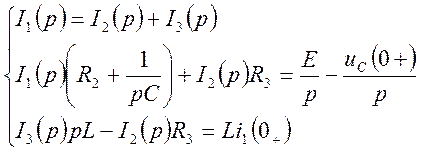
|
|
|
|
|
|
|
|
|
|
|
|
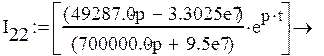
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.