Кафедра: УИТ
Специальность: УИТ
Факультет: вечерне-заочный
Теоретические основы электротехники
Выполнил студент гр. УИТ-31в
Бухарев Сергей Владимирович
Проверилпреподаватель
Зайцев Александр Васильевич
|
Задача №1.
Произвести синтез электрической цепи по известному операторному выражению, составить выражение входной проводимости Y(p), реализовать на схеме.
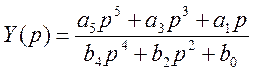 ;
;
a5 = 20; a3 = 21; a1 = 4; b4 = 20; b2 = 17; b0 = 1.
Составляем выражение входной проводимости:
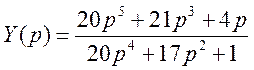 .
.
По лестничной дроби восстанавливаем электрическую схему и значение параметров:
|
p p |
2p2+1 2p2 |
4p3+3p 4p3+2p |
20p4+17p2+1 20p4+15p2 |
20p5+21p3+4p 20p5+17p3+p |
20p4+17p2+1 |
|
|
p |
||||||
|
4p3+3p |
||||||
|
5p |
||||||
|
2p2+1 |
||||||
|
2p |
||||||
|
p |
||||||
|
2p |
||||||
|
1 |
||||||
|
p |
||||||
|
0 |
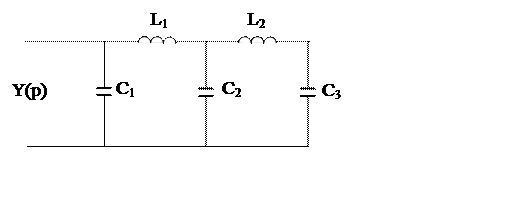
C1 = 1 Ф; С2 = 2 Ф; С3 = 1 Ф; L1 = 5 Гн; L2 = 2 Гн.
Задача №2.
1. Провести z – преобразование входной последовательности.
2. Перейти от передаточной функции аналогового четырехполюсника соответствующего цифрового W(z).
3. Реализовать передаточную функцию цифрового четырехполюсника в виде схемы.
4. Найти z – преобразование выходной последовательности Y(z) = W(z)∙X(z).
5. Записать выражение для выходной последовательности y(nT).
Входная последовательность x(n) = 0.9n ∙ U(n);
Дискретное время Тδ = 0,05 с;
Передаточная функция
аналогового четырехполюсника 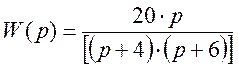
Решение:
1) Находим z - преобразование входной последовательности используя таблицу z – преобразования.
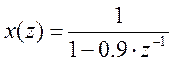
2) Перейдём от передаточной функции аналогового четырехполюсника к передаточной функции цифрового четырехполюсника используя обратную разность.
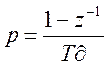 ;
;
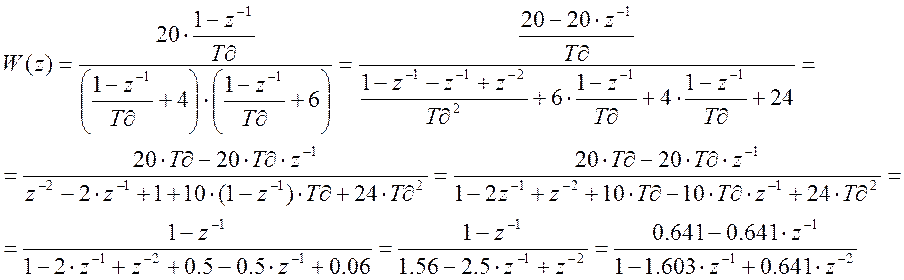
 3) По данной передаточной
функции строится цифровая схема.
3) По данной передаточной
функции строится цифровая схема.
4) Находим выходную последовательность.
y(z) = x(z) ∙ w(z);
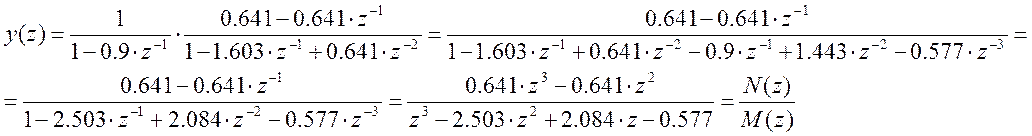
M(z) = (1 – 0.9∙z-1)∙(1 – 1.603∙z-1 + 0.641∙z-2);
M(z) = 0;
1 – 0.9∙z-1 = 0; 1 – 1.603∙z-1 + 0.641∙z-2 = 0;
z0 = 0.9; z2 – 1.603∙z + 0.641 =0;
D = b2 – 4∙a∙c = 2.57 - 2.56 = 0.01;
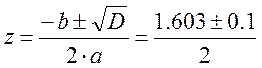 ;
;
z1 = 0.8515; z2 = 0.7515.
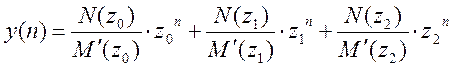
N(z) = 0.641∙z3 – 0.641∙z2; N(z0) = -0.052; N(z1) = -0.069; N(z2) = - 0.09.
M(z) = z3 -2.503∙z2 + 2.084∙z – 0577; M’(z) = 3∙z2 – 5.006∙z + 2.084;
M’(z0) = 0.0086; M’(z1) = - 0.0035; M’(z2) = 0.016;
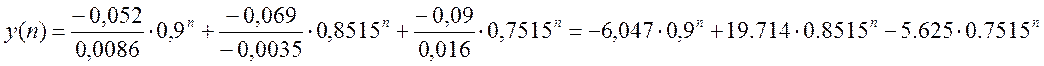
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.