|
|
Т, с |
L, мГн |
С, мкФ |
R1, Ом |
|
70 |
0,025 |
69,28 |
292,8 |
17,32 |
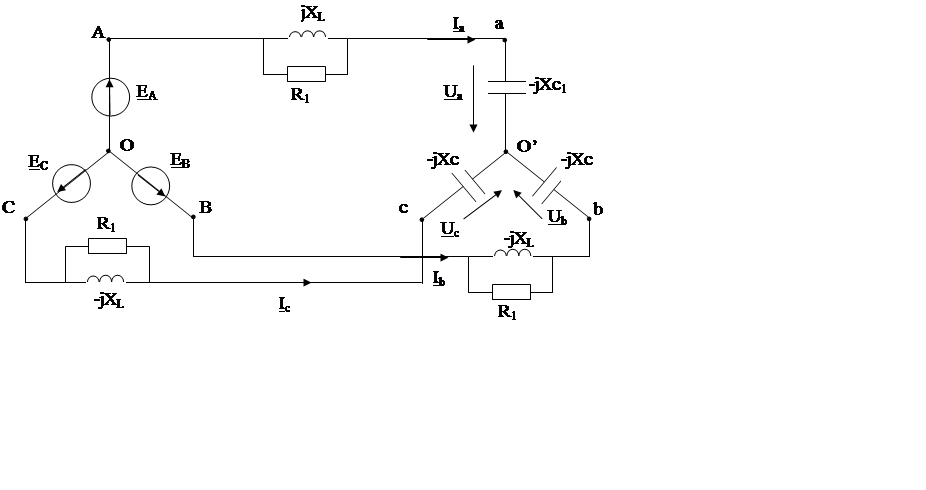
На рис.1 приведена схема трёхфазной цепи. В каждой из них имеется трёхфазный генератор (создающий трёхфазную симметричную синусоидальную систему э.д.с.) и симметричная нагрузка. Значения амплитуды э.д.с. фазы генератора ЕАm , периода Т, параметров R1, L,C приведены в таблице значений. Начальную фазу э.д.с. eA принять нулевой. Требуется: определить мгновенное значение напряжения между точками с и а, а также подсчитать активную мощность трёх фазной системы.
 |
Найдем индуктивное и емкостное сопротивления по формулам:
![]()
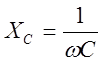 ,
,
где 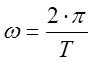 - круговая частота.
- круговая частота.
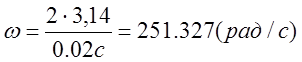 ;
;
![]()
![]()
Исходя из рис.1 определим фазное и линейное сопротивления:
![]() ;
;
![]()
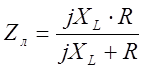
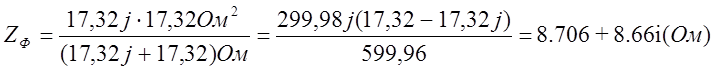
По найденным значениям рассчитаем ток
![]() , а исходя из его результата, найдем
все остальные токи.
, а исходя из его результата, найдем
все остальные токи.
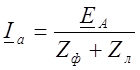 ;
;
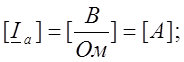
Ia = 6,089 + 3.447j
![]()
Ib = -0.059 – 6.997j
Рисунок2 0‑1
![]()
Ic = -6.03 + 3.549j
Определим фазные напряжения приемника:
![]()
![]()
Ua = 46.846 - 82.74j = 95e-60,5j
![]()
Ub = 46.846 - 82.74j = 95 e179,5j
![]()
Uc = 48.231 + 81.94j = 95e55,5j
Найдем ЭДС генератора:
![]()
![]()
![]()

По выше найденным значениям построим векторную диаграмму:
Масштабы: mU= В/см
mI= А/см
Для того, чтобы найти мгновенное значение напряжения между точками с и а , сначала надо найти Uса по второму закону Кирхгофа:
- Ib*Zл+UAb=
-EB + EA ![]() UAb=-EB
+ EA + Ib*Zл;
UAb=-EB
+ EA + Ib*Zл;
UAb= 2.51*103+4.182*10 3j(B).
Перейдем к мгновенным значениям по формуле:
UAb = UAbmsin(wt+a)
UAbm = UAbÖ2
UAb = Ö(141,9242 + 83,5392)ej(arctg(83,539/-141,924)+180) = 83,539e149,5j
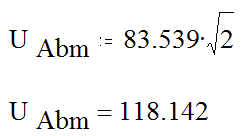
В итоге получим, что:
uAb = 83,539sin(wt + 149,5)
Определим активную мощность трехфазной схемы (рис.1) по следующей формуле:
![]()
где Ia* = 6,089 + 3.447j (А);
![]()
![]()
|
L, мГн |
С, мкФ |
Т, с |
Um ,B |
Rн ,Ом |
|
5,1 |
2,08 |
1,1*10-3 |
97 |
38,6 |
Рассматривая схему, приведённую на рис.2, как схему фильтра, работающего на согласованную нагрузку:
а) определить значения граничных частот полосы прозрачности фильтра ( частот среза);
б) Качественно построить зависимость характеристического сопротивления Z0, затухания а и сдвига по фазе b в функции частоты w;
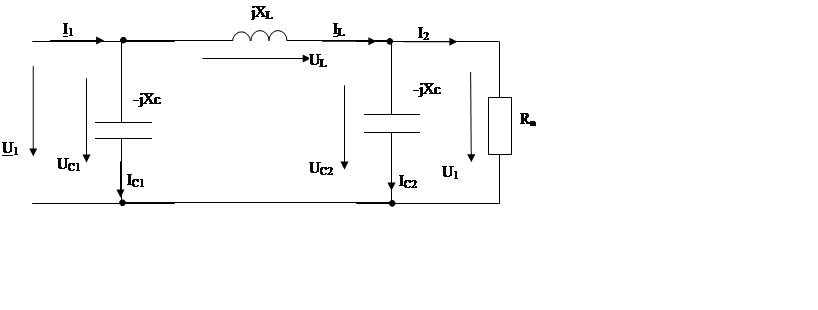 в) На вход низкочастотного фильтра подать напряжение U1=U1msinwt, На вход высокочастотного фильтра
подать напряжение U1=U1msin3wt. Для указанного напряжения
определить численные значения постоянной передачи g=а+jb, характеристического сопротивления Zc, напряжений и токов во всех ветвях
схемы и построить по ним векторную диаграмму токов и напряжений фильтра.
в) На вход низкочастотного фильтра подать напряжение U1=U1msinwt, На вход высокочастотного фильтра
подать напряжение U1=U1msin3wt. Для указанного напряжения
определить численные значения постоянной передачи g=а+jb, характеристического сопротивления Zc, напряжений и токов во всех ветвях
схемы и построить по ним векторную диаграмму токов и напряжений фильтра.
![]()
![]()
![]()
![]() L
L
U1(t) C C U2(t)
 |
Рис.2
Решение
![]()
![]() а)
а)
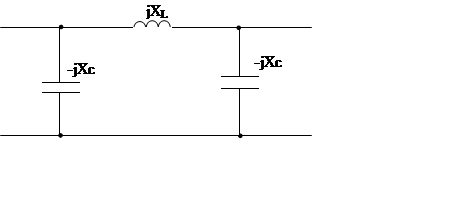 |
Данный нам фильтр является низкочастотным (П-схема). Следовательно значение граничной частоты полосы прозрачности фильтра будет определятся формулой:
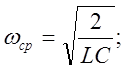
Найдем это значение.
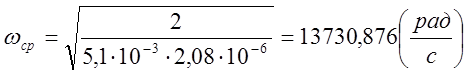
б) Найдем характеристическое сопротивление Zо по формуле:
![]() ,
,
где Z1K и Z1X определяются из опытов короткого замыкания и холостого хода.
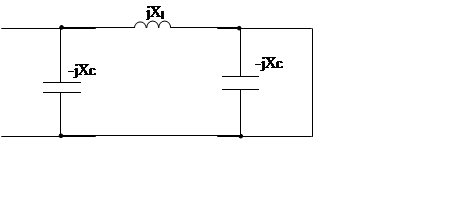
По рис.4 определим Z1K .
 |
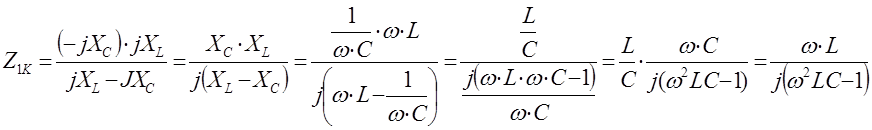 .
.
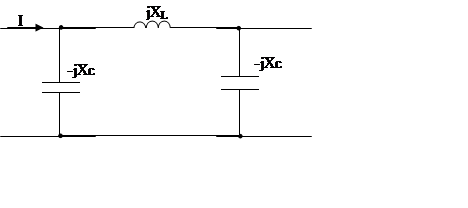
Теперь по рис.5 определим Z1Х
 |
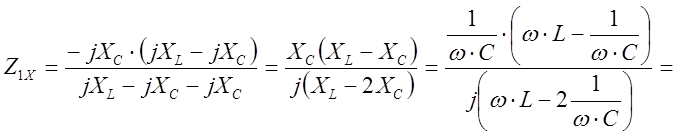
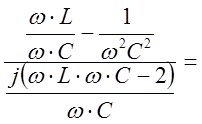
![]()
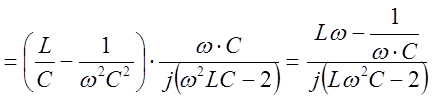 .
.
Тогда Z0 ,будет равно
![]()
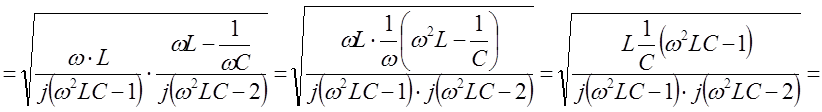
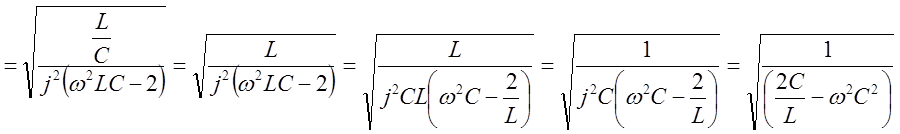 .
.
![]()
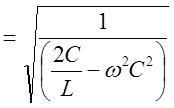 .
.
Исходя
из полученной формулы для ![]() , имеем:
, имеем:
при w=0, Z0=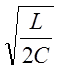 .
.
при w=![]() ,
Z0=0
,
Z0=0
Качественно
построим зависимость характеристического сопротивления ![]() , затухания а и сдвига по фазе
в функции частоты
, затухания а и сдвига по фазе
в функции частоты ![]() .
.
в) Определим численное значение постоянной передачи g по формуле:
g=a+jb,
где a=0 , а b=arccosa11.
Коофициент а11 низкочастотных фильтров определяется следующим образом:
a11=1-wр2LC ,
где wр=![]() - рабочая частота низкочастотного
фильтра;
- рабочая частота низкочастотного
фильтра;
wр 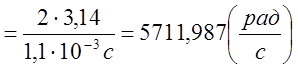 .
.
![]()
Тогда:
b=arccos(0,654)»49,1640
Рассчитаем Z0
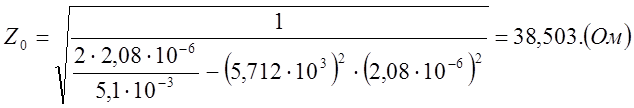
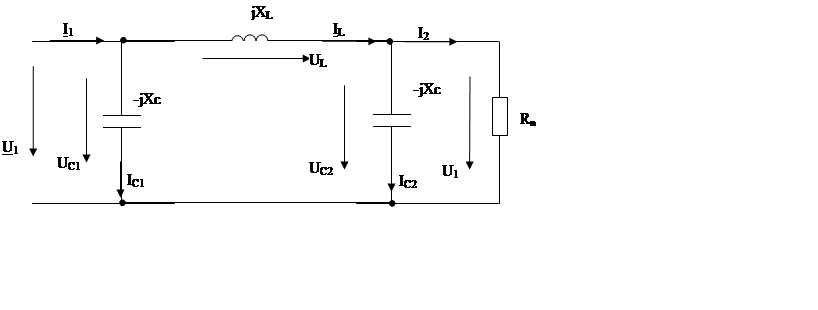 |
Рис.6
XL=wрL; XC=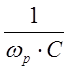 ;
;
XL=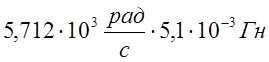 =29,131 (Ом);
=29,131 (Ом);
XC=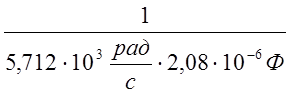 =84,168 (Ом).
=84,168 (Ом).
U1 = Umej0 = Um= 97 (B);
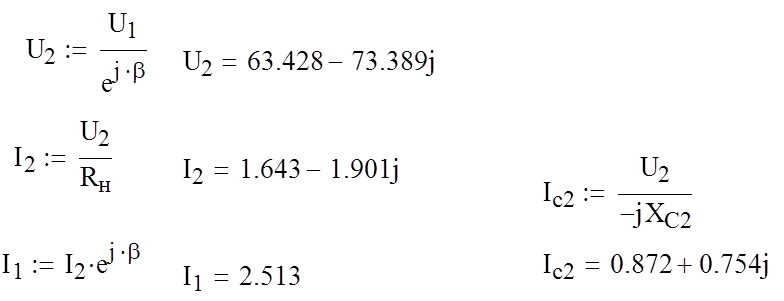
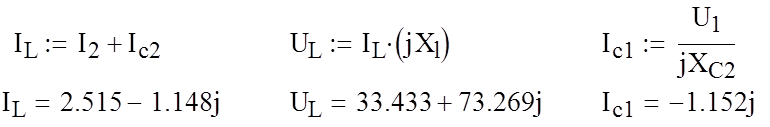
![]() Получили:
Получили:
U1 = 97 (B);
U2 = 63.428 – 73.389j (B);
UL = 33,433 + 73,269j(B).
![]() I1 = 2,513 (A);
I1 = 2,513 (A);
I2 = 1,643 - 1,901j (A);
IC2 = 0,872 + 0,754j (A);
IC1 = - 1,152j (A);
IL = 2,515 - 1,481j (A).
По найденным значениям построим векторную диаграмму.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.