Вариант 23
|
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
E1 |
E2 |
E3 |
Ik1 |
Ik2 |
Ik3 |
|
Ом |
В |
А |
|||||||||
|
16 |
20 |
12 |
30 |
42 |
52 |
50 |
- |
34 |
0 |
- |
0,5 |
Схема №1
c
![]()
![]()
![]()
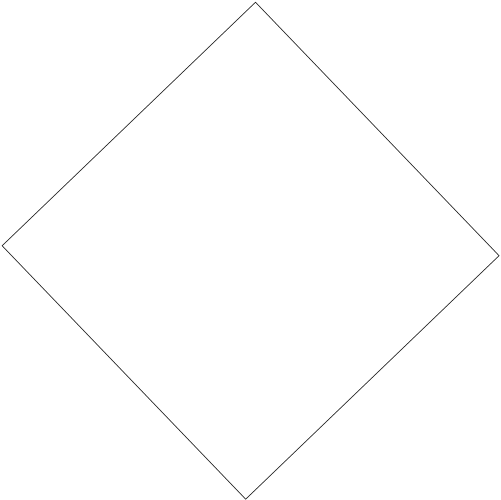

 R5
R5
R4
 Jk1
Jk1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]() b E1
b E1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ik3
R3 d
d
Ik3
R3 d
d
![]() m R1
m R1
![]()
![]() n I1
n I1

![]()
 R6 R2
R6 R2
![]()
 E3
E3
![]()
![]() a
a
![]()
![]()
![]()
 Изменим схему 1,
заменяя в ней источники тока на ЭДС, учтя что E3/=Jk3*R3,
Е\1=Jк1*R1= 0, т.е. Jk1=0
;
Изменим схему 1,
заменяя в ней источники тока на ЭДС, учтя что E3/=Jk3*R3,
Е\1=Jк1*R1= 0, т.е. Jk1=0
;
Схема №2.
I3 c
![]()
![]()
![]()
![]()
![]() I5
I5


![]()


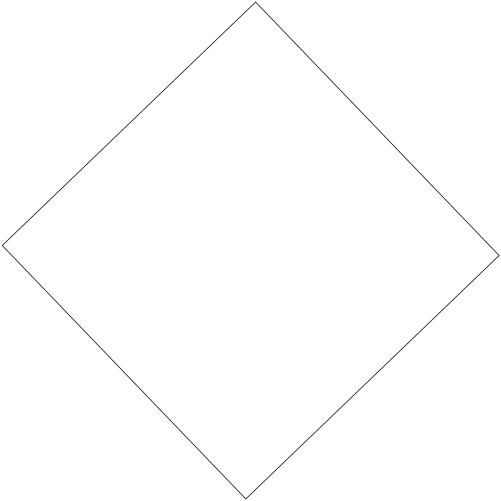 E\3
E\3
R5 R4
![]() I I4
I I4
![]() 3
3

![]() R1 1 E1
R1 1 E1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() R3
III
b
d
R3
III
b
d
 I1
I1

![]() 2
II
2
II

 R2
R2
![]()
![]() E3
E3
![]() R6 I2
R6 I2
I6
![]()
![]() a
a
Произведем анализ схемы 2.
Число узлов n=4; Число ветвей m=6.
I. Непосредственное применение законов Кирхгофа.
Расставим произвольно направления токов в ветвях. Составим по I закону Кирхгофа (n-1)=3 уравнение.
Для узла c: I3 + I5 - I4= 0; Для узла b: I1-I5+I6=0; Для узла d: -I1-I2+I4=0.
Составим по 2 закону Кирхгофа (m-mj)-(n-1)=6-3=3 уравнения для схемы 2. Для этого произвольно выберем направление обхода в каждом контуре.
1 контур: I1R1+I5R5+I4R4=E1 ;
2 контур: -I1R1+I2R2+I6R6=-E1;
3 контур: I3R3-I5R5-I6R6=E3+E\3;
Получим систему уравнений c шестью неизвестными:
![]() I1R1+I5R5+I4R4=Е1;
I1R1+I5R5+I4R4=Е1;
-I1R1+I2R2+I6R6=-E1;
I3R3-I5R5-I6R6=E3+ Е\3; (1)
I3+I5-I4=0;
I1-I5+I6=0;
-I1-I2+I4=0.
II. Метод контурных токов (МКТ)
![]() I1=I11-I22;
I1=I11-I22;
I2=I22;
I3=I33; (2)
I4=I11 ;
I5=I11 – I33 ;
I6=I22-I33;
Решаем систему относительно контурных токов
![]() I11(R1+ R4+ R5)-I22R1-I33R5=E1;
I11(R1+ R4+ R5)-I22R1-I33R5=E1;
-I11R1 +I22(R1+ R2+ R6)-I33R6=-E1;
-I11R5 –I22 R6 + I33(R3+ R5+R6)=E3 + Е\3.
Подставляя в получившуюся систему все численные значения известных величин, решаем её методом Крамера-Копелли
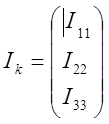 - матрица неизвестных
токов;
- матрица неизвестных
токов; 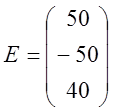 - матрица ЭДС.
- матрица ЭДС.
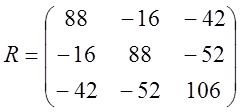 -матрица
коэффициентов при неизвестных;
-матрица
коэффициентов при неизвестных;
Найдём определитель матрицы R, ∆ :
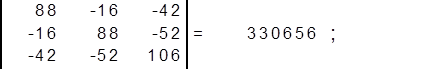
найдём определитель матрицы ∆1 :
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.