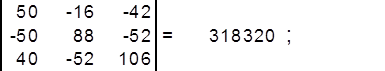
найдём определитель матрицы ∆2 :
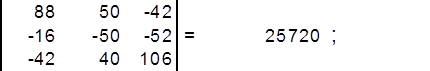
найдём определитель матрицы ∆3 :
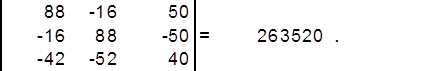
Тогда искомые контурные токи запишутся в матричной форме
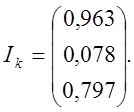
Подставляя полученные значения контурных токов в систему (2) получим значение токов действующих в цепи
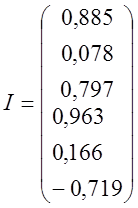 (4)
(4)
Матрица (4) и есть ответ задачи.
III. Метод узловых потенциалов (МУП).
Заземлим один узел d. Тогда φd=0. Найдем потенциалы оставшихся узлов а,b,c. Запишем токи, действующие в ветвях по закону Ома для активного участка цепи.

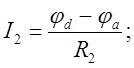
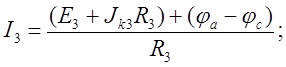
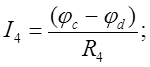
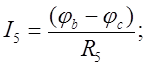
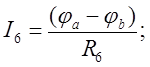 (5)
(5)
Получим систему из трёх уравнений
` ![]() φф(g2 +g3 +g6)-
g6φи- g3φс=-g3 (E3+E\3);
φф(g2 +g3 +g6)-
g6φи- g3φс=-g3 (E3+E\3);
-φфg6 + φи (g1 +g5 +g6)- g5φс=E1g1 ; (6)
-φф g3- φиg5+ φс (g3 +g4 +g5) = g3 (E3+E\3).
Решим полученную систему (6) относительно потенциалов в узлах используя метод Крамера-Коппели.
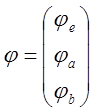 - столбцевая матрица
потенциалов узлов;
- столбцевая матрица
потенциалов узлов; 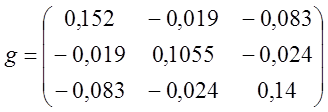 матрица проводимости
ветвей;
матрица проводимости
ветвей; 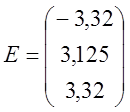 -матрица известных членов правой
части.
-матрица известных членов правой
части.
Высчитаем определитель матрицы проводимости g, ∆ :
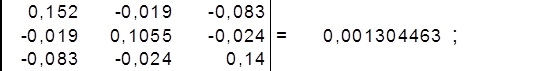
найдём определитель матрицы ∆1 :
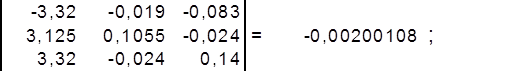
найдём определитель матрицы ∆2 :
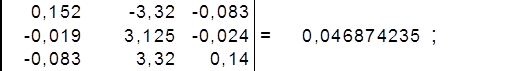
найдём определитель матрицы ∆3 :
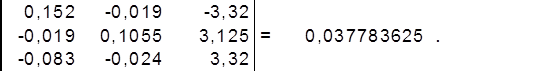
Отсюда получаем потенциалы узлов записанных в матричной
форме 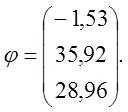
Подставляя в уравнения (5) соответствующие потенциалы узлов, получаем токи действующие в ветвях
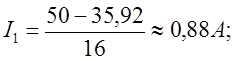
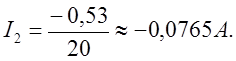
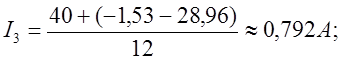
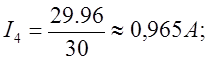
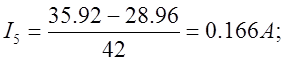
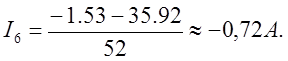
Получим столбцевую матрицу ответов 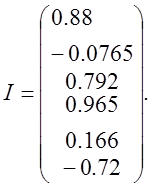
4. Результаты расчётов
Сравнительная таблица №1.
|
Метод |
Действительные токи в ветвях |
|||||
|
I1 |
I2 |
I3 |
I4 |
I5 |
I6 |
|
|
МКТ |
0,885 |
0,078 |
0,797 |
0,963 |
0,166 |
-0,719 |
|
МУП |
0,88 |
-0,0765 |
0,792 |
0,965 |
0,166 |
-0,72 |
|
Разница, ∆ |
0,005 |
0,0015 |
0,005 |
0,002 |
0 |
0.001 |
5. Баланс мощностей исходной схемы
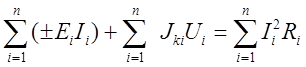
E3I3+ Jk3R3I3 + E1I1= I12R1+ I22R2+ I32R3+ I42R4+ I52R5+ I62R6 .
34*0,792+0,5*12*0,792+50*0,88=0,882*16+0,07652*20+0,7922*12+0,9652*30+0,1662*42+0.722*52
75,68=76
6. Расчёт тока методом эквивалентного генератора
Для расчёта тока I1 методом эквивалентного генератора необходимо теоретически найти два параметра: Uxx-напряжение холостого хода и rвн- внутреннее сопротивление эквивалентного генератора.
Разомкнём узлы b и d
Схема №3.
Ic
![]()
![]()
![]()
![]() c
c



 E\3
R5 R4
E\3
R5 R4


![]() Ib Контур № 4
Ib Контур № 4

![]() Uxx E1
Uxx E1
![]()
![]()
![]()
![]()
![]()
![]()
![]() R3
II
R3
II
I
![]()

![]()
 Ia
Ia

 E3
R2
E3
R2
R6
![]()
![]() a
a
В полученной схеме произвольно выберем направление токов в трёх ветвях и двух контурах. Выразим через контурные действующие токи. По второму закону Кирхгофа составим систему уравнений.
![]() Ia=I11;
Ia=I11;
Ic=I22; (7)
Ib=I11 – I22 .
По второму закону Кирхгофа составим систему уравнений.
![]() I11(R2+R4+ R5 +R6)-I22
(R5+ R6) =0;
I11(R2+R4+ R5 +R6)-I22
(R5+ R6) =0;
-I11 (R5+ R6 )+I22(R3+ R5+ R6)=E3+Jk3R3.
![]() Решим систему методом матриц.
Решим систему методом матриц.
![]()
![]()
|
|
|
-(R5+ R6) (R3+ R5+ R6) , E3+Jk3R3 40
Найдём определитель матрицы ∆R :
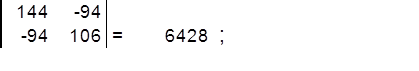
Найдём определитель матрицы ∆1 :

Найдём определитель матрицы ∆2 :
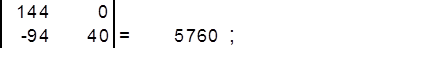
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.