Электротехника \ Теоретические основы электротехники

Расчёт электрической цепи

Страницы работы

9 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Содержание

1.1 Уравнения по законам Кирхгофа 3

1.2 Уравнения по методу контурных токов. Токи по ветвям 4

1.3 Метод узлового напряжения. Эквивалентная звезда 5

1.4 Определение тока в резисторе R6 методом эквивалентного генератора 6

1.5 Определение показание вольтметра. Баланс мощностей 8

1.6 Потенциальная диаграмма для внешнего контура 9

Список использованных источников 10

Дано:

Е1 = 10 В, Е2 = 32 В, Е3 = 10 В, R01 = 0.6 Ом, R03 = 1.0 Ом, R1 = 1.5 Ом, R2 = 6 Ом, R3 = 1 Ом, R4 = 7 Ом, R5 = 1 Ом, R6 = 5 Ом

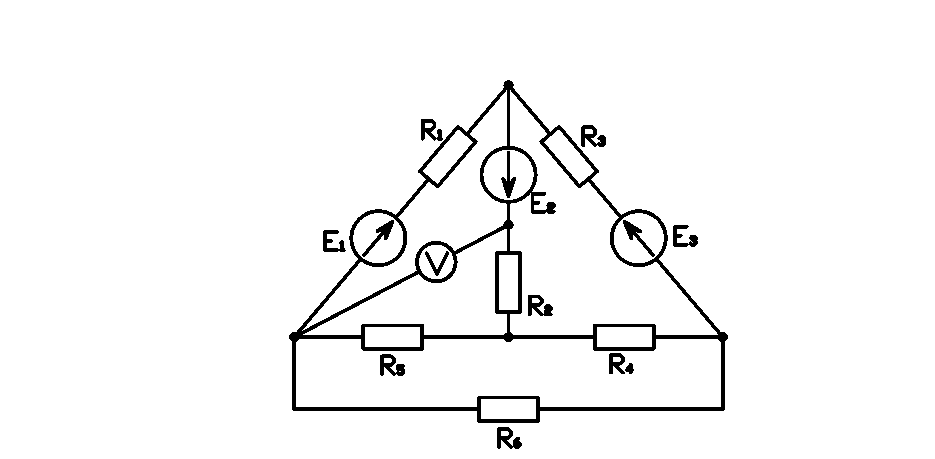
Решение:

1.1 Составим уравнения по законам Кирхгофа.

По первому закону

Обозначим узлы схемы буквами a, b, c, d, зададим направления токов.

По первому закону Кирхгофа:

для узла а - I1 + I5 – I6 = 0

для узла b I1 – I2 + I3 = 0

для узла c - I3 + I4 + I6 = 0

для узла d I2 – I4 + I5 = 0

По второму закону

для контура a b d а I1(R1 + R01) + I2 R2 + I5 R5 = Е1 + Е2

для контура b с d b -I2 R2 + I3(R3 + R03) – I4 R4 = -Е2 – Е3

для контура а с d а I4 R4 – I5 R5 – I6 R6 = 0

для контура a b с а I1(R1 + R01) - I3(R3 + R03) - I6 R6 = Е1 – Е3

1.2 Уравнения по методу контурных токов. Токи по ветвям

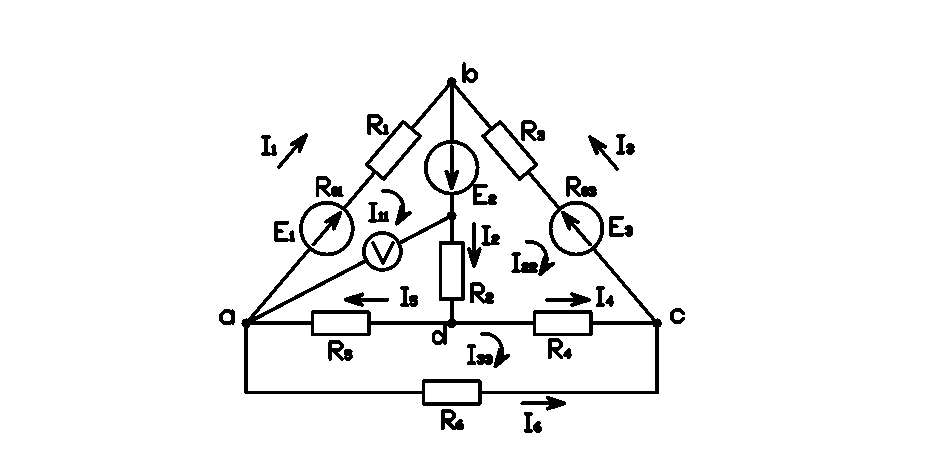
Составим систему уравнений

2.1I 11 + 6(I 11 - I 22) + (I 11 - I 33) = 42

-6(I 11 - I 22) – 2.0 - (I 22) - 7(I 33 - I 22) = -42

7(I 33 - I 22) – (I 11 - I 33) - 5(-I 33) = 0

9.1I11 - 6I22 - I33 = 42

-6I11 + 15I22 - 7I33 = -42

-I11 - 7I22 + 13I33 = 0

Матрица коэффициентов при неизвестных

9.1 -6 -1

А = -6 15 -7

-1 -7 13

Матрица свободных членов

В = -42

Матрица контурных токов Iк = А х В

3.364

Iк = -1.7813

-0.7004

Токи в резисторах

I1 = 3.364 А

I2 = 3.364 – (-1.7813) = 5.1452 А

I3 = 1.7813 А

I4 = -0.7004 – (-1.7813) = 1.0809 А

I5 = 3.364 – (-0.7004) = 4.0643 А

I6 = 0.7004 А

1.3 Метод узлового напряжения. Эквивалентная звезда.

Заменим треугольник резисторов R4, R5, R6 звездой ra, rc, rd

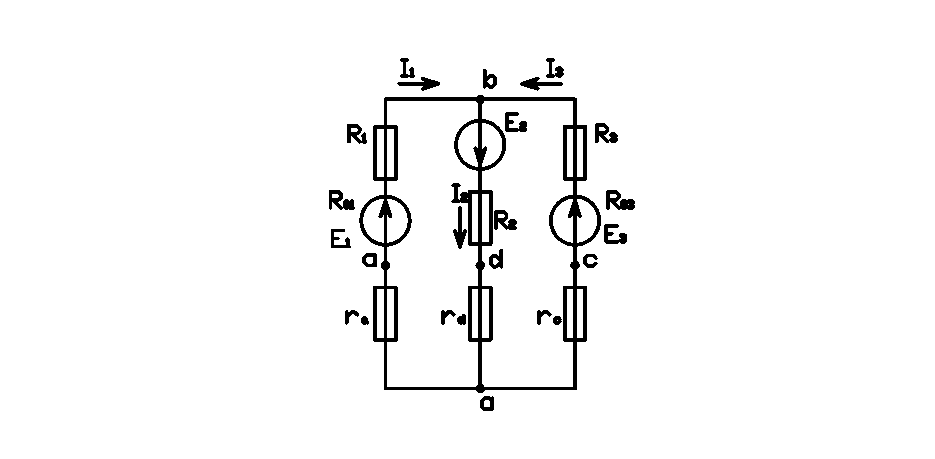
ra = R5 х R6 / R4 + R5 + R6 = 1 х 5 / 13 = 0.3846 Ом

ra = R4 х R6 / R4 + R5 + R6 = 35 / 13 = 2.6923 Ом

ra = R4 х R5 / R4 + R5 + R6 = 7 / 13 = 0.5385 Ом

Для определения потенциалов точек а, с, d рассмотрим первый закон Кирхгофа для узла b

I1 – I2 + I3 = 0

I1 = Е1 + (У0 – Уb) / R1 + R01 + ra = 10 + (У0 – Уb) / 2.4846

I2 = Е2 + (Уb – У0) / R2 + rd = 32 + (Уb – У0) / 6.5385

I3 = Е3 + (У0 – Уb) / R3 + R03 + rc = 10 + (У0 – Уb) / 4.6923

Подставив эти выражения токов и приняв У0 = 0, получим

Уb(1/ 2.4846 + 1/ 6.5385 - 1/ 4.6923) = -10/ 2.4846 + 32/6.5385 – 10/4.6923

-0.768535 Уb = -1.26185

Уb = 1.6419 В

I1 = 10 - 1.6419/ 2.4846 = 3.364 А

I1 = 32 + 1.6419/ 6.5358 = 5.1452 А

I1 = 10 - 1.6419/ 4.6923 = 1.7812 А

Потенциалы точек а, с, d

Уа = -I1 ra = -3.364 х 0.3846 = -1.29379 В

Ус = -I3 rс = -1.7812 х 2.6923 = -4.79552 В

Уd = I2 rd = 5.1452 х 0.5385 = 2.77069 В

Токи в резисторах

I4 = Уd – Ус / R4 = 2.77069 – (-4.79552) / 7 = 1.0809 А

I5 = Уd – Уа / R5 = 2.77069 – (-1.29379) / 1 = 4.0644 А

I6 = Уа – Ус / R6 = -1.29379 – (-4.79552) / 5 = 0.0703 А

Полученные значения токов в резисторах совпадают с аналогичными значениями, полученными методом контурных токов.

1.4 Определение тока в резисторе R6 методом эквивалентного генератора

Из исходной схемы исключаем резистор R6, оставшуюся схему считаем генератором, дающим напряжение U2 и имеющего внутреннее сопротивление rо.

U2 = Уа – Ус

Ток в резисторе R6 I6 = U2 / R6 + rо

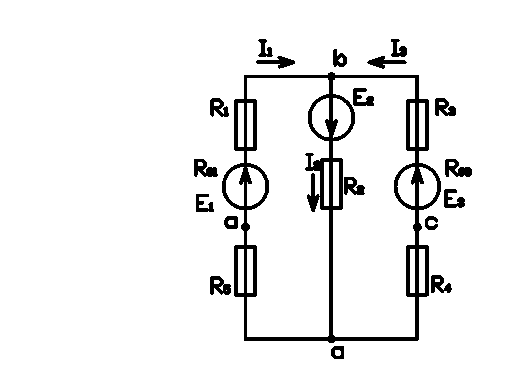
Находим Уа и Ус, используя первый закон Кирхгофа для узла b.

I1 – I2 + I3 = 0

I1 = Е1 + (Уd – Уb) / R1 + R01 + R5 = 10 + (Уd – Уb) / 3.1

I2 = Е2 + (Уb – Уd) / R2 = 32 + (Уb – Уd) / 6

I3 = Е3 + (Уd – Уb) / R3 + R03 + R4 = 10 + (Уd – Уb) / 9

Подставляя эти выражения токов и приняв Уd = 0, получим

– Уb(1 / 3.1 + 1 / 6 + 1 / 9) = -10 / 3.1 + 32 / 6 – 10 / 9

-0.600358 Уb = 0.996416

Уb = -1.6597 В

I1 = 10 + 1.6597 / 3.1 = 3.7612 А

I3 = 10 + 1.6597 / 9 = 1.29552 А

Потенциал Уа = - I1 х R5 = -3.7612 х 1 = -3.7612 В

Потенциал Ус = - I3 х R4 = -1.29552 х 7 = -9.06866 В

U2 = Уа – Ус = -3.7612 – (-9.06866) = 5.30746 В

Находим внутреннее сопротивление генератора rо.

Исключаем Е1, Е2, Е3

Внутреннее сопротивление генератора rо равно сопротивлению между точками а и с.

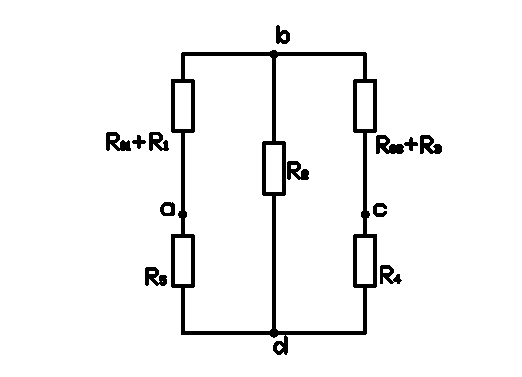
Треугольник резисторов (R1 + R01), R2, R5 заменяем звездой резисторов ra, rb, rd

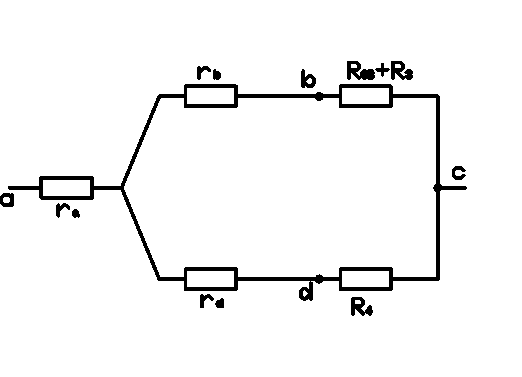
ra = (R1 + R01) х R5 / (R1 + R01) + R2 + R5 = 2.1 х 1 / 2.1 + 1 + 6 = 0.23077 Ом

rb = (R1 + R01) х R2 / (R1 + R01) + R2 + R5 = 2.1 х 6 / 2.1 + 1 + 6 = 1.38462 Ом

rd = R2 х R5 / (R1 + R01) + R2 + R5 = 6 х 1 / 2.1 + 1 + 6 = 0.65934 Ом

Внутреннее сопротивление генератора rо

rо = ra + [(rb + R3 + R03) х (rd + R4) / (rb + rd + R3 + R03 + R4)]

rо = 0.23077 + [(3.38462 х 7.65934) / (3.38462 + 7.65934)] = 2.57811 Ом

I6 = U2 / R6 + rо = 5.30746 / (5 + 2.57811) = 0.7004 А

Результат совпадает со значением I6, полученным методом контурных токов и узлового напряжения.

1.5 Определение показания вольтметра. Баланс мощностей.

Показание вольтметра определяем, применив второй закон Кирхгофа для контура, содержащего Е1, Е2, R1, R01, V.

I1(R1 + R01) + V = Е1 + Е2

V = Е1 + Е2 - I1(R1 + R01) = 42 – 3.364 х 2.1 = 34.9356 В

Баланс мощностей.

Мощность источников

Рu = I1 Е1 + I2 Е2 + I3 Е3 = 3.364 х 10 + 5.1452 х 32 + 1.7813 х 10 = 216.0994 Вт

Мощность потребителей

Рn = I1²(R1 + R01) + I2²R2 + I3²(R3 + R03) + I4²R4 + I5²R5 + I6²R6

Рn = 3.364² х 2.1 + 5.1442² х 6 + 1.7813² х 2 + 1.0809² х 7 + 4.0643² х 1 +

0.7004² х 5 = 215.9 Вт.

Мощность источников и мощность потребителей совпадает с точностью до 1 %, значит баланс выдержан.

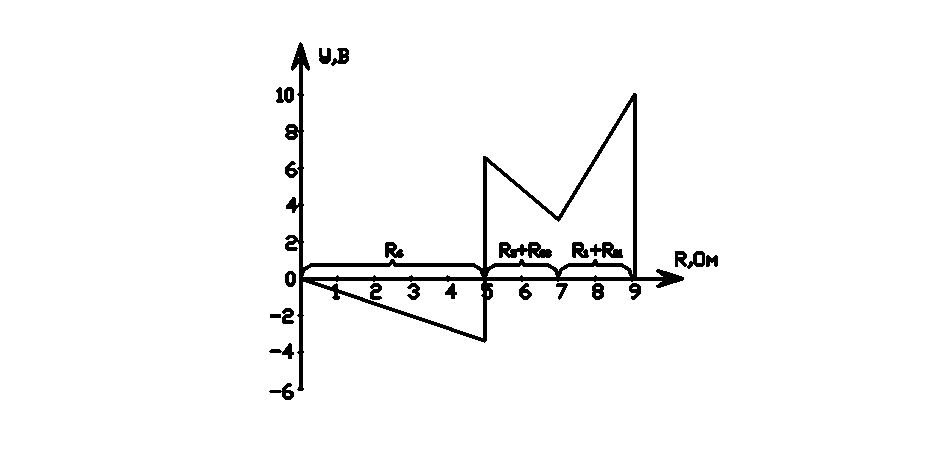
1.6 Потенциальная диаграмма

Внешний контур содержит Е1, Е3, R1, R01, R3, R03, R6. Будем обходить контур против часовой стрелки из узла а, потенциал которого примем Уа = 0. На участке а с потенциал изменяется на ∆Уb = I6R6 = 3.5 В. На участке с b потенциал сначала увеличивается на Е3 = 10 В, затем уменьшается на ∆У3 = I3(R3 + R03). На участке b а потенциал сначала увеличивается на ∆У1 = I1(R1 + R01), затем уменьшается на Е1 = 10 В.