Расчет системы с распределенными параметрами: распределение температуры по алюминиевой пластине

 ВВЕДИНИЕ

Моделирование – процесс замещения объекта исследования некоторой его моделью и проведение исследований на этой модели с целью получения необходимой информации об исследуемом объекте.

Различают два типа моделирования: предметное и абстрактное.

При первом способе моделирования строят физическую модель, соответствующим образом отражающую основные физический свойства и характеристики моделируемого объекта. При этом модель может иметь другую физическую природу, по сравнению с реальным объектом.

При абстрактном моделировании используют множество видов математических моделей, представляющие собой совокупность математических объектов и отношений между ними, адекватно отражающих физические свойства создаваемого технического объекта. В общем случае уравнение математической модели связывает физические величины, характеризующие состояние объекта.

Модель – физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие физические свойства и характеристики моделируемого объекта.

Процесс моделирования включает в себя несколько этапов:

а)  постановка задачи и определение свойств реального объекта, подлежащего исследованию;

б)  констатация затруднительности или невозможности реального объекта;

в)  выбор модели, хорошо описывающей основные свойства объекта, с одной стороны, и легко поддающаяся исследованию, с другой;

г)  исследование модели в соответствии с поставленной целью;

д)  проверка адекватности объекта и модели; если соответствий нет, то необходимо повторить п. а – г.

1 ИСХОДНЫЕ ДАННЫЕ

Рассчитать распределение тепла по алюминиевой пластине. Идентифицировать тип дифференциального уравнения. По заданному дифференциальному уравнению получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины. Построить статическую характеристику выходной величины, а также логарифмические характеристики.

Исходные данные:

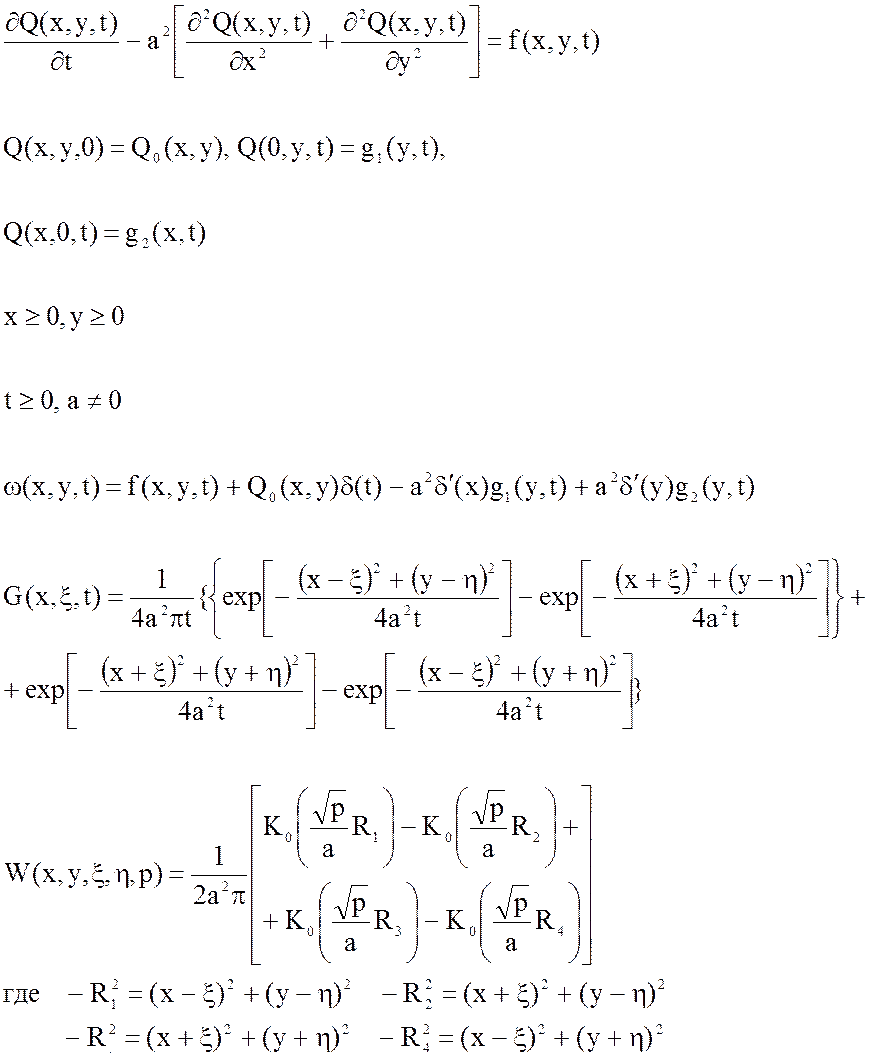
 2 ОСНОВНЫЕ ПОНЯТИЯ СРП

Первый этап в развитии ТАУ связан с управляемыми системами состояния, которые характеризуется поведением во времени t некоторого набора функций одной переменой t конечного числа n:

                                                                                  (1)

Подобные системы обычно описываются обыкновенными дифференциальными уравнениями или системами  дифференциальных уравнений относительно g(t) и называются системами с сосредоточенными параметрами. Модели большого числа объектов управления могут быть с достаточной для практической точности  точностью  ССП. По практике любой технический объект имеет вполне определенные геометрические размеры, поэтому функция характеризующая ее состояние изменяется в пределах пространственной области и следовательно зависит не только от времени, но и от пространственных координат.

Такие системы называются системы с распределенными параметрами. Состояние СРП описывается дифференциальным уравнением с частыми производными, интегральными уравнениями, а также гибридными. Функция состояния Q(x,t) определенная на пространственной области Д удовлетворяет уравнению:

                                     L[Q(x,t)]=f(x,t)   , t>0                                       (2)

  где  Д- открытая часть области Д не содержащая границы;

         L- некоторый заданный оператор(функция в частных производных);

         f(x,t)- известная функция характеризующая внешнее  воздействие на процесс.

   Если , то (2) – однородное уравнение,

              , то (2)- неоднородное уравнение.

   Если  g(x,t)- векторная функция состояния , то (2)-представляет собой систему уравнений.

Для получения единственного решения уравнения (2) необходимо дополнить начальными условиями, которые описываются некоторым линейным оператором

                                     N[Q(x,t)]=Q(x,t)   , t=0                                           (3)  

Полная система уравнений должна содержать граничные условия от Q(x,t)  которые характеризуют взаимодействие Q(x,t) с внешней средой должно выполнятся условие t>0 на границе области Д.

                                                                             (4)

   где  Г- линейный оператор;

          - внешние воздействие, которое можно рассматривать как второй вход объекта наряду с .

Если , то граничное условие однородное и наоборот.

Уравнения математической физики являются основой для построения математической модели элементов систем уравнений с распределенными параметрами. Для их практического применения основной сложностью является выбор уравнения, который могло бы с заданной точностью и степенью достоверности описать интересующий элемент системой управления.

Самостоятельно составлять и получать в частных производных является сложной  задачей, поэтому используют следующий алгоритм:

1) Выбирается система координат исходя из конструкции элемента СУ.

2)  Выбирается размерностьr пространственной области D  определения функции Q данной задачи.

3)  Наивысший порядок производных m функции Q по независимой временной производной t ограничивается двойной.

4)  Наивысший порядок производных n функции Q по пространственным переменным ограничивается двойной.

5)  Выбирается дифференциальное уравнение группы ( r, m, n)  в нужной системе координат.

6)  Уравнение «офизичивается», то есть производится конструирование размерностей. Это означает, что задается первичная размерность, либо входному возмущению f (x, y, z, t ), либо выходному сигналу Q (x, y, z, t ). В зависимости оттого, что интересует. Далее рассчитываются вторичные размерности исходя из конкретного вида уравнения и зависящая от первичных размерностей.

7)  Находится выходной сигнал и производится его сопоставление с ожидаемыми результатами.

8)  Если результат не устраивает, выбираем  другое уравнение и повторяем все процедуры заново.

Во многих случаях для описания физических процессов используют уравнений  с частыми производными до второго порядка включительно.

Так, например, процессы распространения тепловой энергии описывается уравнением теплопроводности

,

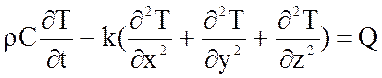где  и С – плотность и теплоемкость вещества,

       Т- температура,

       k- коэффициент теплопроводности,

        Q – плотность источника тепла.

Анализ стационарных состояний, например, статических тепловых, электрических, магнитных полях проводят,  используя уравнение Пуассона

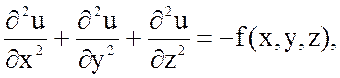
где u(x, y, z) – функция, описывающая статическое поле,

       f( x, y, z)- распределенные источники.

Несмотря на различие процессов,   все они могут быть представлены как частные случаи обобщенной формы дифференциального уравнения второго порядка.