Рассмотрим уравнение второго порядка с двумя независимыми переменными x и y:
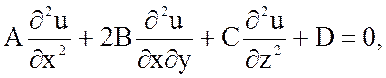 (1)
(1)
где A,B,C,D- некоторые функции, зависящие в общем случае от x, y,u.
На основании того, что уравнение 1 можно поставить в квадратичную форму
![]() по
природе различают следующие типы квазилинейных уравнений:
по
природе различают следующие типы квазилинейных уравнений:
1) гиперболический, если В2-4АС>0- его аналогом является волновое уравнение;
2) параболический, В2-4АС=0-его аналог уравнение теплопроводности;
3) эллиптический, если В2-4АС<0- аналог уравнение Пуассона или Лапласа.
3 ИДЕНТИФИКАЦИЯ ТИПА ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
ЗАДАНИЕ ВХОДНОГО И ВЫХОДНОГО ПАРАМЕТРОВ, НАЧАЛЬНЫХ И ГРАНИЧНЫХ УСЛОВИЙ
Так как данное дифференциальное уравнение содержит первую производную по времени, то оно относится к параболическому типу. Также это уравнение является неоднородным.
Выходным параметром Q(x,y,t) в данной системе является температура, распределяющаяся по пластине.
|
|
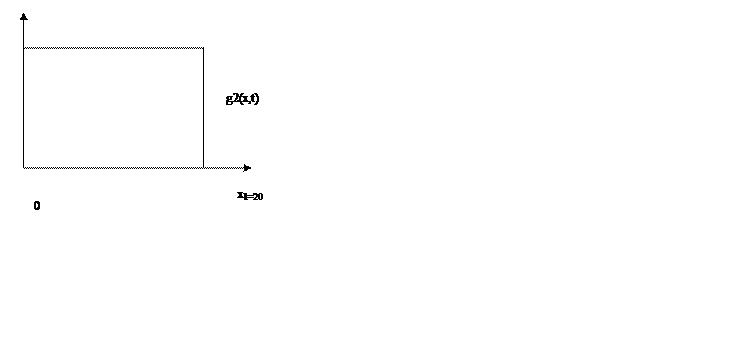
Рисунок 1-Геометрические размеры пластины.
Аналитическая форма представлена на рисунке 1, а графическая форма записи входного воздействия на рисунке 2.
![]()
|
|
Рисунок 2- Вид входного воздействия
Граничные условия представлены на рисунке 3.
g1 (y,t):=sin(0.5t)+20
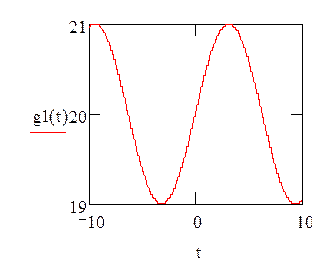
Рисунок 3- Граничные условия.
g2(x,t):=20
Зададим размерность входного возмущения.
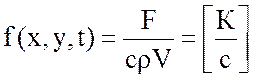 ,
,
где F- количество теплоты (теплой поток)
V-объем.
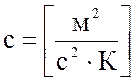 –
удельная теплоемкость алюминия.
–
удельная теплоемкость алюминия.
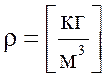 -
плотность алюминия.
-
плотность алюминия.
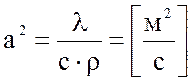 -коэффициент
температуропроводности,
-коэффициент
температуропроводности,
где ![]() -коэффициент
теплопроводности алюминия.
-коэффициент
теплопроводности алюминия.
Тогда а2 =0.884 м2/с.
Пусть x1 = 10-длина пластины, y1 = 20-ширина пластины.
Начальные условия:
![]() ,
что соответствует комнатной температуре пластины до начала действия
нагревательного элемента.
,
что соответствует комнатной температуре пластины до начала действия
нагревательного элемента.
Граничные условия:
![]() ,
что соответствует изменение температуры на x1 ребре пластины согласно рисунку 1.
,
что соответствует изменение температуры на x1 ребре пластины согласно рисунку 1.
![]() -
что соответствует изменение температуры на y1 ребре пластины согласно рисунку 1
-
что соответствует изменение температуры на y1 ребре пластины согласно рисунку 1
С учетом выше описанных условий стандартизирующая функция примет следующий вид:
![]()
4 РАСЧЕТ ВЫХОДНОЙ ВЕЛИЧИНЫ
Для определения вида
статической характеристики воспользуемся функцией Грина: 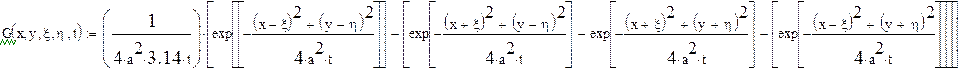
Для этого первоначально произведем расчет выходной вылечены по формуле:
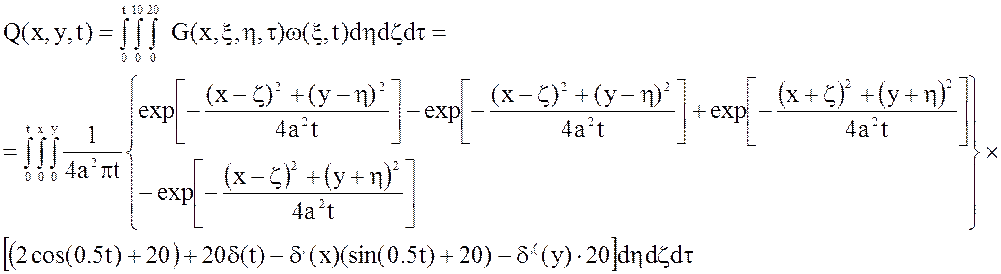
Воспользуемся свойствами ![]() – функции и для облегчения расчета
разобьем сложный интеграл на более простые получим:
– функции и для облегчения расчета
разобьем сложный интеграл на более простые получим:
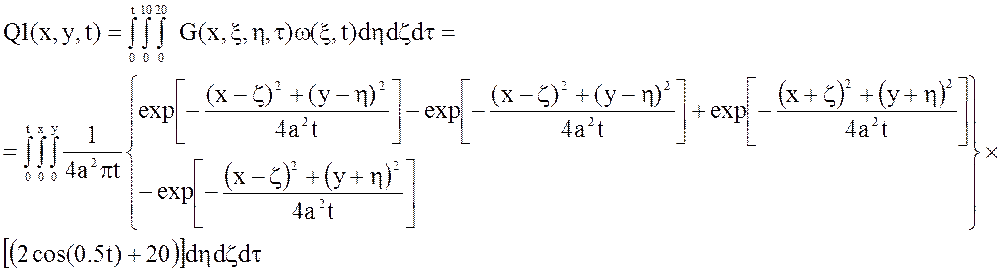
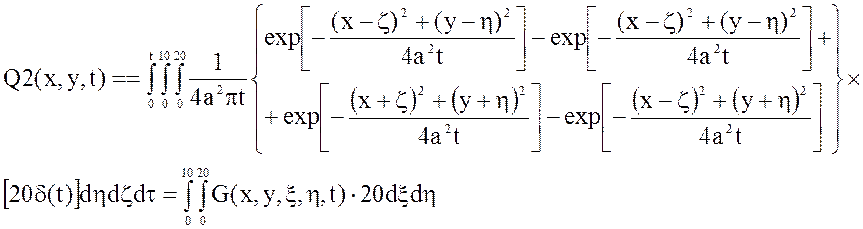
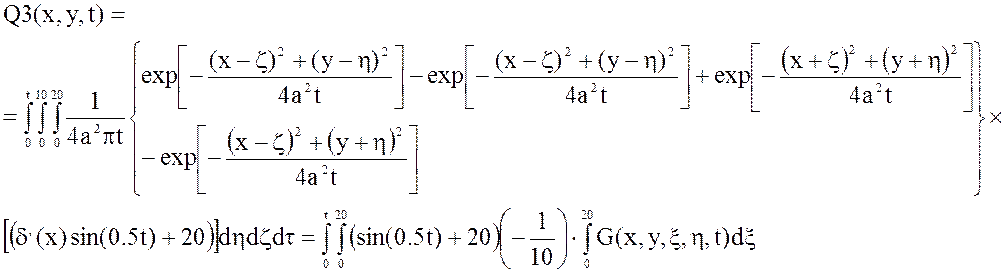
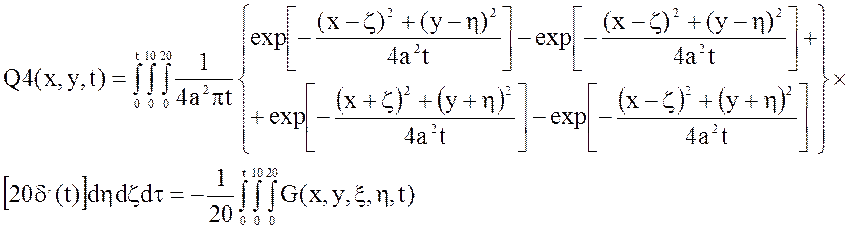
Сложим полученные интегралы и построим график зависимостей статической характеристики выходной величины при фиксированных значениях времени:
![]()
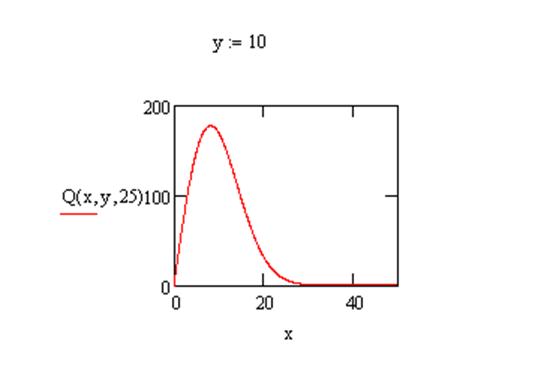
а
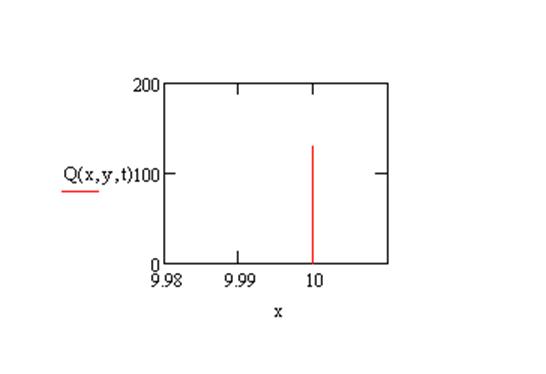
б
Рисунок -4. Статическая характеристика выходного сигнала: а - при фиксированном значении времени; б - при фиксированном значении координаты
5. РАСЧЕТ ИНТЕГРАЛЬНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ.
ПОСТРОЕНИЕ ЛОГАРИФМИЧЕСКИХ ХАРАКТЕРИСТИК
Найдем изображение по Лапласу стандартизирующей функции.
![]()
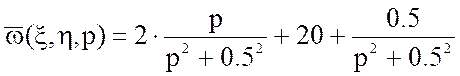
Выделим в явном виде компоненту входной координаты.
![]()
Выражение для ![]() имеет следующий вид:
имеет следующий вид:
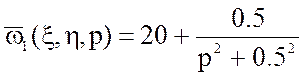
Интегральная передаточная функция определяется выражением
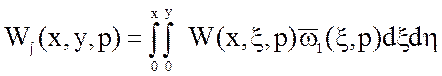
Проведя интегрирование и все преобразования, получим следующее выражение для интегральной передаточной функции:
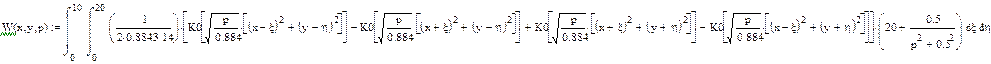
Для построения ЛАЧХ в полученной интегральной передаточной функции заменим р на jω и затем воспользуемся формулой:
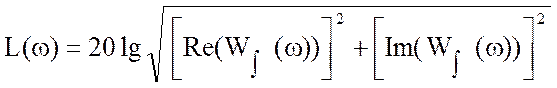
Выполним расчет и построение ЛАЧХ с
помощью программы Matchcad 2000, задав произвольно необходимые параметры:
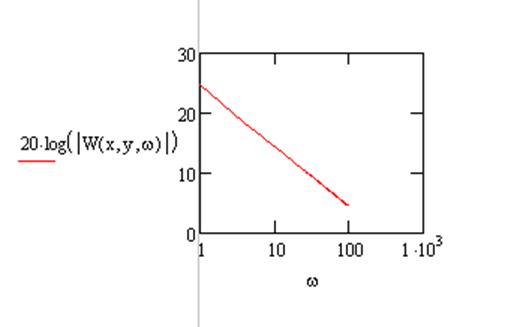
Рисунок 5- ЛАЧХ.
6.МОДЕЛИРОВАНИЕ PDE
Начертим изображение пластины в графическом окне PDETool таким образом, чтобы стороны были равны x1=10 и y1=20, где x1-размер по оси х, y1-размер по оси y.
Будем задавать граничные условия Дирихле u=0 на левой и правой сторонах. На
двух других сторонах примем условие Неймана ![]()
Укажем, что задача описывается уравнением параболического типа, и введем соответствующие коэффициенты:
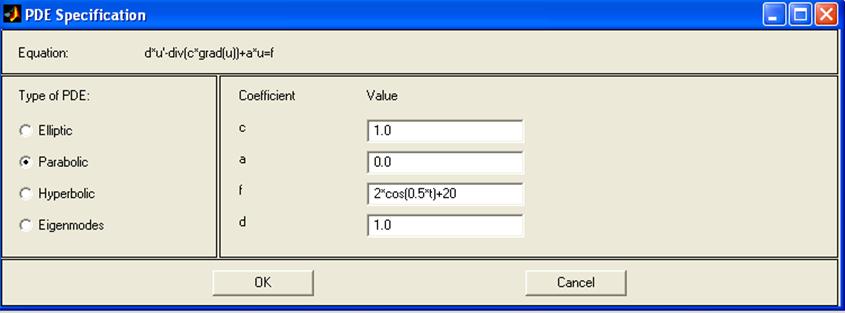
Рисунок 6 –Ввод параметров дифференциального уравнения
Зададим параметры решения и начальные условия – исходная температура пластины при t=20.
Для этого воспользуемся диалоговым окном «Solve Parametrs». Вначале выберем шаг и верхний
предел решения по времени. Для параметра Time введем стороку «0:0.1:10».Таким образом, расчет
выполнятся по времени в пределах t=0…10
с шагом ![]()
Начальные условия также записываются с учетом особенностей языка пакета MATLAB.
Начальная температура указывается строкой 20.
Относительную и абсолютную погрешность примем равными 0,01и 0,001, сохранив установленные по умолчанию значения.
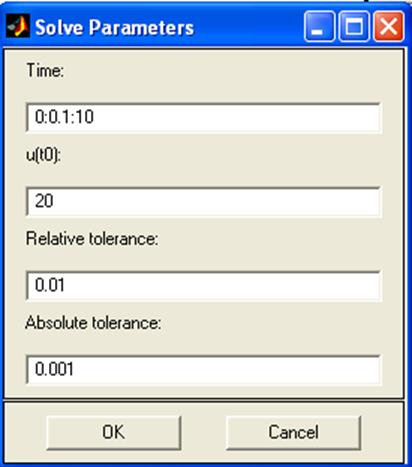
Рисунок 7 – Ввод параметров решения
Сформулируем сетку и настроим графические параметры решения с помощью диалогового решения с помощью окна «Plot Selection» представленную на рисунке 8:
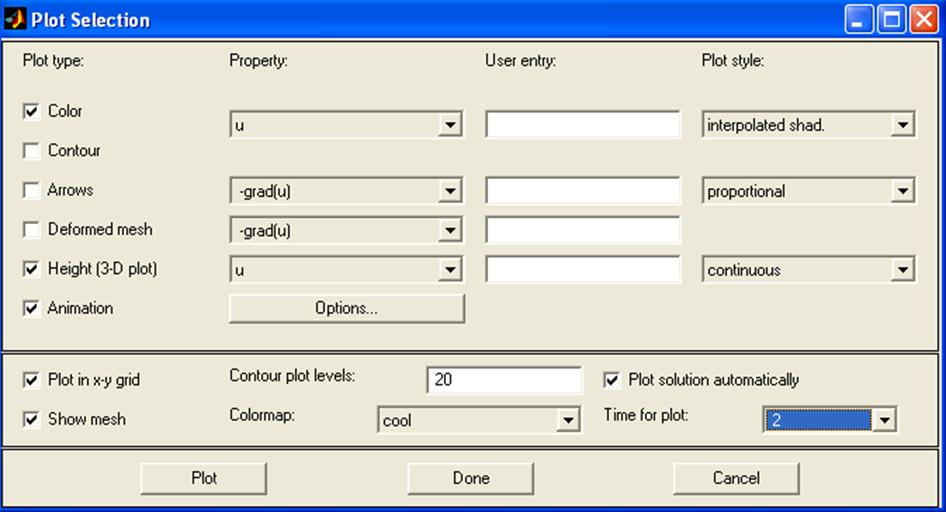
Рисунок 8- Параметры анимации.
Завершающий этап – запуск решения задачи. После окончания вычислений в графическом окне интерфейса PDETool отображается изменение температуры пластины в момент пластины в момент времени t=10, а в дополнительном окне – анимация изменения температуры пластины, представленный на рисунке 10 .
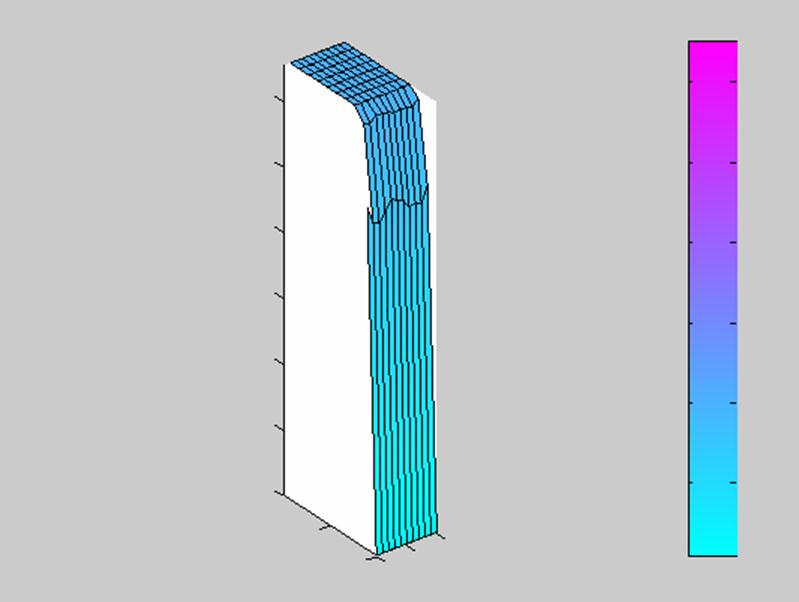
Рисунок 9- Анимация изменения температуры пластины
Изменяя граничные условия и параметры уравнения посмотреть, как изменяется выходная величина задачи на рисунке 10.
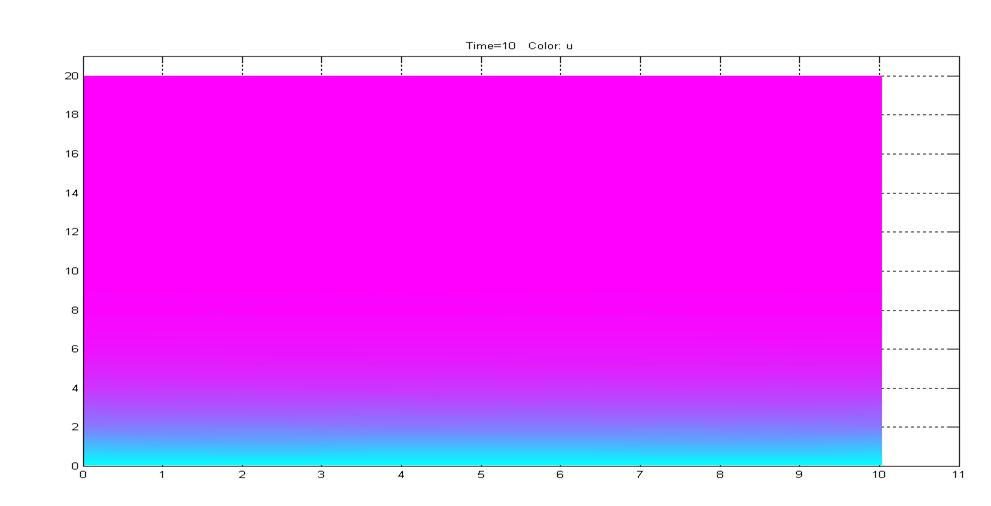
Рисунок 10. Модуль градиента выходной величины
ЗАКЛЮЧЕНИЕ
В данной курсовой работе был произведен расчет системы с распределенными параметрами: распределение температуры по алюминиевой пластине. В ходе расчетов было выявлено ниже следующее.
Система устойчива, имеет высокие качественные характеристики и достаточно высокий коэффициент усиления. Наша система не требует дальнейшей доработки. Это означает, что мы правильно подобрали начальные, граничные условия и дифференциальное уравнение для описания данной системы.
СПИСОК ЛИТЕРАТУРЫ
1. Тарасик В.П. Математическое моделирование технических систем: Учебник для вузов.-МН.: ДизайнПРО, 2004.
2. Тетрадь с лекциями по дисциплине «Сплошные среды и элементы с распределенными параметрами».
3. Арсенин В. Я. Математическая физика. – М. Наука, 1966.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.