Построение касательных к графику функции методом Ньютона (метод касательных)

Метод Ньютона

(метод касательных)

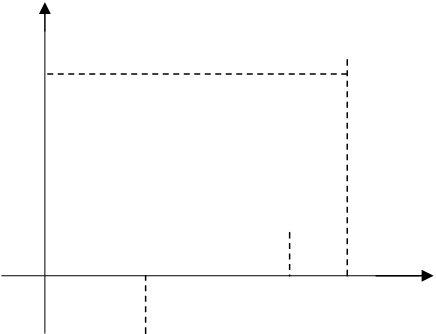
Геометрический смысл метода состоит в последовательном  построении касательных к графику функции y=f(x) и нахождении точек пересечения этих касательных с осью OX.

При этом не обязательно задавать отрезок [a,b], содержащий корень уравнения (2), а достаточно найти начальное приближение корня  x=x₀ .

 

   y                                     B             Уравнение касательной

f(x₀)                                      P₀                               к   кривой

                      _Y=F(x)               P₁                           y =f(x)  в  т.  P₀ (x₀; f(x₀)):

                                                                                         y – f(x₀) = f¢(x₀)(x-x₀);                                                                                       

                                                 P₂                                   y = f(x₀)+f¢(x₀)(x-x₀);      (5)

                                _{a               b     X}             Следующее  приближение

    0                                                              корня  x₁  ( y =o;  x=x₁ )

                 A                 x₂  x₁  x₀                          определим, как:

0  0=f(x₀)+f¢(x₀)(x₁-x₀);

x₁=x₀- f(x₀)/ f¢(x₀);

x₂=x₁- f(x₁)/ f¢(x₁);    и  т. д .

Формула для последовательных прближений к корню x^* имеет вид:

       x_n= x_n-1 - f(x_n-1)/ f¢(x_n-1);      где    f¢(x_{n -1})  0         (6)

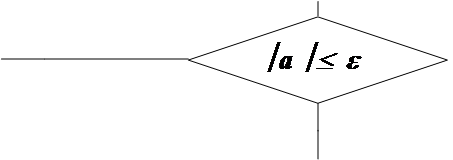
Для окончания итерационного процесса может быть использовано условие êf(x_{n -1})ê<e, либо условие близости двух последовательных приближений :         êx_n-x_n-1ê<e .

Для сходимости метода Ньютона достаточно, чтобы

         а) Отрезок [a,b] содержал единственный корень уравнения                              f(x)=0;

        б) функция f(x) имела на [a,b] непрерывные производные

 f¢(x) и f¢¢(x);

         в) производные  f¢(x) и  f¢¢(x)  не обращались в нуль на   [a,b];

         г) начальное приближение x₀  выбиралось так, чтобы выполнилось неравенство:       f(x₀)· f¢¢(x₀) > 0       (7)

Скорость сходимости в этом процессе выше, чем в других методах , хотя и больше объем вычислений.

Оценка погрешности этого метода имеет вид:

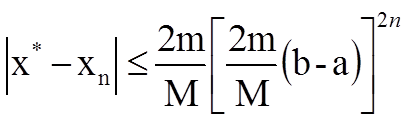
где  M = max ê f¢(x) ê;                    m = min ê f¢(x) ê;

           xÎ [a,b];                                     xÎ [a,b];

Сходимость улучшается при уменьшении величины:

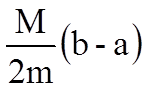                   [] < 1

Трудность метода – в выборе начального приближения.

Поэтому, целесообразно использовать смешенный алгоритм: Сначала применить сходящийся метод (например, метод деления отрезка пополам ), а после некоторого числа итераций – быстро сходящийся метод Ньютона.   

Пример решения методом Ньютона.

Дано:     Уравнение   3x-4Ln (x) –5 = 0.

             [ 0 ; 3,6 ]-отрезок,содержащий корень.

               Погрешность    e= 10 ^–3. Найти корень.

Решение

Проверяем условие сходимости :      f(x)*f¢¢(x) > 0 .

Из условия сходимости  выбираем  значение  x_{0 .}

Рассчетная формула :   x_n= x_n-1 - ;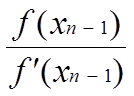

f(x) = 3x-4Ln (x) –5 ;         f¢(x) =3-4/x ; 

                                            f¢¢(x) = - (-4/x²) = 4/x² ;

f(3) =9-4*1,1-5=-0,4 < 0;

f¢¢(3) =4/9 > 0;

f(3,6) = 10,8 - 4*1,3 - 5 = 0,6 > 0 ;

 f¢¢(3 ,6) = 4/(3,6)² = 4/12,96 = 0,31 > 0;

f(3.6)*f ¢¢(3.6) > 0        Þx₀= 3,6 .

Программа метода Ньютона

Program      Kasat(input,output);

Uses Crt;

Var  a , d , x , x1 : real ; n : integer;

Const  eps = 0,001;

Function  power ( U : real ): real ;

   begin

   power := 3*U – 4* LN ( U ) – 5 ;

   end ;  { power }

Function  power 1 ( t : real ): real ;

   begin

   power1 := 3 – 4 / t;

   end ;  { power 1}

BEGIN

Clrscr;

x : = 3.6 ;    n : =0;

Repeat

n: = n + 1;

x1: = x – power ( x ) / power 1 ( x );

a: = x1 –x;

d: = power( x1 );

          Writeln( ` x = `, x1:8:1, ` d= `, d:8:1);

Writeln ( ` n = `, n );

x: =x1;

Until ABS ( a ) < = eps;

Repeat Until Keypressed ;

END.

Блок-схема метода

1

                                          Начало

 

2

                                            e = 10^-3

 

3

                                      n = 0; x = 3,6

 

4

                                          n = n + 1

 

5

 f(x)

 

6

                                               f ¢(x)

 

7

                                      x1=x-f(x)/f ¢(x)

 

8

                                         a = x1 - x

 

9

                                            d = f(x₁)

 

10

                                             x, d, n

 

11

                                             x = x1