Министерство образования РФ
Саратовский государственный технический университет
Балаковский институт техники, технологии и управления
Факультет вечерне – заочного обучения
Кафедра «Управление и информатика в технических системах»
«Математическое моделирование элементов систем управления»
Сухов Д.А.
Проверил
Бирюков В.П.
Задания к курсовому проекту:
Задание 1. Построить математическую модель, временные и частотные характеристики заданного элемента. Провести моделирование прохождения через элемент различных сигналов во временной области.
1.1. Построить математическую модель элемента в виде дифференциального
уравнения.
1.2.Построить передаточную функцию элемента по заданному каналу.
1.3.Используя вычеты получить выражения и построить графики весовой и
переходной характеристик.
1.4.Используя символьные вычисления MathCad , получим выражения и
построим графики весовой и переходной характеристик. Полученные
результаты сравнить с результатами п.3.
1.5.Рассчитать и построить графики амплитудно – частотной, фазо-частотной
характеристик, логарифмических частотных характеристик элемента.
Проверить в MathCad.
1.6. В Matlab составить схему и произвести моделирование прохождения
через исследуемый элемент ступенчатого , импульсного и
синусоидального сигнала. Полученные результаты сравнить с
результатами п.3,4.
1.7. Провести анализ прохождения через элемент случайного сигнала.
Задание 2. Построить теоретические и экспериментальные (имитационное моделирование) частотные характеристики звена первого порядка.
Задание 3. Для заданного типа электрического двигателя постоянного тока и параметров нагрузки построить дифференциальное уравнение и передаточную функцию электропривода по скорости при управлении по напряжению якоря. Провести моделирование различных режимов работы электропривода в MatLab.
3.1. Построить математическую модель электропривода в виде
дифференциального уравнения.
3.2. Построить передаточную функцию электропривода по каналу:
напряжение якоря - скорость электропривода.
3.3. Определить количественные оценки параметров математической модели.
3.4. Построить схему моделирования электропривода в MatLab, построить
переходные процессы:
- запуска электропривода при подаче на якорь номинального напряжения
- останова электропривода при снятии напряжения с якоря
- переходной процесс при пуске двигателя при U=0,4Uном и дальнейшем ступенчатом изменении напряжения до U=0,8Uном
Задание 1.
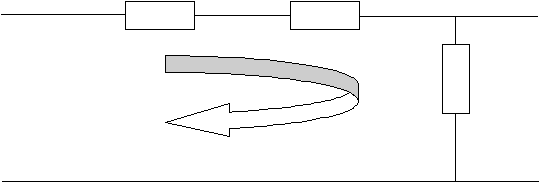
1.1. Построим математическую модель элемента в виде дифференциального уравнения.
R1L2
● ●
●
R2
U1 U2
I1
● ●
рис.1 «Эквивалентная схема объекта управления»
R1=374 [Ом]
R2=423 [Ом]
L1= 18 [Гн]
1.Зададимся направлением контурного тока I1.
2.Составляем уравнение по второму закону Кирхгофа для первого контура.
U1:=I1(R1+R2)+L1![]() I1
I1
3.По закону Ома
U2:=I1*R2 , тогда I1:=U2/R2
U1:=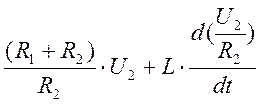
U1:=![]()
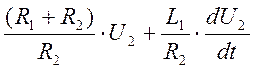
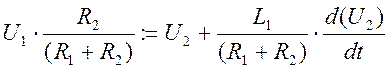
4.Запишем уравнение в стандартной форме, для чего выходную переменную перенесём в левую часть .
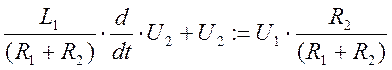
5.Обозначим
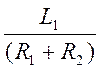 =
= ![]() ;
; 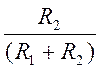 =
= ![]()
Тогда математическая модель в виде дифференциального уравнения будет иметь вид
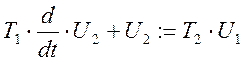
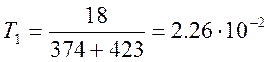
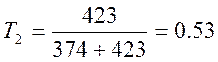
Дифференциальное уравнение имеет вид :
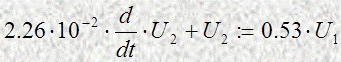
![]() 1.2. Построим передаточную функцию по
каналу U1U2
1.2. Построим передаточную функцию по
каналу U1U2
Преобразуем уравнение по Лапласу и запишем модель в виде передаточной функции как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной.
Для этого производную заменяем символом p , а переменные , зависящие от времени записываем как функции переменной p .
![]()
![]()
Отношение преобразования Лапласа от выходной переменной к преобразованию Лапласа от входной переменной
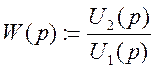
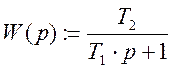
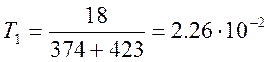
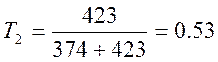
Передаточная функция имеет вид :
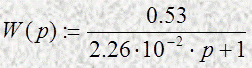
1.3. Используя вычеты получим выражения и построим графики
весовой и переходной характеристик элемента .
Операторный метод решения дифференциальных уравнений основан на использовании преобразования Лапласа, позволяющего преобразовать дифференциальное уравнение в алгебраическое, что упрощает их решение.
Последовательность нахождения реакции элементов систем управления на временной входной сигнал x(t):
- нахождение преобразования Лапласа x(p) от входного сигнала x(t)
- нахождение преобразования выходного сигнала y(p)=W(p)·x(p)
- нахождение временного выходного сигнала y(t) путем обратного преобразования Лапласа выходного сигнала y(p)
Последовательность обратного преобразования Лапласа от y(p)=M(p)/N(p):
- определяются корни характеристического уравнения выражения для y(p)
- в зависимости от вида корней записывается выражение для выходной переменной y(t).
1.3.1. Построим весовую характеристику системы. Преобразуем по Лапласу входной сигнал δ(t) – дельта функция Дирака.
![]()
Тогда выходной сигнал:
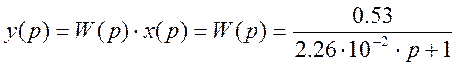
Найдем обратное преобразование Лапласа от y(p). Для этого необходимо найти корни характеристического уравнения.
![]()
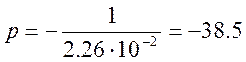
Т. к. корень простой (не комплексный), не нулевой, не кратный, то выражение для y(t) при t≥0 имеет вид:
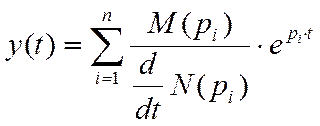
![]() ;
;
![]() ;
; 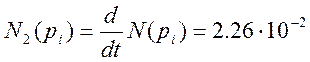
Весовая характеристика будет иметь вид:
![]()
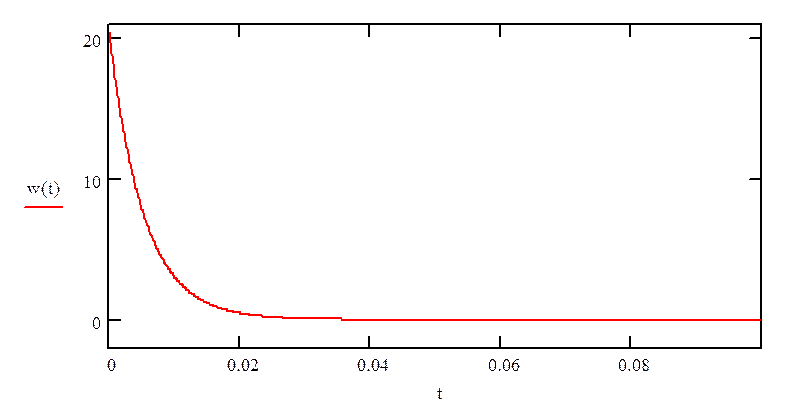
рис.2 «График весовой характеристики системы»
1.3.2. Построим переходную характеристику системы. Преобразуем по Лапласу входной сигнал 1(t) – функция Хевисайда.
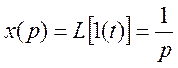
Тогда выходной сигнал:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.