Разработка математической модели, временных и частотных характеристик заданного элемента. Построение теоретических и экспериментальных (имитационное моделирование) частотных характеристик звена первого порядка, страница 2

                                        

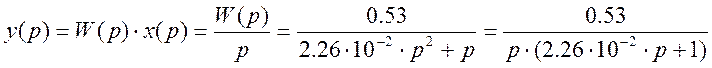
Найдем обратное преобразование Лапласа от y(p). Для этого необходимо найти корни характеристического уравнения.

                            

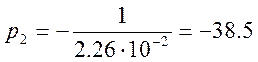
Т. к. корни простые (не комплексные),  не кратные, и имеется один нулевой корень, то выражение для y(t) при t≥0 имеет вид:

  

 

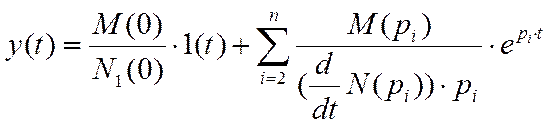
Переходная характеристика будет иметь  вид:

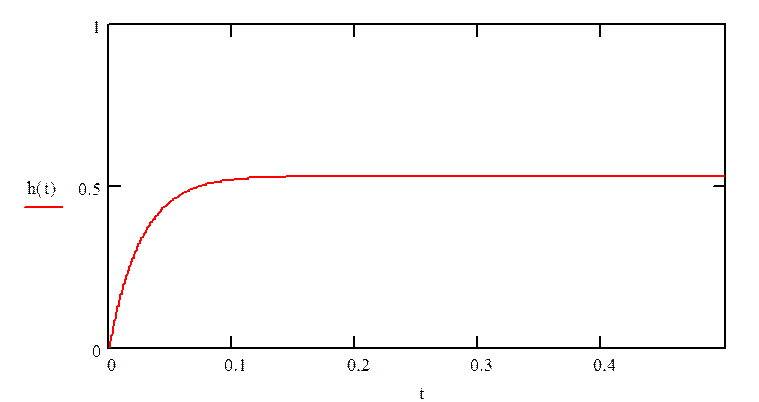
              рис.3 «График переходного процесса системы»

1.4.  Используя символьные вычисления MathCad , получим выражения

        и построим графики весовой и переходной характеристик.

рис.4 «График переходного процесса и весовой функции системы»

Как видно из графика, найденные значения весовой и переходной характеристик верны.

1.5.  Рассчитаем и построим графики амплитудно-частотной и фазо-

        частотной характеристик, логарифмических частотных

        характеристик элемента. Проверим в MathCad .

Последовательность нахождения частотных характеристик:

-  сделать замену в передаточной функции  p = j·ω

-  освободиться от мнимых чисел в знаменателе

-  раскрыть скобки и привести подобные члены, и разделить выражение в числителе на сумму действительного и мнимого полиномов

-  записать выражение для действительного и мнимого полиномов

-  записать выражение для логарифмической амплитудно-частотной характеристики

-  построить графики частотных характеристик.

Передаточная функция:

                           

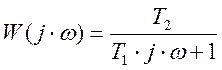
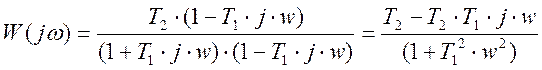
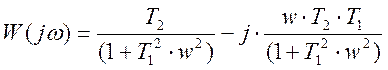
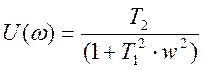
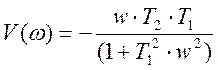
где    U(ω) – вещественная частотная характеристика

         V(ω) – мнимая частотная характеристика

Подставим значения коэффициентов:

      

 

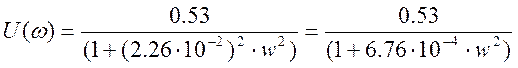
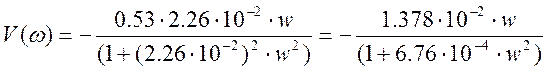
Построим амплитудно-частотную характеристику:

                           

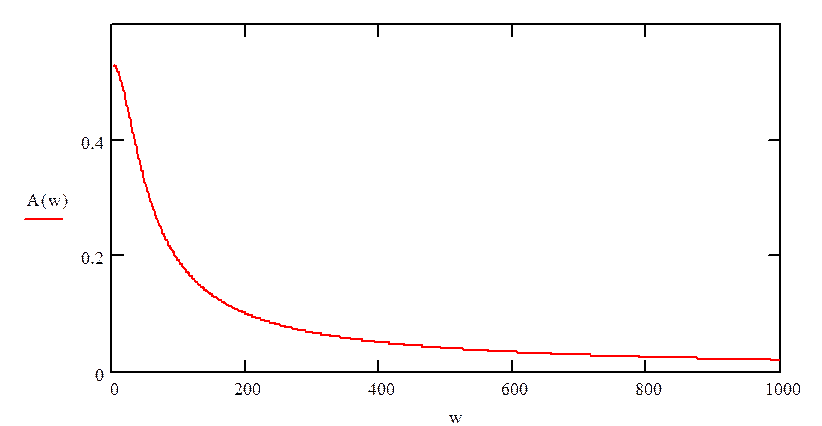
рис.5«График амплитудно-частотной характеристики»

Построим амплитудно-фазовую характеристику (годограф):

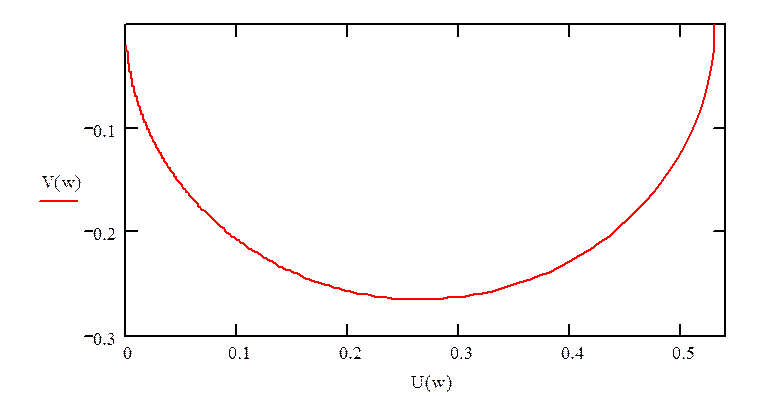
рис.6«Годограф»

Построим фазо-частотную характеристику:

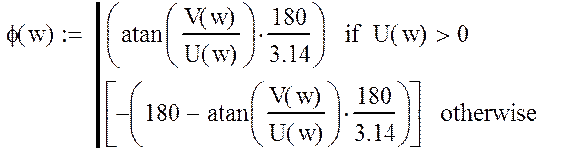
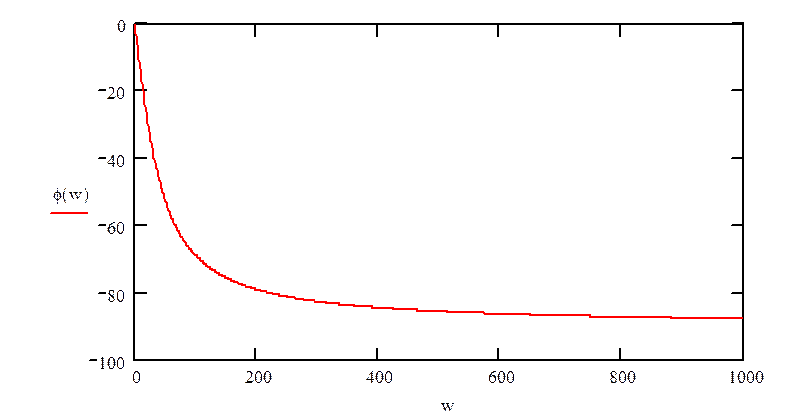
рис.7«График фазо-частотной характеристики»

Построим логарифмическую амплитудно-частотную характеристику:

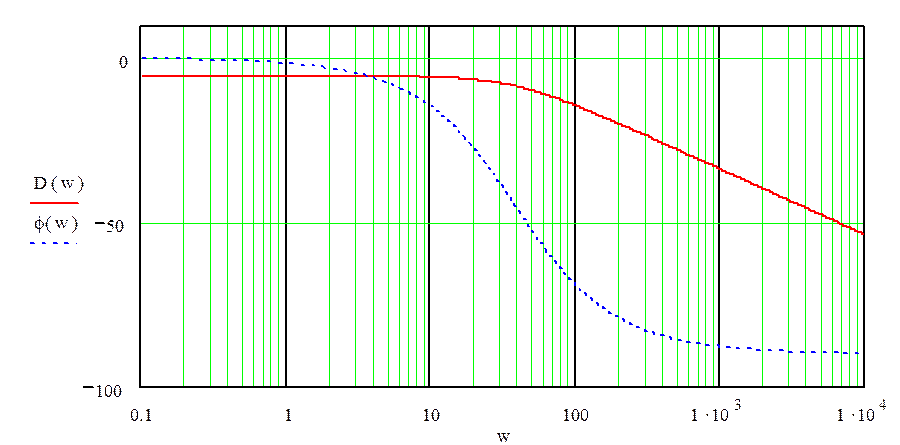
рис.8«График логарифмической амплитудно-частотной характеристики»

Проверим правильность расчетов частотных характеристик устройства с помощью MathCAD.

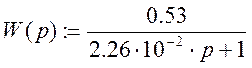
Запишем выражения для построения частотных характеристик с помощью встроенных функций MathCAD.

      A1(w) - амплитудно-частотная характеристика

рис.9«График амплитудно-частотной характеристики»

φ1(ω) - фазо-частотная характеристика   

рис.10«График фазо-частотной характеристики»

  логарифмическая амплитудно-частотная характеристика.

рис.11«График логарифмической амплитудно-частотной характеристики»

Проверка показала, что частотные характеристики объекта управления построены верно.

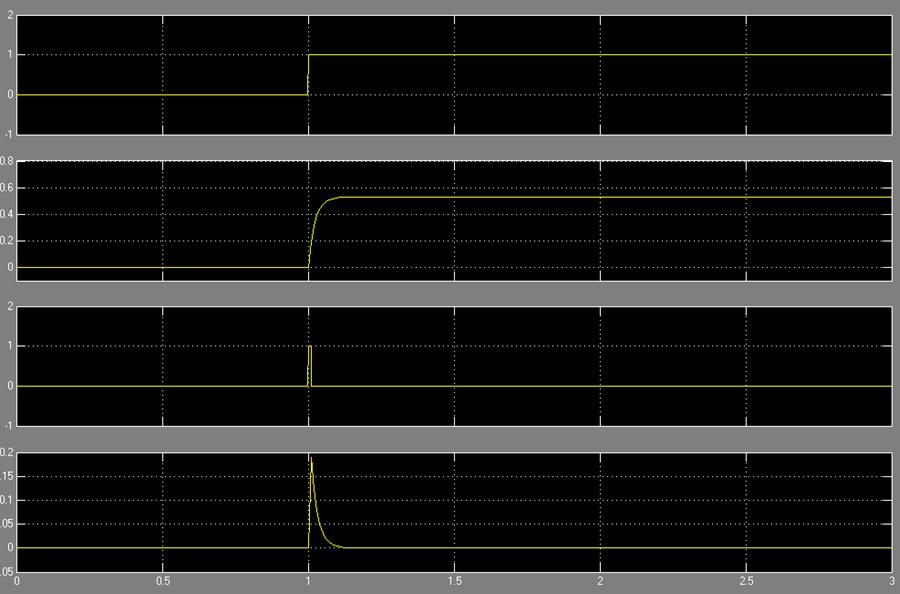
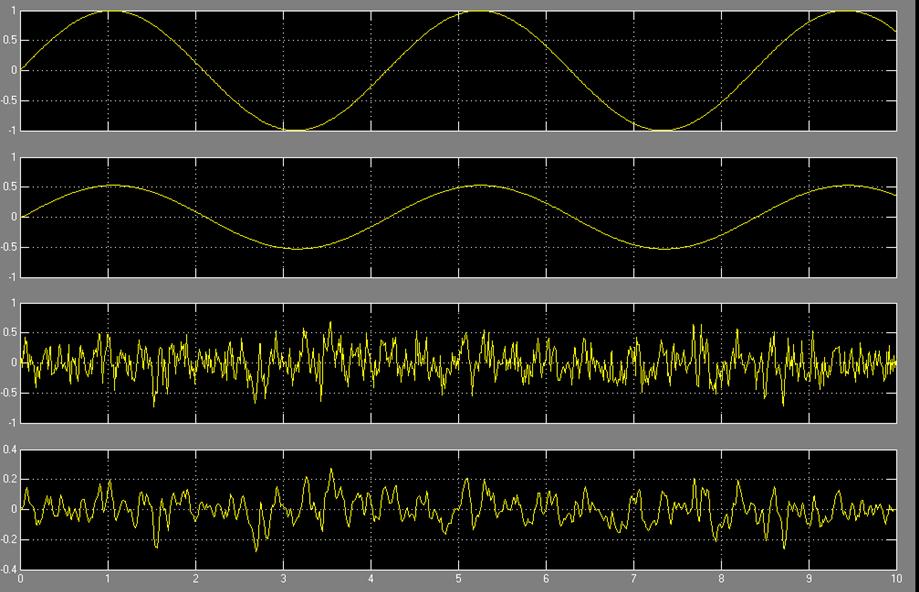
1.6. В Matlab составим схему и произведём моделирование прохождения через исследуемый элемент ступенчатого , импульсного и синусоидального сигнала .

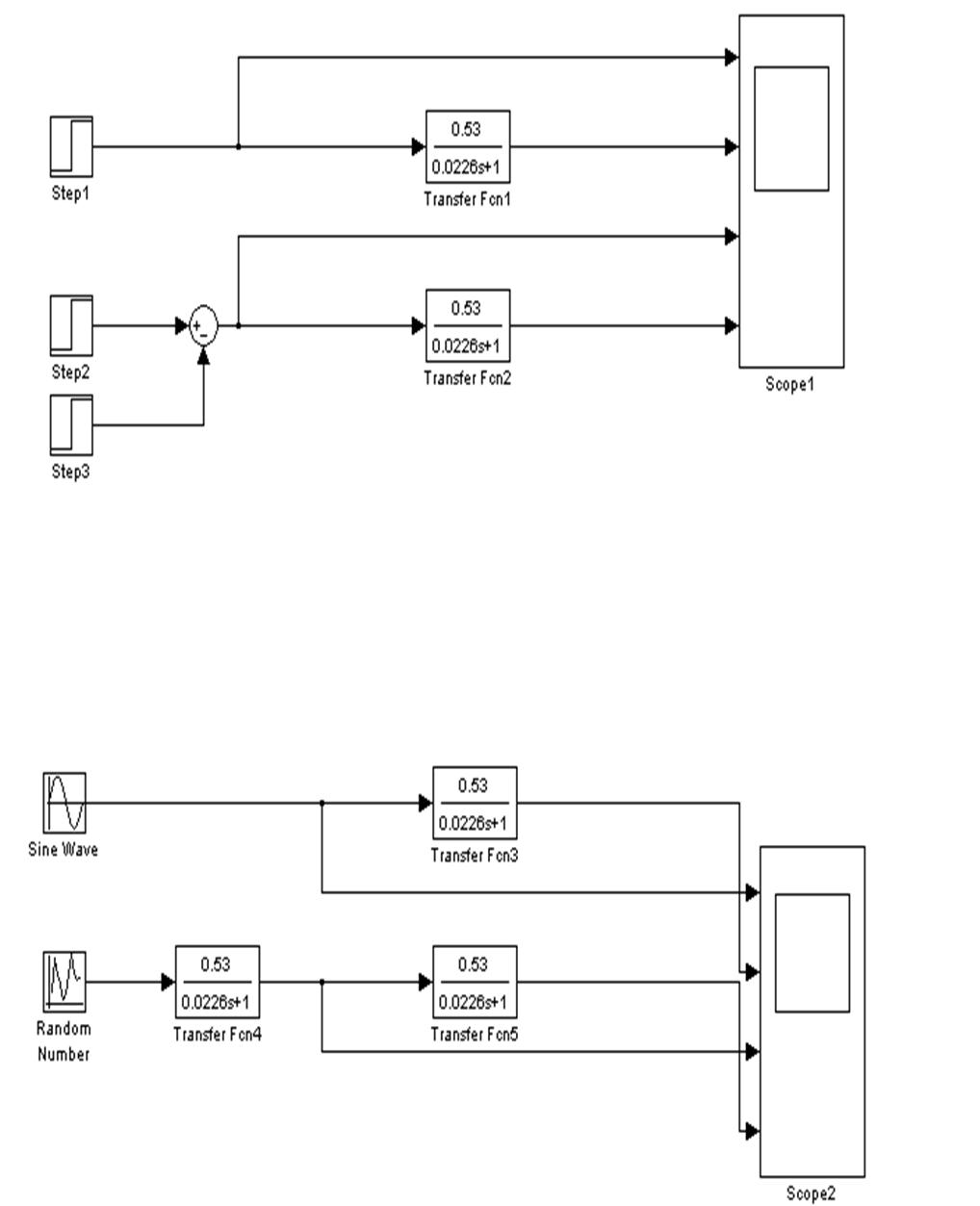
                                                   Осциллоскоп №1

                                                            Осциллоскоп №2

Задание 3.

3.1. Найдем передаточную функцию электропривода по каналу  «напряжение якоря - скорость электропривода»

Электропривод можно разделить на две составляющие: электрическую и механическую части. Электрическая часть описывается уравнениями Кирхгофа, а механическая через моменты инерции, нагрузки и сопротивления.

Запишем уравнение для механической части электропривода:

                  

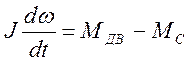
 где Мдв – момент на валу двигателя

                         Мс – момент сопротивления

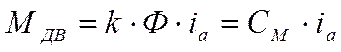
Запишем уравнение для электрической части электропривода:

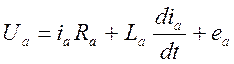
где     еа – противоЭДС в якоре

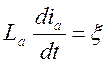          - присутствует только при изменении тока в якоре

 

В данном случае инерционность системы определяется моментом инерции J. В связи  с этим время переходных процессов мало, поэтому =0.

                 

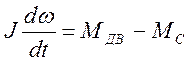             где Мс = const

Запишем систему уравнений в отклонениях:

 

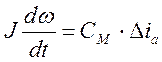
                                            (1)

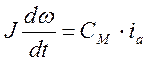            (2)

Из уравнения (2) выразим ia и подставим в (1):

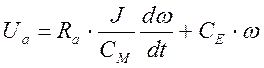  (3)

Разделив уравнение (3) на СE, получим:

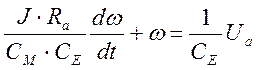
Введем обозначения:

                                  

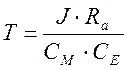
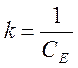
Получим дифференциальное уравнение, описывающее электропривод:

 

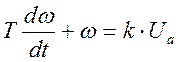
Следовательно, электропривод является апериодическим звеном первого порядка.

3.2. Найдем передаточную функцию электропривода.

Преобразуем уравнение по Лапласу.

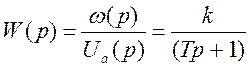   - передаточная функция   электропривода по каналу «напряжение якоря – скорость электропривода»

3.3. Определим количественные оценки параметров математической  

       модели электропривода.

 Исходные данные:

1.  Тип двигателя ДМП 11 (постоянного тока)

2.  Номинальная мощность Рн = 2,8  [кВт]

3.  Номинальное напряжение якоря Uн = 220  [В]

4.  Номинальный ток якоря Iн = 14,5  [А]

5.  Номинальный крутящий момент Мн = 14,95   [н·м]

6.  Максимальная скорость вращения n = 1790   [об/мин]

7.  Момент инерции якоря Ja = 0,04    [кг·м²]

8.  Сопротивление обмотки якоря Ra = 7,59  [Ом]

9.  Момент инерции нагрузки Jн = 105    [кг·м²]

10. Коэффициент редукции Кред = 120

Рассчитаем коэффициент противоЭДС:

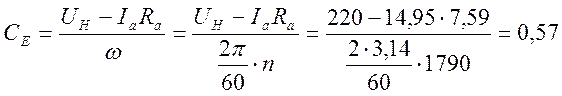 [В·с/рад]

Рассчитаем коэффициент момента:

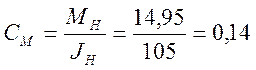  [кгм/А]

Найдем полный момент инерции:

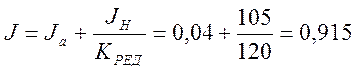  [кг·м²]

Найдем коэффициенты передаточной функции электропривода:

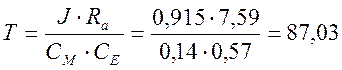  [с]

                             

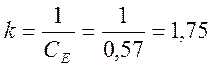
Тогда передаточная функция примет вид:

                                

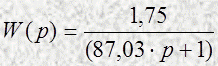
3.4. Построим графики переходных процессов электропривода.

Решив дифференциальное уравнение, описывающее электропривод, получим уравнение движения эл. двигателя при начальной скорости ω0 при входном сигнале Ua.

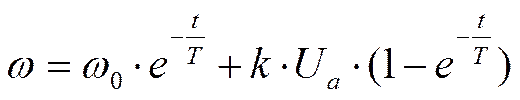
Рассмотрим три режима работы электропривода:

-  «пуск» - начальная скорость ω0 = 0 [рад/с], входное напряжение Ua = Uн = 47  [В]

-  «останов» - начальная скорость ω0 = ωн = 62,8 [рад/с], входное напряжение Ua = 0 [В]

-  «переход» - переходной процесс при пуске двигателя при Ua = 0,4Uн и дальнейшем ступенчатом увеличении напряжения до Ua = 0,8Uн.