














СОДЕРЖАНИЕ
ИСХОДНЫЕ ДАННЫЕ 2
1.Построение математической модели ОУ в пространстве состояния 3
2. Построение сигнального графа и структурной схемы системы 6
3. Нахождение передаточной функции системы по формуле Мейсона 7
4. Анализ устойчивости системы по критерию Ляпунова 9
5. Определение прямых оценок качества системы 10
6. Синтез формирующего фильтра 13
7. Оценка качества эквивалентной схемы по переходной функции 17
ВЫВОД 19
Список используемой литературы 20
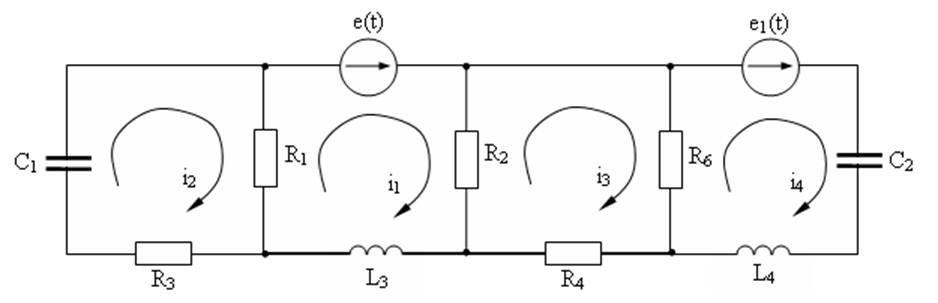
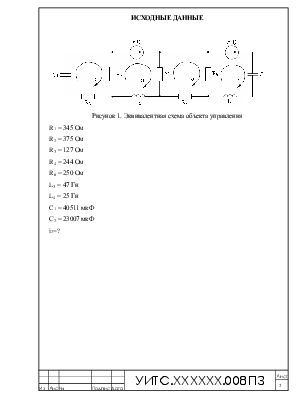
Рисунок 1. Эквивалентная схема объекта управления
|
R1 = 345 Ом R2 = 375 Ом R3 = 127 Ом R4 = 244 Ом R6 = 250 Ом L3 = 47 Гн L4 = 25 Гн C1 = 40511 мкФ С2 = 23007 мкФ |
i2=?
1. ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОУ В ПРОСТРАНСТВЕ СОСТОЯНИЯ
 e(t) i4
e(t) i4
Рисунок 2. Структурная схема объекта управления
Cоставим уравнения по 2-му закону Кирхгоффа для контуров:
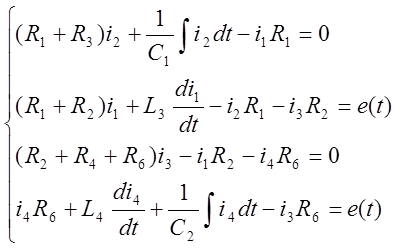 (1)
(1)
В системе уравнений (1) следует избавиться от всех интегралов, продифференцировав в данном случае первое и четвертое уравнения этой системы:
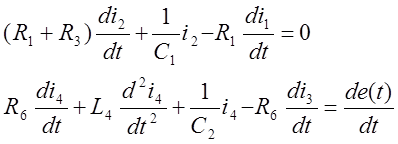
Используя метод условного интегрирования, вводим фиктивные переменные, равные элементам, взятым из уравнений на 1 или более порядков ниже.
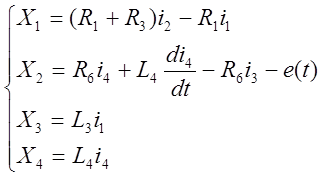 (2)
(2)
Находим производные по времени от фиктивных переменных и, применяя предыдущие уравнение, выражаем зависимостями от токов и фиктивных переменных.
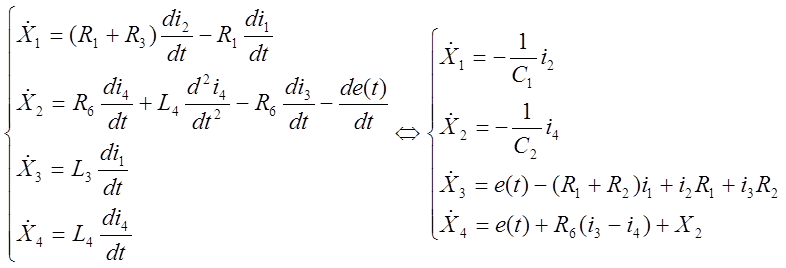 (3)
(3)
Из систем уравнений (1) - (3) найдем выражения для токов через фиктивные переменные:
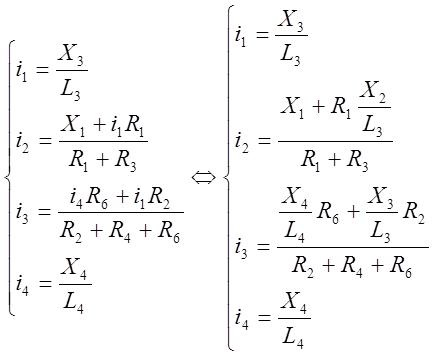 (4)
(4)
Подставим числовые данные в систему (4) и найдем i1, i2, i3, i4:
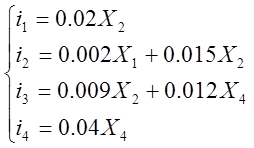
Полученные значения токов
подставим в систему (3) и найдем ![]() ,
, ![]() ,
, ![]() ,
,
![]() , дополнив систему выражением для
выходной величины:
, дополнив систему выражением для
выходной величины:
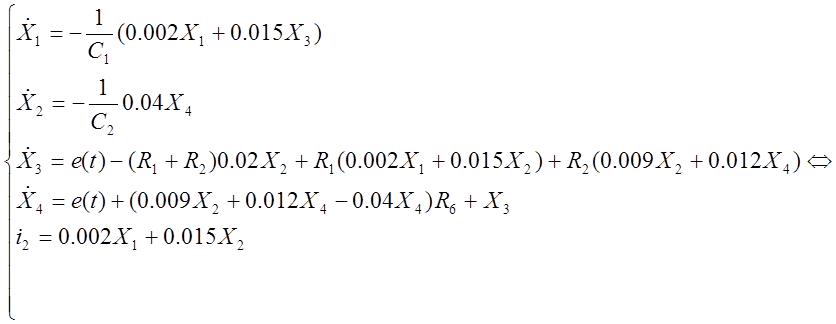
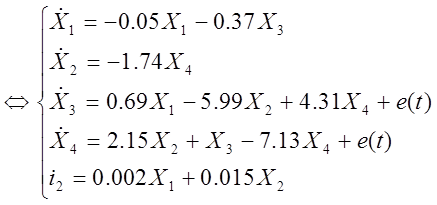
По полученной системе уравнений и уравнению для выходной величины
объекта регулирования запишем математическую модель в нормальной форме Коши:
![]() – уравнение наблюдения;
– уравнение наблюдения;
![]() – уравнение выходной величины
объекта,
– уравнение выходной величины
объекта,
где A, B, C, D – матрицы, Х – матрица внутренних переменных, U – матрица входных переменных (в данном случае ЭДС).
Матрицы будут иметь вид:
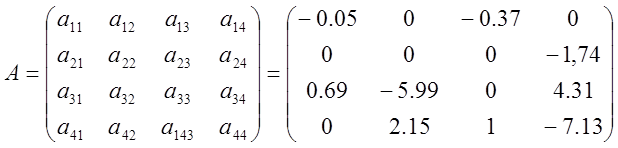
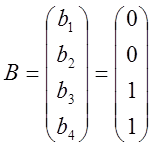
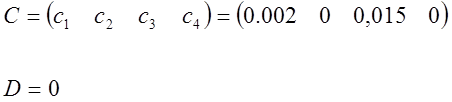
Получаем математическую модель в пространстве состояний:
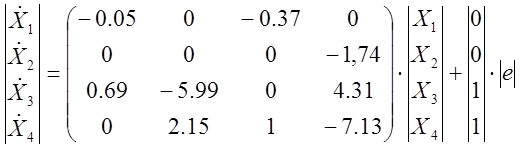
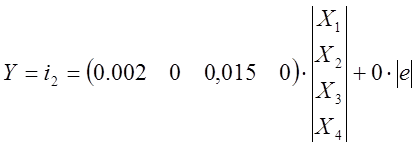
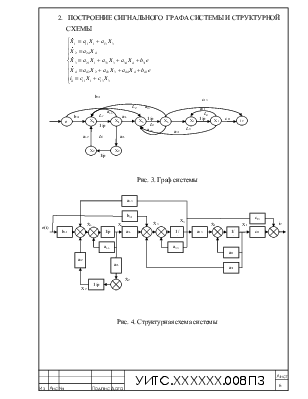
2. ПОСТРОЕНИЕ СИГНАЛЬНОГО ГРАФА СИСТЕМЫ И СТРУКТУРНОЙ СХЕМЫ
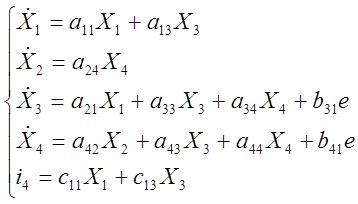
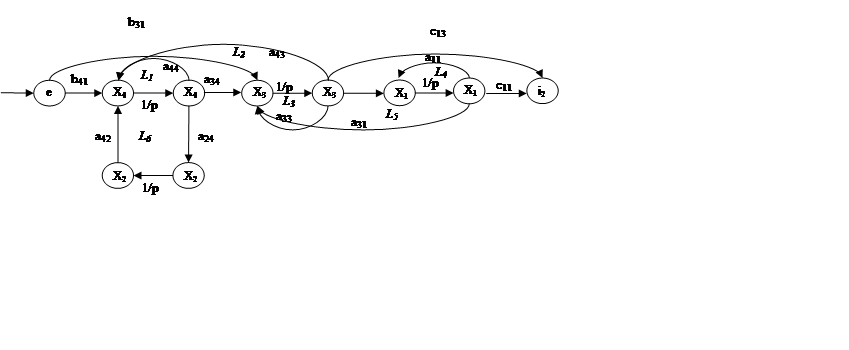
Рис. 3. Граф системы
|
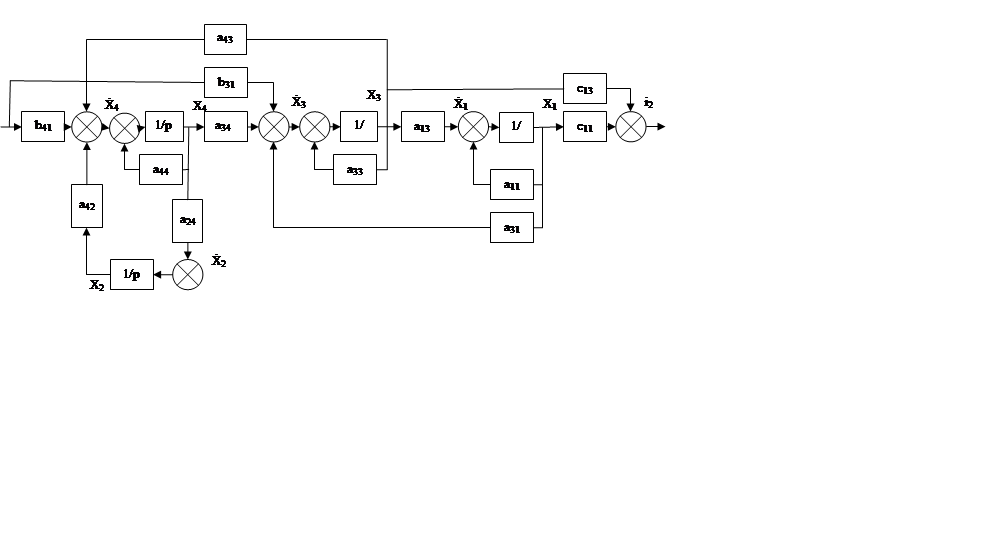
Рис. 4. Структурная схема системы
3. НАХОЖДЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СИСТЕМЫ ПО ФОРМУЛЕ МЕЙСОНА
Найдем передаточную функцию объекта управления непосредственно из графа системы по формуле Мейсона, которая имеет вид:
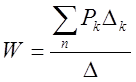 ;
; 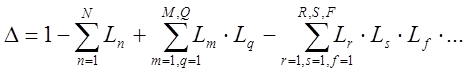 ,
,
где k – количество прямых возможных путей от входа к выходу;
∆ – определитель графа;
Pk – коэффициент передачи k-го пути от входа к выходу;
∆k – определитель всех касающихся контуров при удалении k-го пути;
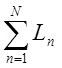 – сумма коэффициентов передачи всех
отдельных контуров;
– сумма коэффициентов передачи всех
отдельных контуров;
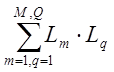 – сумма всех возможных произведений
из двух не касающихся контуров;
– сумма всех возможных произведений
из двух не касающихся контуров;
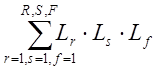 – сумма всех возможных комбинаций из
трех не касающихся контуров.
– сумма всех возможных комбинаций из
трех не касающихся контуров.
Запишем уравнения всех прямых путей от входа к выходу:
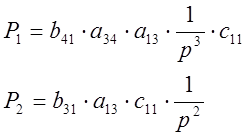
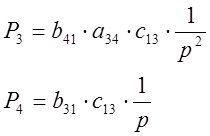
Определим все замкнутые контуры и запишем их уравнения:
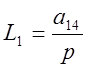
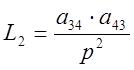
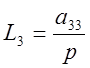
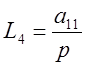
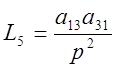
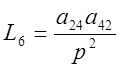
Запишем выражение для определителя системы:
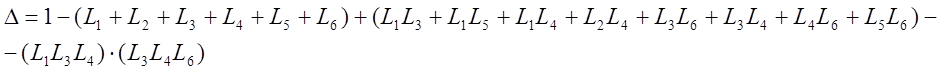
Запишем определители путей:
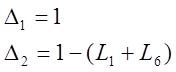
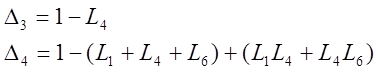
Запишем и посчитаем выражение передаточной функции, подставив все найденные величины:
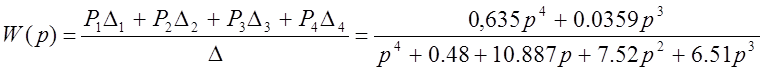
4. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМЫ ПО КРИТЕРИЮ ЛЯПУНОВА
Проведём оценку устойчивости САУ по критерию Ляпунова, для чего найдем корни характеристического уравнения:
![]()
![]()
![]()
![]()
![]()
Так как все 4 корня характеристического уравнения находятся в левой части, то согласно критерию устойчивости по Ляпунову система является устойчивой.
5. ОПРЕДЕЛЕНИЕ ПРЯМЫХ ОЦЕНОК КАЧЕСТВА СИСТЕМЫ
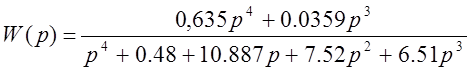
Определение временных и частотных характеристик по передаточной функции.
Найдем переходную ![]() функцию, она равна обратному
преобразованию Лапласа от
функцию, она равна обратному
преобразованию Лапласа от ![]() , т.е.
, т.е.
![]()
|
|
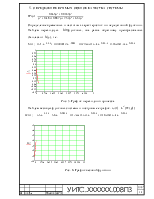
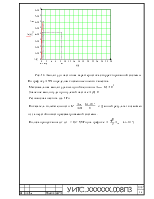
Рис. 5. График переходного процесса
Найдем весовую функцию
системы и построим ее график. ![]()
![]()
|
|
Рис. 6. График весовой функции
Определим частотные характеристики системы. Приведем передаточную функцию системы к частотной форме записи, заменив оператор Лапласа р на jω:
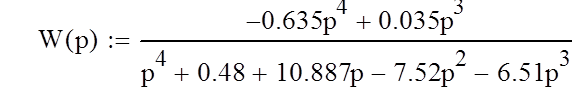
Амплитудо-частотная характеристика находится по формуле:
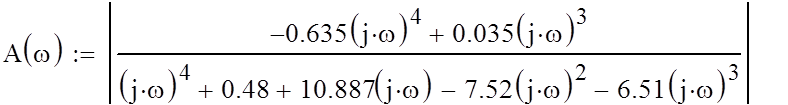
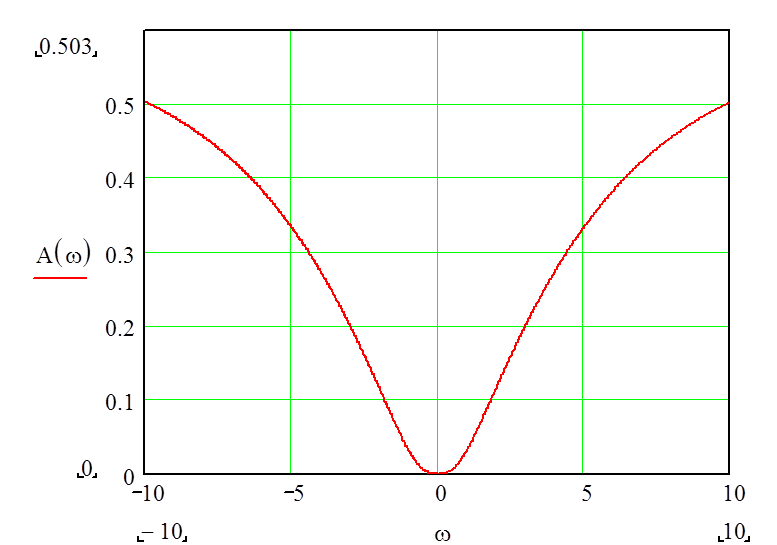
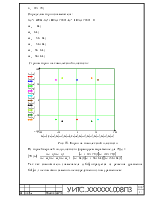
Рис. 7. График амплитудо-частотной характеристики
Найдем фазо-частотную характеристику и построим ее график.
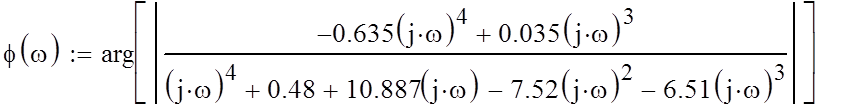
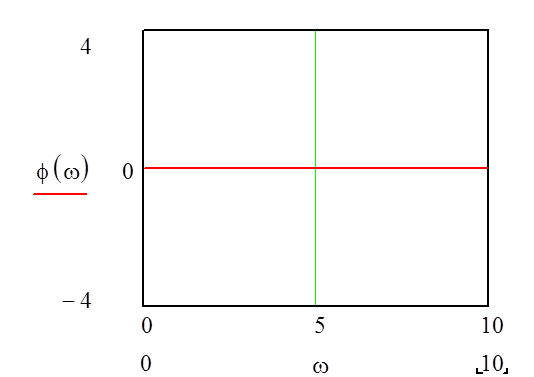
Рис. 8. График фазо-частотной характеристики
По переходной функции определим прямые оценки качества системы:
Перерегулирование
По графику видно, что система является неустойчивой, поэтому прямые оценки качества провести в этом случае невозможно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.