Задание
Вариант № 23
|
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
L1 |
L2 |
L3 |
L4 |
C1 |
C2 |
|
335 |
389 |
114 |
219 |
– |
199 |
– |
30 |
50 |
23 |
– |
17180*10-6 |
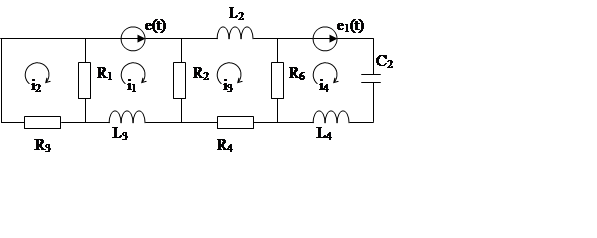 |
e(t),e1(t) – входные величины
i3 – выходная величина
1. Построение математической модели управления
1. 1 Построение математической модели для электрической схемы
Постоим математическую модель объекта управления в пространстве состояния. Структурная схема объекта управления:
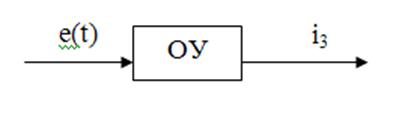
В схеме четыре элемента,
запасающих энергию ![]() следовательно математическая модель
должна быть четвертого порядка.
следовательно математическая модель
должна быть четвертого порядка.
1.2 Построение математической модели:
Составляем четыре уравнения по второму закону Кирхгофа для контуров и найдем систему уравнений, описывающую объект управления по методу контурных токов:
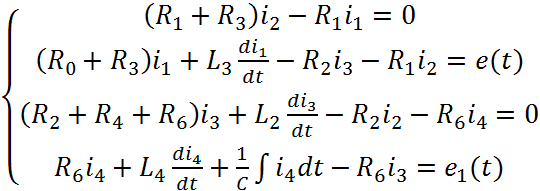 (1)
(1)
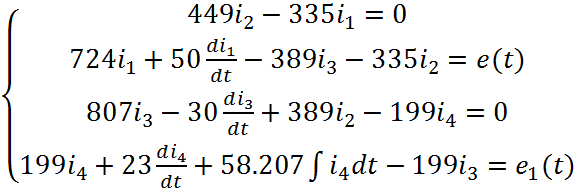 (2)
(2)
В исходной системе уравнений следует избавиться от всех интегралов, продифференцировав уравнения.
Избавляемся от интеграла в последнем уравнении системы (2):
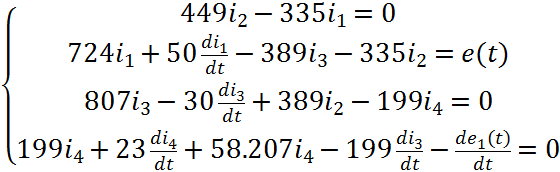 (3)
(3)
Используя метод условного интегрирования, следует ввести фиктивные переменные, равные элементам, взятым из уравнении, но на 1 или более порядков ниже.
В нашем случае, используя метод условного интегрирования, вводим фиктивные переменные, равные элементам, взятым из уравнения (3) на 1 и 2 порядка ниже и из 2-го и 3-го уравнений системы (2):
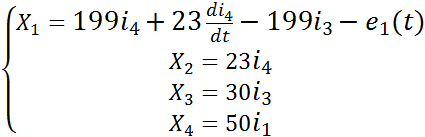 (4)
(4)
Находятся производные по времени от фиктивных переменных и, применяя предыдущие уравнения, выражаются зависимостями от токов фиктивных переменных.
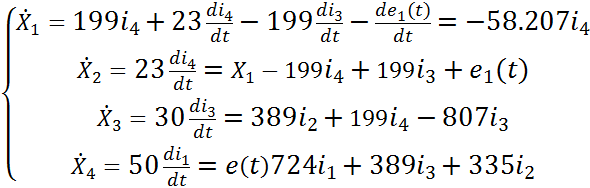 (5)
(5)
Из системы (4) и первого уравнения системы (2) выразим токи таким образом, чтобы они зависели только от фиктивных переменных.
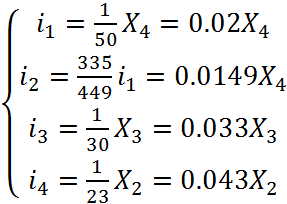 (6)
(6)
Полученные выражения
токов подставим в систему (5) и дополним выражением для выходной величины, в
результате получим: 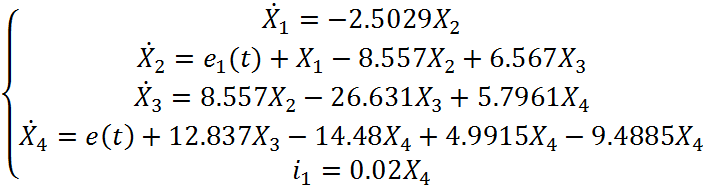 (7)
(7)
По полученной системе уравнений и уравнению для выходной величины объекта регулирования записывается математическая модель в нормальной форме Коши:
![]() -уравнение наблюдения.
-уравнение наблюдения.
![]() -уравнение выходной величины объекта,
-уравнение выходной величины объекта,
где A,B,C,D – матрицы;
Х – матрица внутренних переменных;
U – матрица входных переменных, в данном случае U – ЭДС.
В данном случае матрицы будут иметь вид:
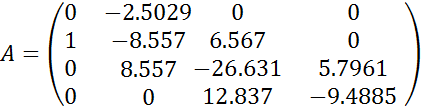
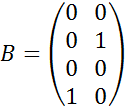
![]()
![]()
Получаем математическую модель в пространстве состояний
1.3 Построение графа системы и нахождение передаточной функции
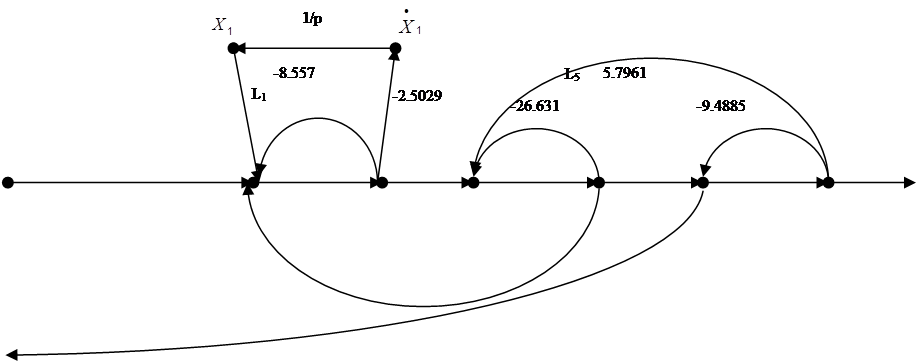 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
 |
||||||||||||||||
|
Рис.1 Граф
Перейдем от графа к структурной схеме
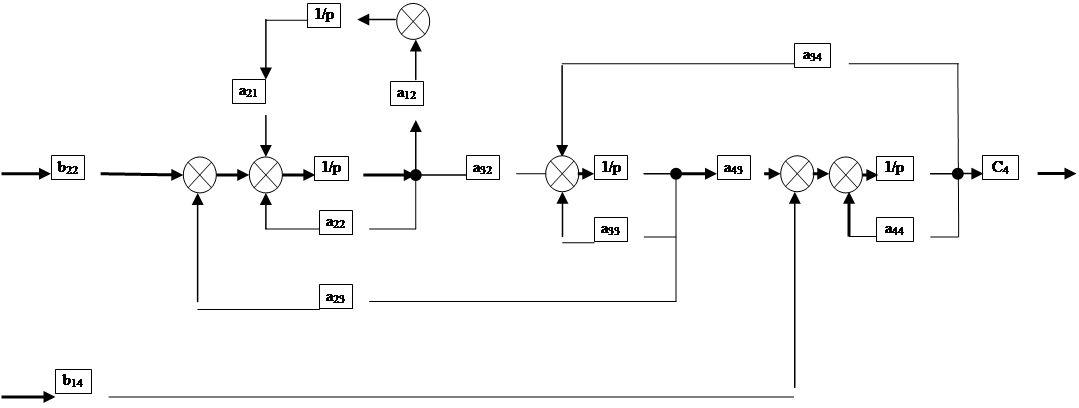
Рис 2. Структурная схема
С помощью формулы Мейсона найдем передаточную функцию системы:
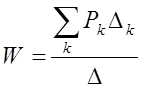 ,
,
Где
к – количество возможных прямых путей от входа к выходу
![]() – определитель графа
– определитель графа
Рк – коэффициент передачи к-того пути от входа к выходу
![]() – определитель всех
касающихся контуров при удалении к – того пути
– определитель всех
касающихся контуров при удалении к – того пути
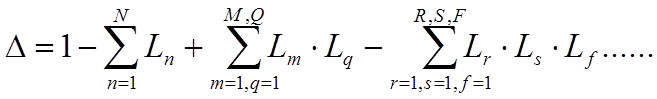
Где
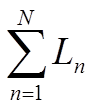 – Сумма коэффициентов
передачи всех отдельных контуров
– Сумма коэффициентов
передачи всех отдельных контуров
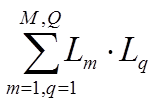 – сумма всех возможных произведений
из 2-х не касающихся контуров
– сумма всех возможных произведений
из 2-х не касающихся контуров
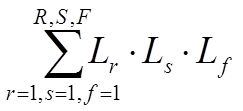 – сумма всех возможных комбинаций из 3-х не касающихся
контуров
– сумма всех возможных комбинаций из 3-х не касающихся
контуров
Определим прямые пути:
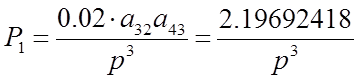
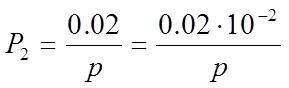
В системе имеется 6 замкнутых контуров:
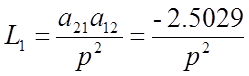
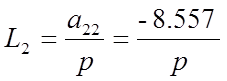
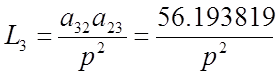
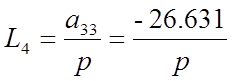
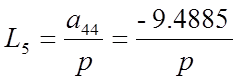
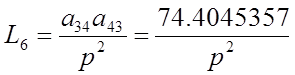
Находим определитель графа :
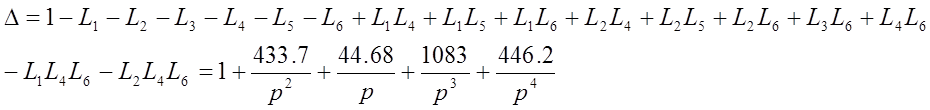
Находим определители путей:
![]()
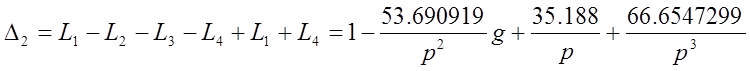
Запишем передаточную функцию:
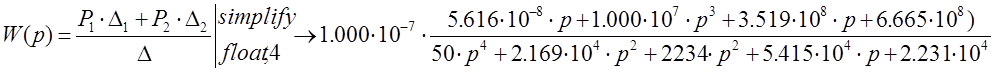
1.4 Прямые и косвенные оценки качества
По полученной передаточной функции найдем выражения для весовой и переходной характеристик, АЧХ и ФЧХ, построим графики.
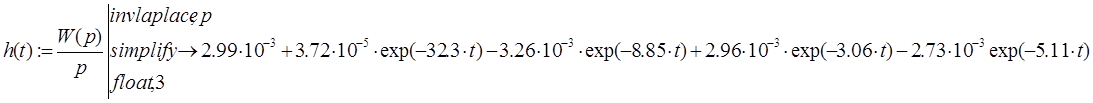
Рис.3 График переходной функции
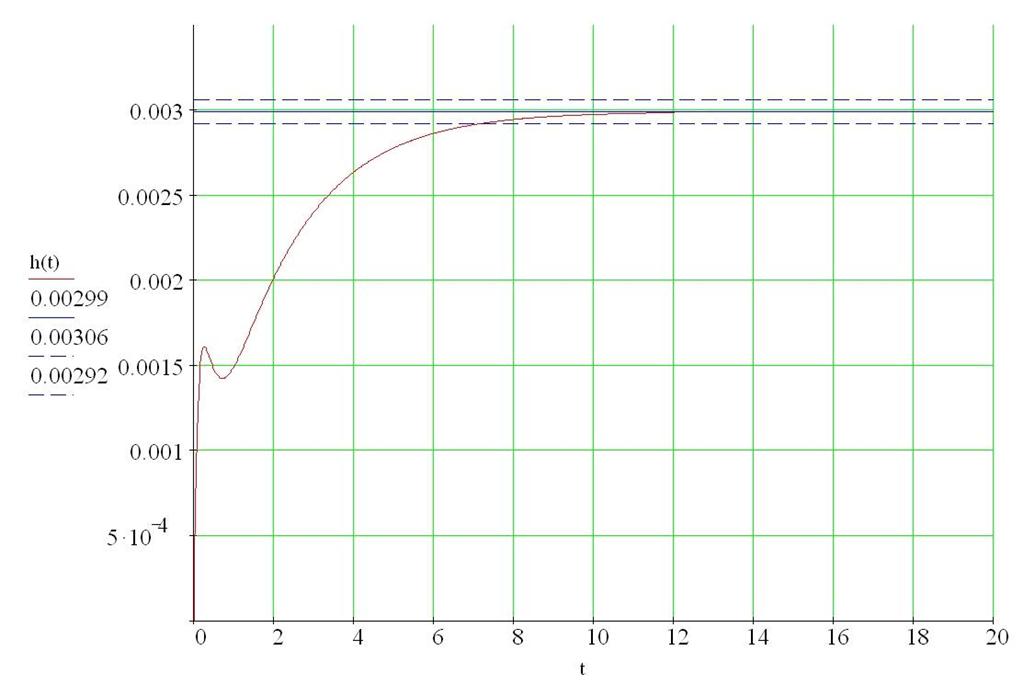
h(t)уст = 0,00299 – установившееся значение переходного процесса
h(t)max = 0,00299 – максимальное значение переходного процесса
tпп= 7 с – Время переходного процесса
tсог= 12 с – Время первого согласования
tнар= 12 с – Время нарастания
n = 0 – Количество колебаний
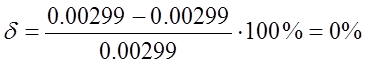 – Перерегулирование
– Перерегулирование
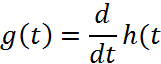
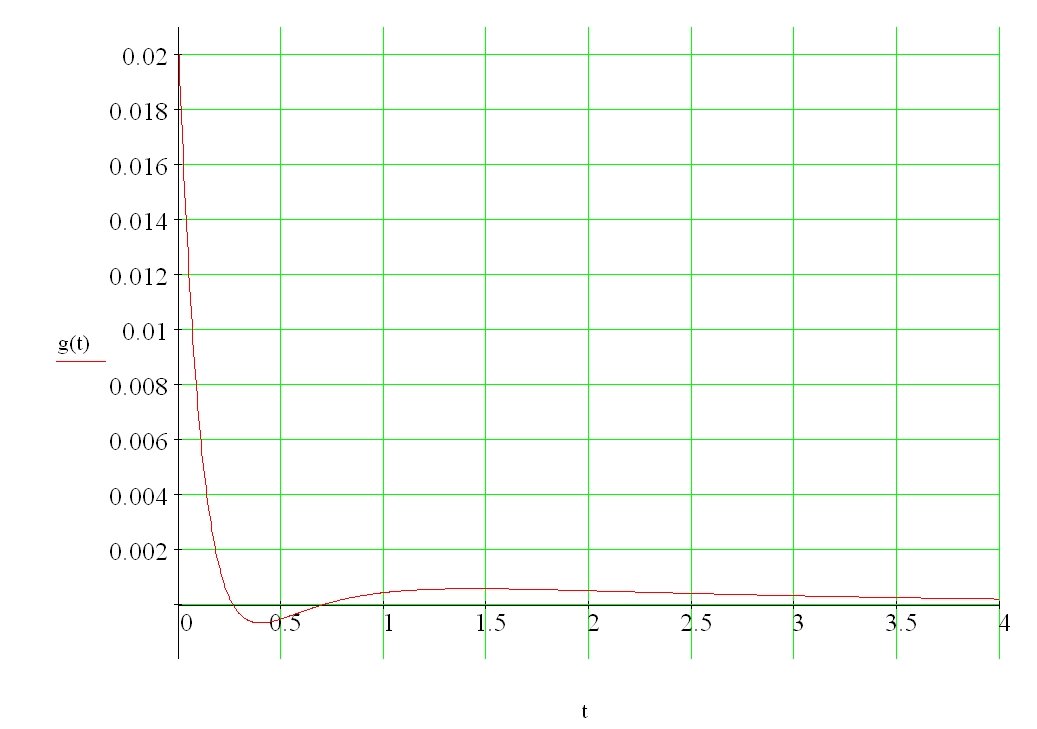
Рис. 4 График весовой функции
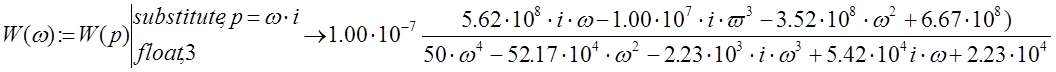
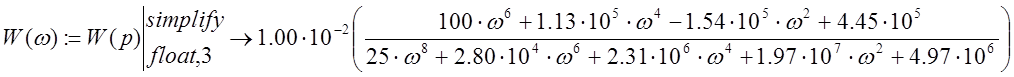
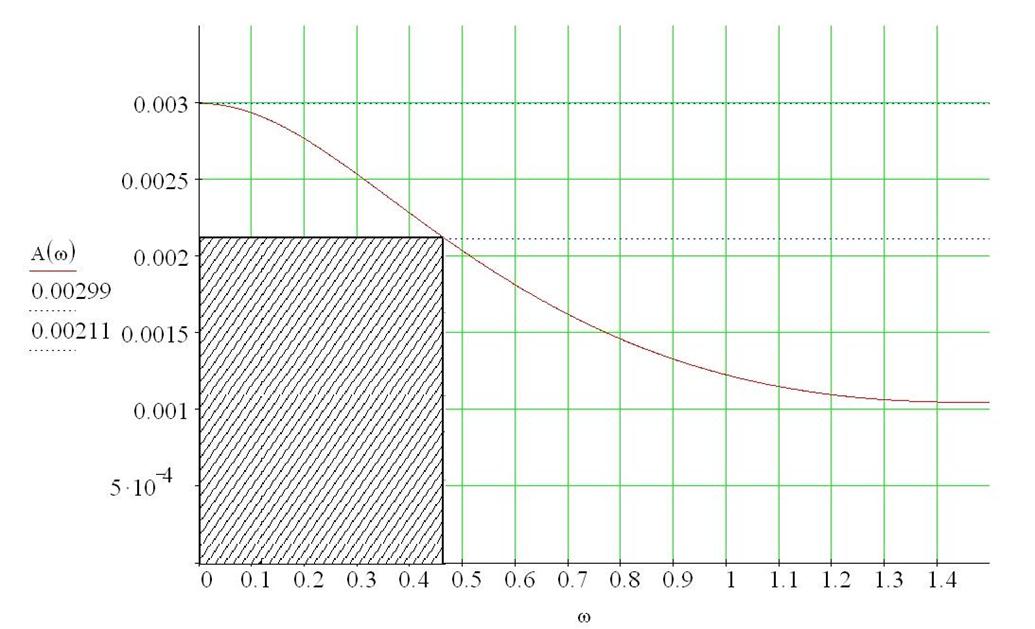
Рис. 5 График АЧХ
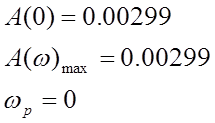
|
Частоту среза определить невозможно т.к. АЧХ не достигает единичного значения.
Для определения полосы
пропускания проведем 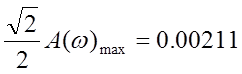
Полоса пропускания от ![]()
![]() до
до
![]()
Показатель
колебательности 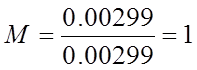
![]()
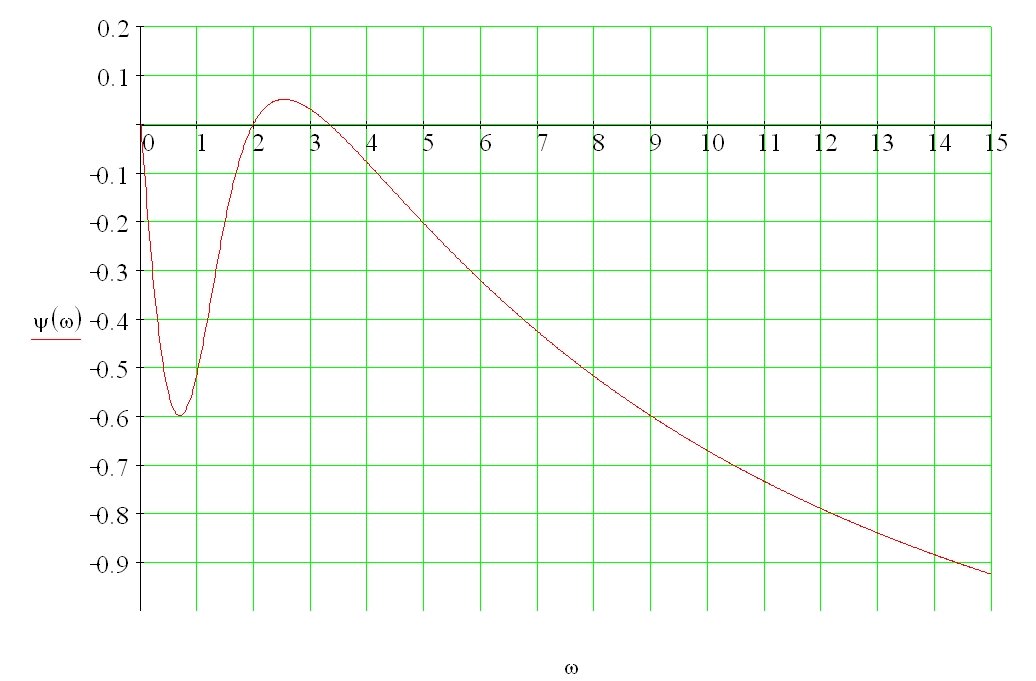 Рис. 6 График ФЧХ
Рис. 6 График ФЧХ
2. Синтез формирующего фильтра
Корреляционная функция:
![]()
![]()
Определим спектральную плотность случайного сигнала:
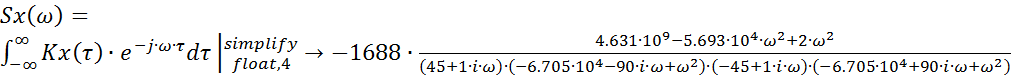
Построим график спектральной плотности:
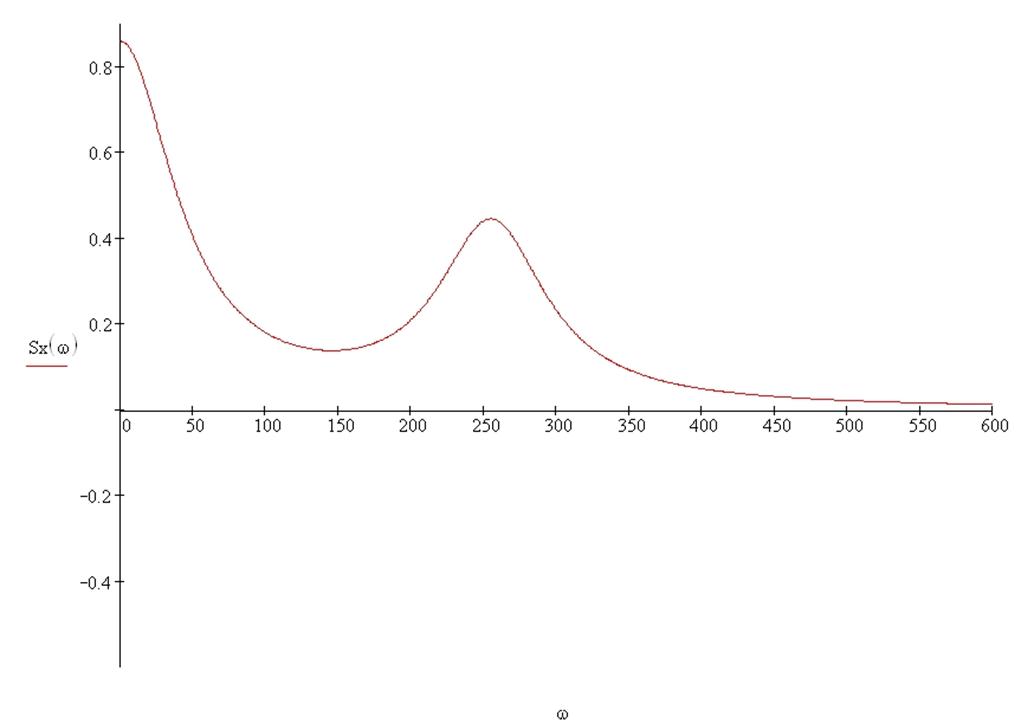
Рис. 7 График спектральной плотности
Передаточная функция формирующего фильтра ![]() находится из выражения:
находится из выражения:
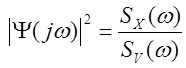
где ![]() - спектральная
плотность белого шума.
- спектральная
плотность белого шума.
Белый шум – стационарный случайный процесс, имеющий постоянную
спектральную плотность.
![]()
В рамках курсовой работы SV(ω) принимается равной 1.
Получаем для квадрата модуля частотной характеристики:
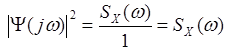
Находим корни знаменателя:
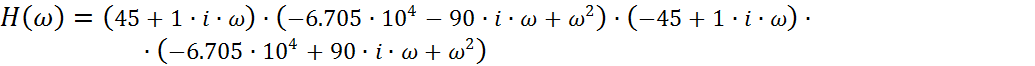
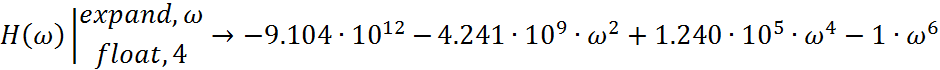
Из коэффициентов полинома составим вектор.
![]()
С помощью функции polyroots , в Mathcad, найдем корни знаменателя
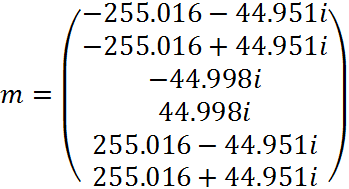
Строим корни на комплексной плоскости:
|
|
|
|
|
|
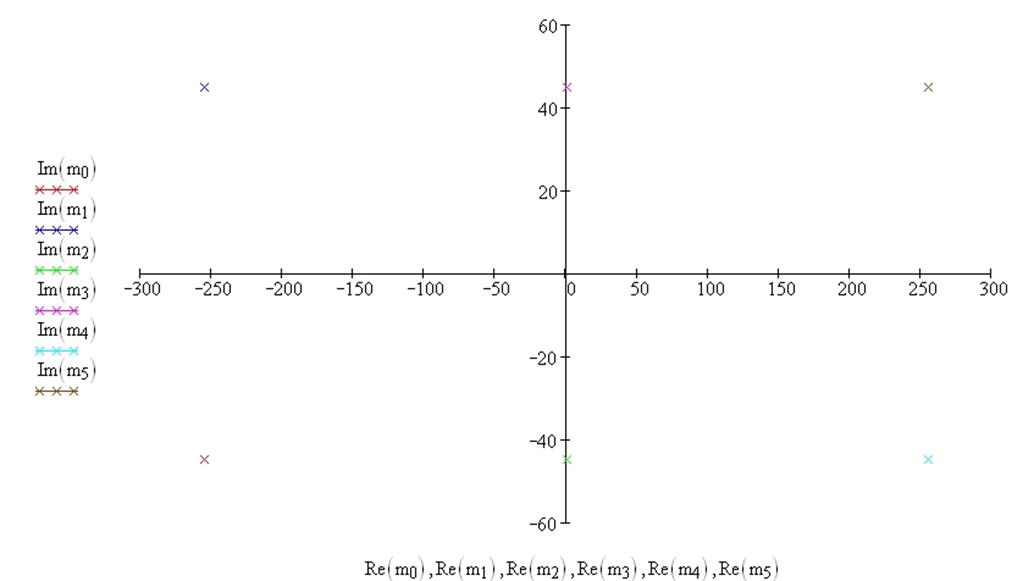
Рис. 8 График корней m на комплексной плоскости
Находим корни числителя:
![]()
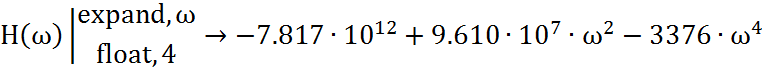
![]()
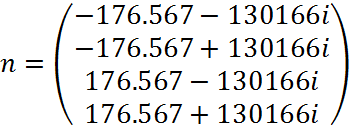
Строим корни на комплексной плоскости:
|
|
|
|
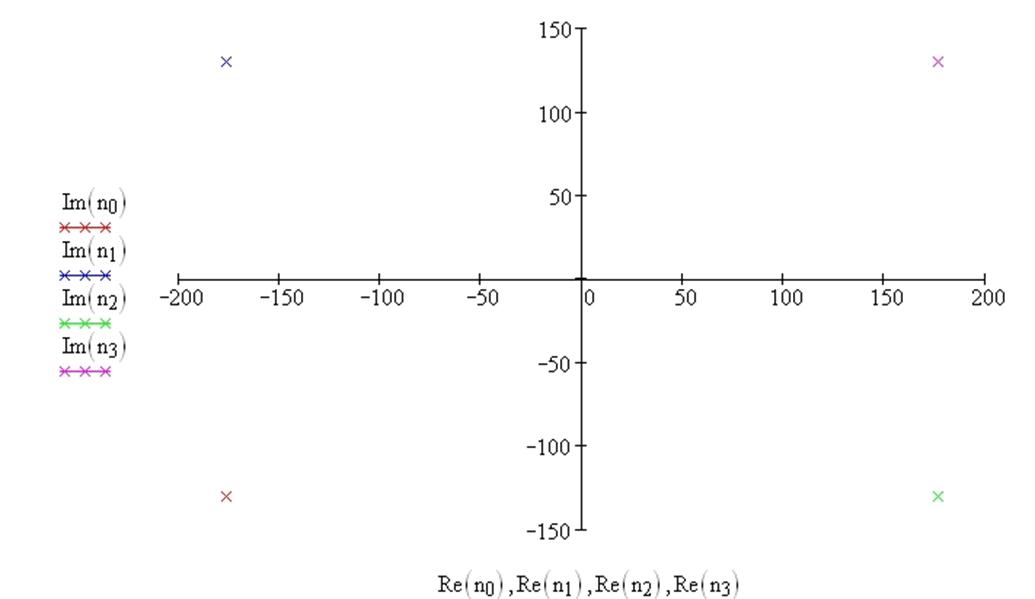
Рис. 9 График корней n на комплексной плоскости
Из корней верхней полуплоскости формируем выражение для :
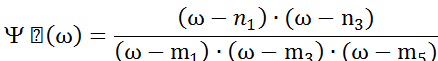
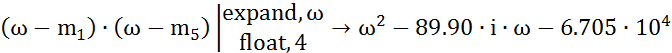
![]()
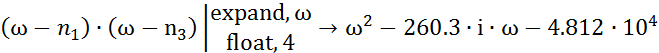
Так как сомножитель знаменателя![]() образуется
из решения уравнения
образуется
из решения уравнения
![]() то его можно заменить
непосредственно этим уравнением. Получаем:
то его можно заменить
непосредственно этим уравнением. Получаем:
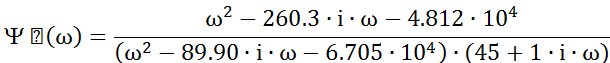
Преобразуем от iω к р:
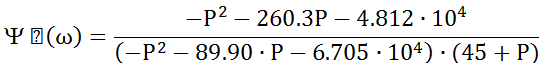
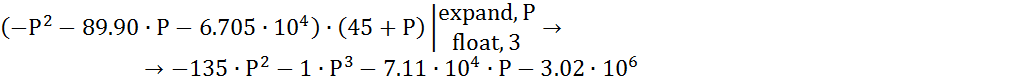
Приведя подобные получим передаточную функцию формирующего фильтра:
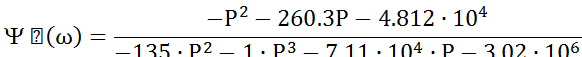
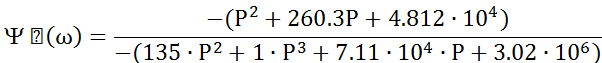
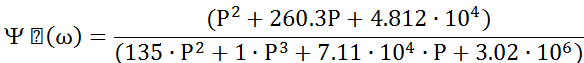
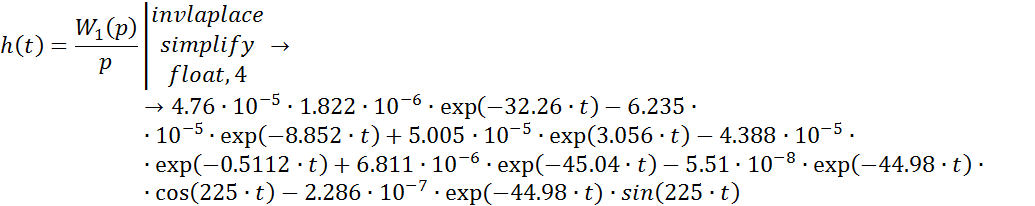
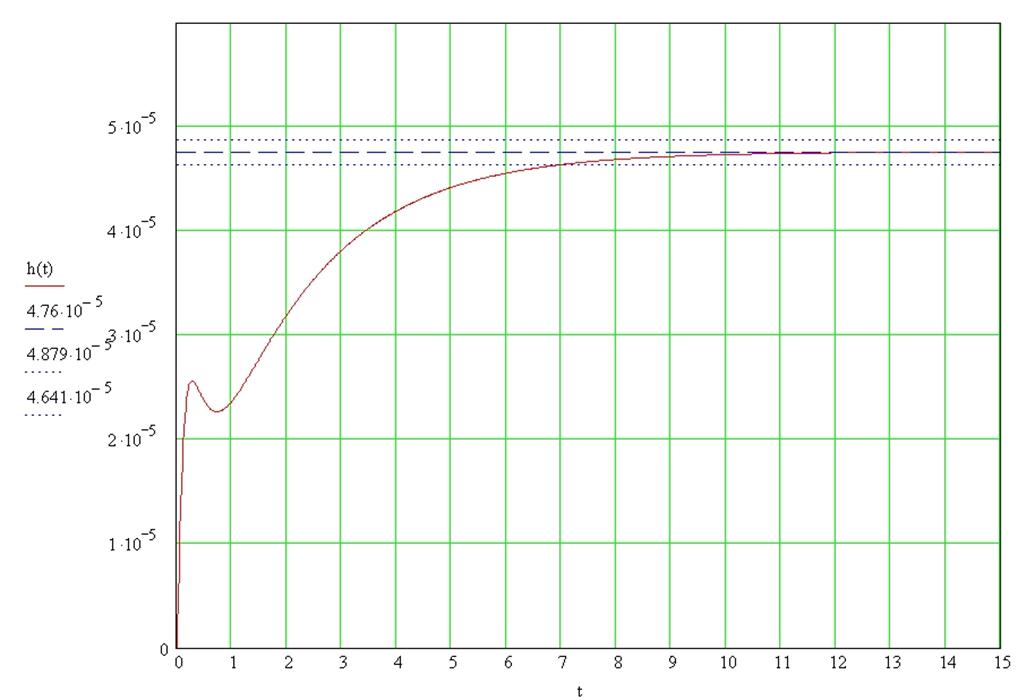 Рис. 10 График передаточной функции
Рис. 10 График передаточной функции
h(t)уст = ![]() –
установившееся значение переходного процесса
–
установившееся значение переходного процесса
h(t)max =![]() – максимальное значение
переходного процесса
– максимальное значение
переходного процесса
tпп= 7 с – Время переходного процесса
tсог= 12 с – Время первого согласования
tнар = 12 с – Время нарастания
n = 0 – Количество колебаний
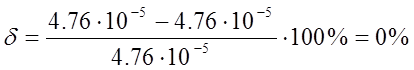 – Перерегулирование
– Перерегулирование
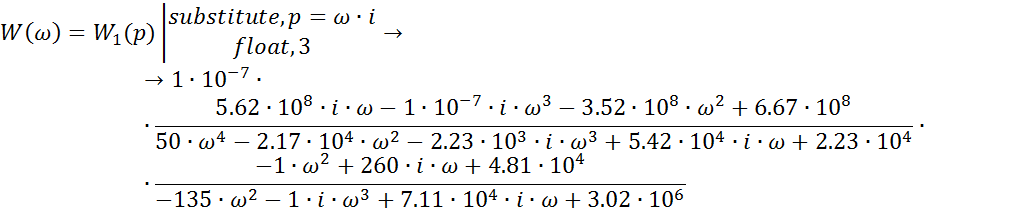
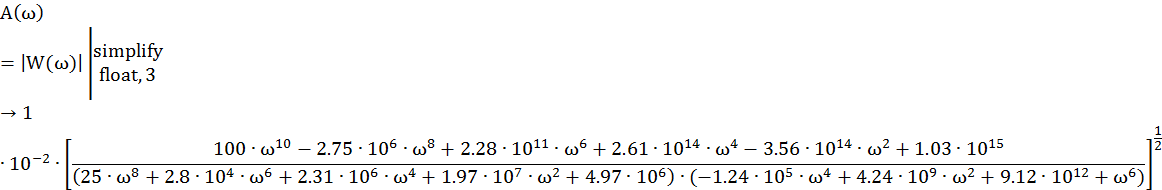
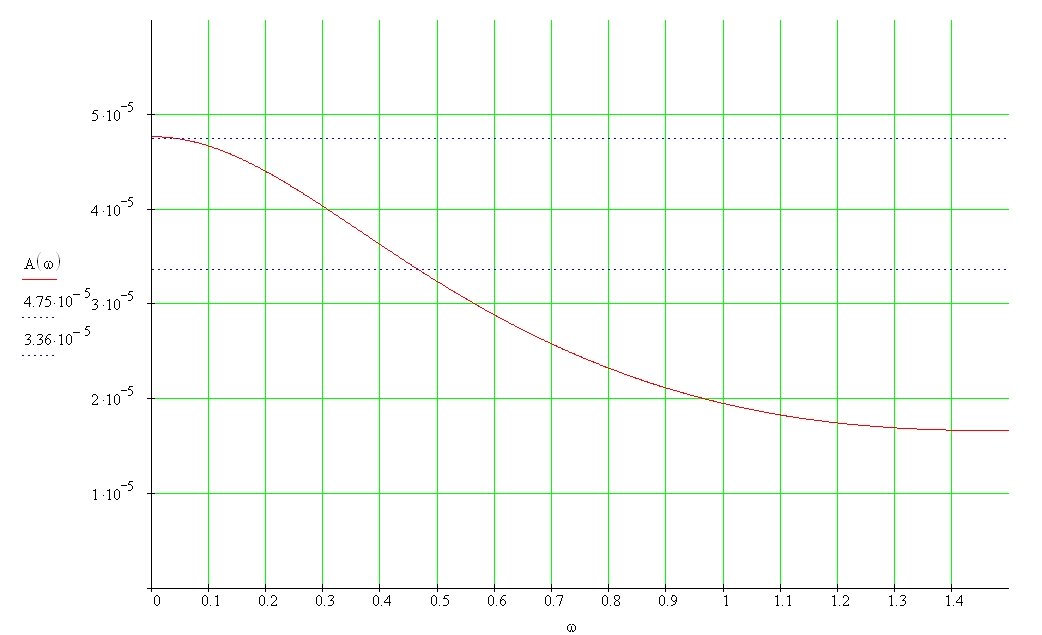
Рис. 11 График АЧХ
|
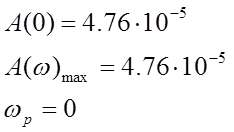
Частоту среза определить невозможно т.к. АЧХ не достигает единичного значения.
Для определения полосы
пропускания проведем 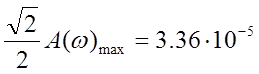
Полоса пропускания от ![]()
![]() до
до
![]()
Показатель
колебательности 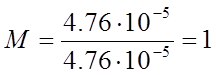
Вывод:
Анализируя полученные графики переходного процесса и АЧХ можно сказать, что формирующий фильтр, введённый в систему с объектом управления, не изменяет устойчивость этой системы. Изменились лишь некоторые показатели качества:
|
Без фильтра |
С фильтром |
|
hуст=0,00299 |
hуст=4.76*10-5 |
|
hmax=0,00299 |
hmax=4.76*10-5 |
|
A(0)=0.00299 |
А(0)=4.76*10-5 |
|
Amax=0.00299 |
Amax=4.76*10-5 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.