По графику АЧХ определим косвенные оценки качества ОУ:
Максимальное значение амплитуды:
Amax(ω)=0,5
Резонансная частота:
ωр=10 , Гц
Амплитуда сигнала при нулевой частоте
А(0)=0
Показатель колебательности:
М=Amax/A(0)=0
Полоса пропускания ![]()
6. СИНТЕЗ ФОРМИРУЮЩЕГО ФИЛЬТРА
По корреляционной функции KХ(τ) определим спектральную плотность SХ(ω) для белого шума (SV(ω)=const), который подается на вход формирующего фильтра.
Корреляционная функция задана выражением:
![]()
Найдем спектральную плотность случайного сигнала и построим ее график:
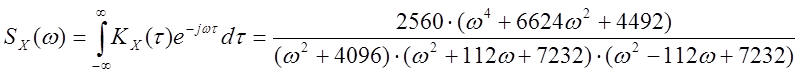
|
|
Рис. 9. Спектральная плотность
По заданным статическим характеристикам Sx и SV определим передаточную функцию формирующего фильтра Ψ(р), для чего воспользуемся уравнением:
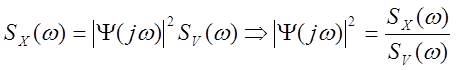
В рамках данной курсовой работы спектральная плотность SV(ω) принимается равной 1. Получаем, что квадрат модуля частотной характеристики определяется следующим образом:
![]()
Найдем корни числителя и
знаменателя ![]() .
.
Найдем корни числителя:
![]()
![]()
![]()
![]()
![]()
Определим корни знаменателя:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Строим корни на комплексной плоскости:
|
|
Рис. 10. Корни на комплексной плоскости
Из корней верхней полуплоскости формируем выражение для Ψ(jω):
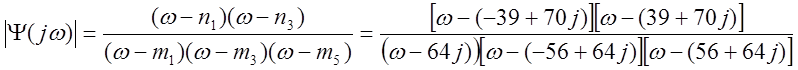
Так как сомножитель знаменателя ω-64j образуется из решения уравнения 64+jw, то его можно заменить непосредственно этим уравнением:
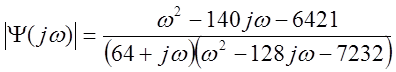
Запишем передаточную функцию формирующего фильтра, заменив jω на р:
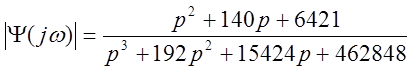
Представим ОУ в виде:
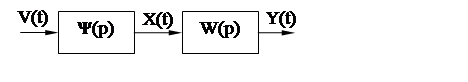
Рисунок 11. Эквивалентная схема с фильтром
Для этой системы определим общую передаточную функцию:
![]()
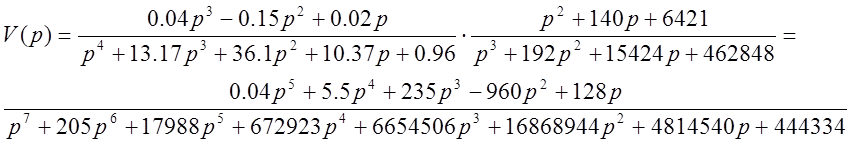
Определим устойчивость полученной системы по критерию Раусса для эквивалентной схемы.
Характеристическое уравнение имеет вид:
![]()
Вычисляем третью строку таблицы Раусса:
R3 = a0/a1=1/205=0,00488
C31 = a2 – R3a3=17988 – 0,00488·672923= 14704,13576
C32 = a4 – R3a5=6654506 – 0,00488·16868944=6572185,55328
C33 = a6 – R3a7=4814540 – 0,00488·444344= 4812371,60128
Вычисляем четвёртую строку таблицы Раусса:
R4 = a1/С31=205/14704,13576=0,01394
C41 = a3 – R4C32=672923– 0,01394·6572185,55328= 581306,73339
C42 = a5 – R4C33=16868944– 0,01394·4812371,60128= 16801859,53988
C43 = a7 – R4C34=0
Вычисляем пятую строку таблицы Раусса:
R5 = С31/С41=14704,13576/581306,73339=0,025
C51 = С32 – R5C42=6572185,56– 0,025·16801859,54= 6152139,15
C52 = С33 – R5C43=4812371,60128
Вычисляем шестую строку таблицы Раусса:
R6 = С41/С51== 581306,73339/6152139,15=0,09449
C61 = С42 – R6C52=16801859,54– 0,09449·4812371,60128= 16347138,0074
Т.к. коэффициенты R3, R4, R5, R6 положительны, система устойчива по критерию Раусса.
7. ОЦЕНКА КАЧЕСТВА ЭКВИВАЛЕНТНОЙ СХЕМЫ
Определим временные характеристики системы. Найдем переходную функцию по формуле и построим ее график:
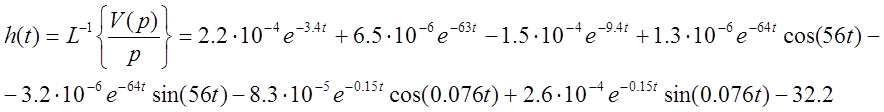
|
|
Рис. 12. Переходная функция скорректированной системы
По графику видно, что система является неустойчивой, поэтому прямые оценки качества провести в данном случае невозможно.
Определим частотные характеристики системы, вычислив амплитудно-частотную характеристику:
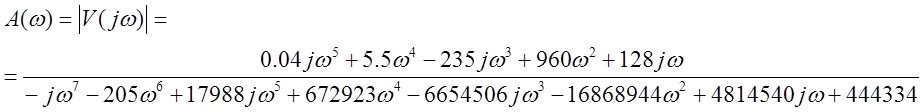
|
|
Рис. 13 Амплитудо-частотная характеристика скорректированной системы
По графику АЧХ определим косвенные оценки качества.
Максимальная амплитуда выходной величины Аmax=6,1∙10-5
Значение амплитуды при нулевой частоте А(0)=0
Резонансная частота ωр=1 Гц
Показатель колебательности 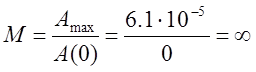 Данный результат возможен из-за неустойчивости
рассматриваемой системы.
Данный результат возможен из-за неустойчивости
рассматриваемой системы.
Полоса
пропускания ω1÷ω2 => 0,2÷8,8Гц (на графике 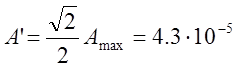 )
)
ВЫВОД
В первой части курсовой работы мы построили математическую модель системы в пространстве состояний, её структурную схему и сигнальный граф, вычислили её передаточную функцию по формуле Мейсона, определили временные и частотные характеристики, построили их графики и нашли прямые и косвенные оценки качества, при этом выяснили, что система является устойчивой.
Во второй части работы мы нашли передаточную функцию формирующего фильтра и перешли к эквивалентной схеме, добавив последовательно фильтр, для эквивалентной схемы построили графики переходной функции и АЧХ, по которым соответственно определили прямые и косвенные оценки качества. Также мы выяснили, что при подаче белого шума на вход формирующего фильтра, система остается неустойчивой. Сравним косвенные оценки качества исходной и скорректированной систем. Добавление формирующего фильтра привело к уменьшению максимально амплитуды АЧХ. Также по АЧХ эквивалентной схемы нельзя определить частоту среза, которая характеризует длину переходного процесса. Таким образом, добавление формирующего фильтра не улучшило качественные характеристики системы.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Ефремова Т.А., Власов В.В. Методические указания к выполнению практической работы «Построение математической модели объекта в пространственном состоянии и синтез формирующего фильтра»-Балаково,2008
2. Справочное пособие по теории систем автоматического регулирования и управления под ред. Е.А.Санковского – Минск: Высшая школа, 1973.
3. Брофеев Ю.И. Импульсная техника. -М.: Высшая школа, 1984.
4. Р.Ли Оптимальные оценки, определение характеристик и управление. -М.: Наука, 1966.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.