














1 ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОБЪЕКТА
УПРАВЛЕНИЯ В ПРОСТРАНСТВЕ СОСТОЯНИЙ
1.1 Построение математической модели для электрической схемы
Рассмотрим построение математической модели в пространстве состояний для объекта управления, представленного в виде электрической схемы, изображенной на рисунке 1.
|
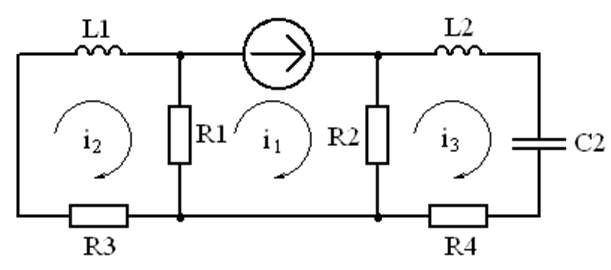
Рисунок 1 - Эквивалентная схема объекта управления
|
№ варианта |
Параметры элементов эквивалентной схемы объекта управления |
Выходная переменная |
|||||||||
|
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
L1, Гн |
L2, Гн |
L3, Гн |
С1, мкФ |
С2, мкФ |
||
|
10 |
328 |
395 |
118 |
215 |
- |
24 |
24 |
- |
- |
19605 |
i1 |
Таблица 1 - Параметры элементов схемы объекта управления
Вычисления производятся в системе MathCAD.
|
|
|
|
В третьем уравнении есть интеграл, поэтому дифференцируем его:
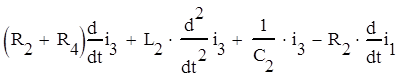 = 0 (4)
= 0 (4)
В уравнениях 1, 2 и 4 введем фиктивные переменные Х1, Х2 и Х3, но с производными на один порядок ниже:
![]() =
=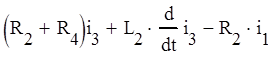 (5)
(5)
![]() =
= ![]() (6)
(6)
![]() =
= ![]() (7)
(7)
Находим производные от фиктивных переменных. Из (4) следует:
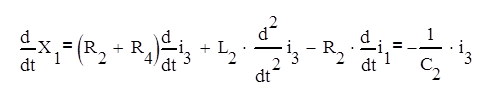 (8)
(8)
Из (5) следует:
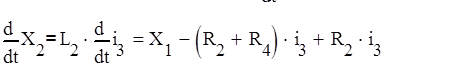 (9)
(9)
Из (2) следует:
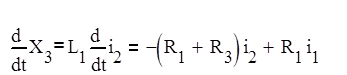 (10)
(10)
В данных уравнениях имеется 6 переменных: i1, i2, i3, X1, X2, X3. Необходимо уйти от i1, i2, i3, выразив их через X1, X2, X3.
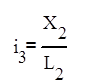 (6*)
(6*)
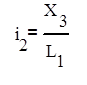 (7*)
(7*)
Подставляем в (1) выражения для токов (6*), (7*) и выражаем i1:
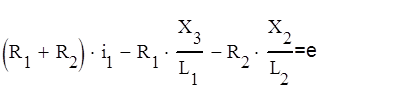
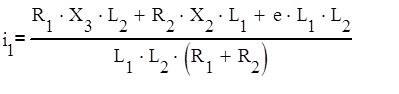
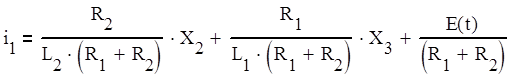 (11)
(11)
Выражаем через X1, X2, X3 их производные. Из (8) следует:
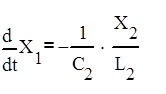 (12)
(12)
Подставляем значения токов в (9) и (10):
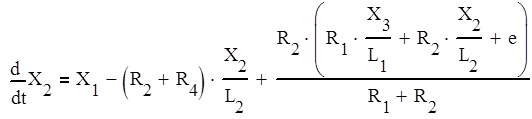
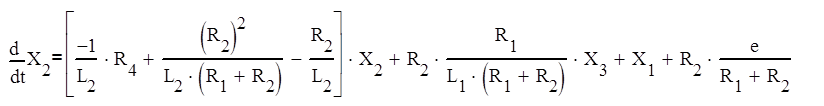 (13)
(13)
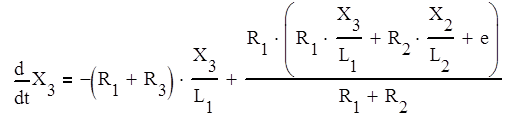
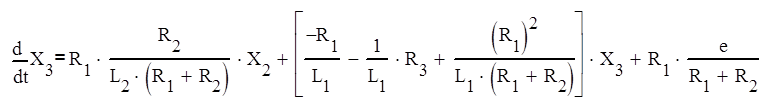 (14)
(14)
Теперь имеем уравнения, выраженные в зависимости от X1, X2, X3 и е(t). Запишем математическую модель данной системы в нормальной форме Коши:
![]() (15)
(15)
Уравнение (15) – это уравнение наблюдения для входной величины, где входное напряжение U равно ЭДС
U = |e|
Уравнение выходной величины объекта:
![]() (16)
(16)
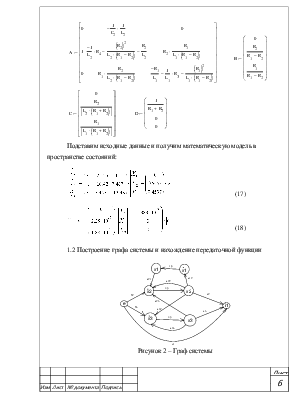
Основываясь на уравнениях (11), (12), (13) и (14), получаем запись уравнения Коши в матричной форме.
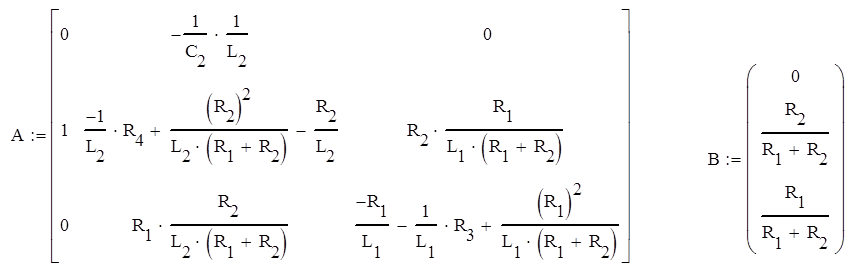
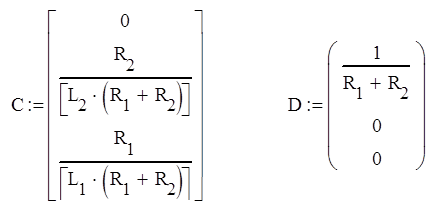
Подставим исходные данные и получим математическую модель в пространстве состояний:
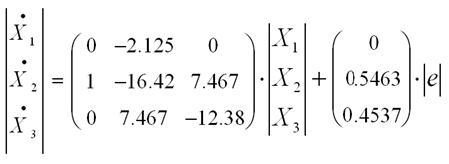 (17)
(17)
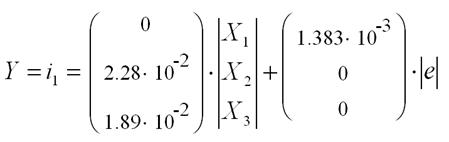 (18)
(18)
1.2 Построение графа системы и нахождение передаточной функции
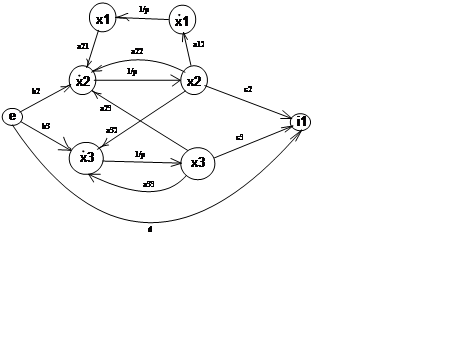
Рисунок 2 – Граф системы
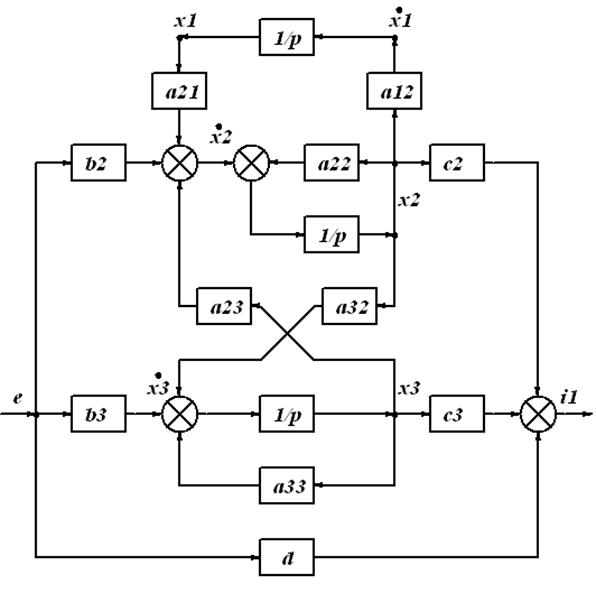
Рисунок 3 – Структурная схема системы
1.3 Нахождение передаточной функции схемы с использованием формулы
Мейсона
Формула Мейсона имеет вид:
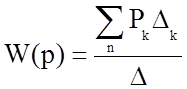 (19)
(19)
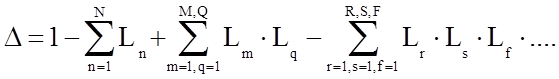 ,
,
где k - количество возможных прямых путей от входа к выходу;
∆ - определитель графа;
Рk - коэффициент передачи k-ого пути от входа к выходу;
∆к - определитель всех касающихся контуров при удалении k-ого пути;
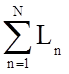 - сумма коэффициентов передачи всех
отдельных контуров;
- сумма коэффициентов передачи всех
отдельных контуров;
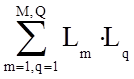 -сумма всех возможных
произведений из 2-ух не касающихся
-сумма всех возможных
произведений из 2-ух не касающихся
контуров;
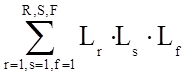 - сумма всех возможных комбинаций
из 3-ех не касающихся
- сумма всех возможных комбинаций
из 3-ех не касающихся
контуров.
Определим и запишем уравнения всех путей графа от входа к выходу:
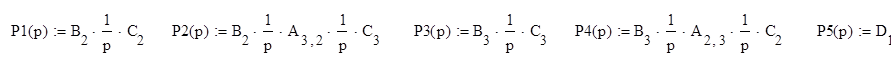
Найдем уравнения замкнутых контуров:
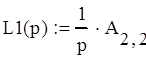
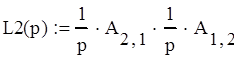
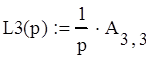
Запишем выражение для определителя графа:
![]()
Определители путей:
![]()
![]()
![]()
![]()
![]()
Передаточная функция графа и всей системы:
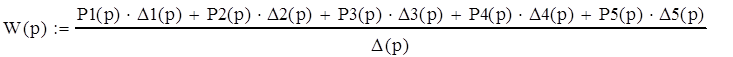
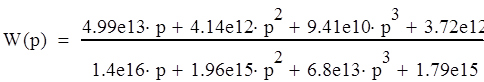 (20)
(20)
2 ПРЯМЫЕ И КОСВЕННЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМЫ
УПРАВЛЕНИЯ
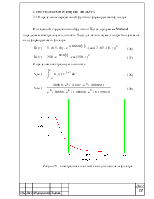
С помощью обратного преобразования Лапласа найдем переходную функцию по уравнению передаточной функции (20):
 (21)
(21)
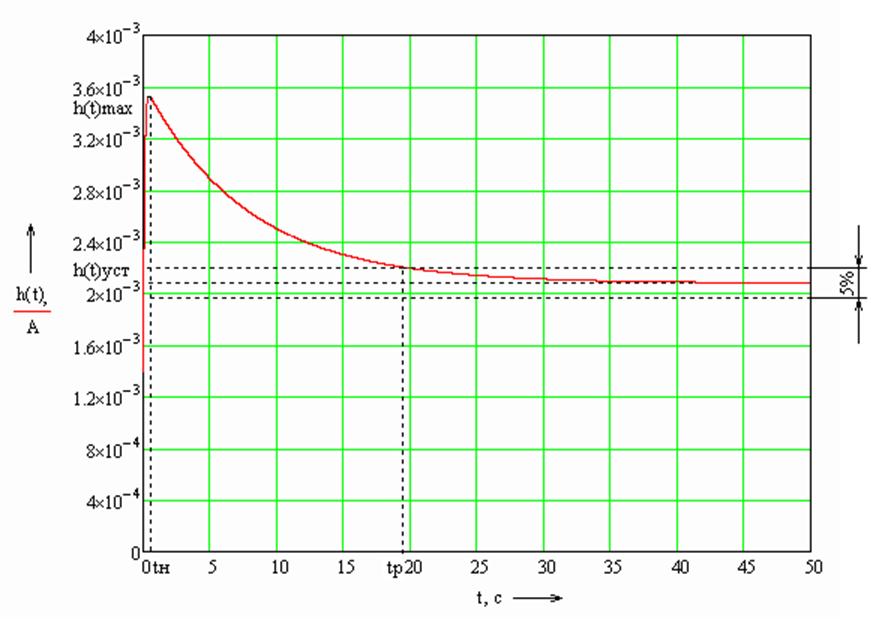
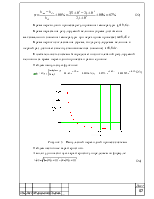
Рисунок 4 – Переходный процесс системы
Определим прямые оценки качества. Установившееся значение тока hуст равно 2,1∙10-3 А. Тогда 5% интервал отклонения от установившегося значения будет соответствовать следующей величине:
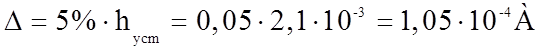
Величина перерегулирования выходного параметра при переходном процессе:
hmax = 3,5∙10-3 А
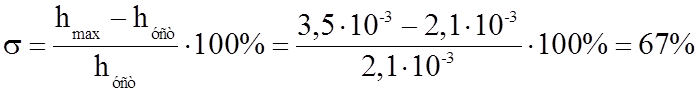 (22)
(22)
Время переходного процесса регулирования температуры tп=19,6 с.
Время нарастания регулируемой величины (время достижения максимального значения температуры при переходном процессе) tн=0,45 c.
Время первого согласования (время, когда регулируемая величина в первый раз достигает своего установившегося значения) t1=0,04 c.
Колебательность системы n определяет число колебаний регулируемой величины за время переходного процесса и равно единице.
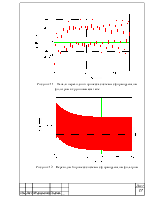
Найдем импульсную функцию:
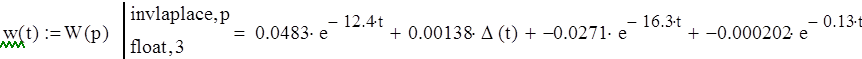 (23)
(23)
Рисунок 5 – Импульсный переходный процесс системы
Найдем частотные характеристики.
Амплитудно-частотную характеристику определяем по формуле:
![]() (24)
(24)
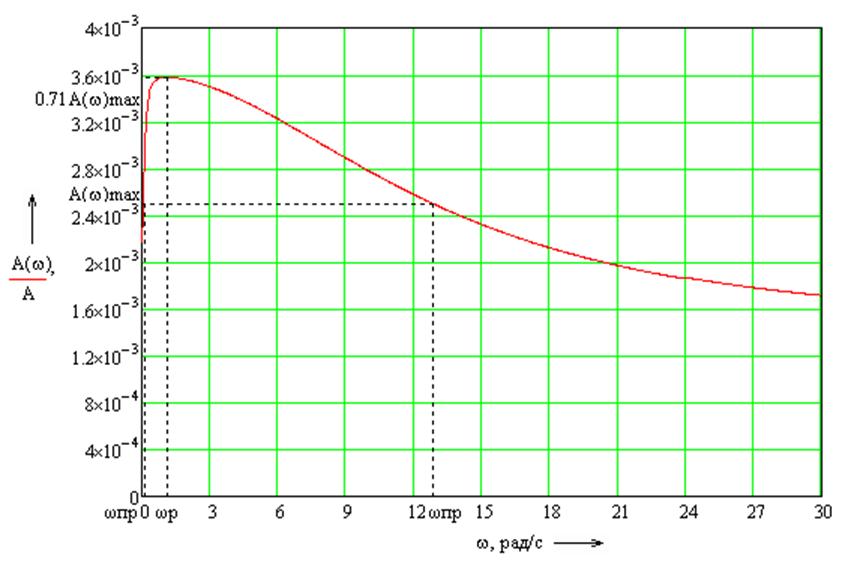
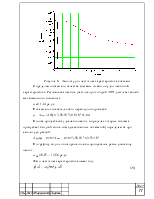
Рисунок 6 – Амплитудно-частотная характеристика системы
Определим показатели качества системы по амплитудно-частотной характеристике. Резонансная частота (частота при которой АЧХ достигает своего максимального значения):
ωр = 1,14 рад/с
Показатель колебательности переходного процесса:
μ = Аmax / A(0) = 3,58∙10-3/2,18∙10-3=1,64
Полоса пропускания (диапазон частот, в пределах которых система пропускает входной сигнал без существенных искажений) определяется при амплитуде, равной:
A(ωпр) = 0,707∙Amax = 0,707∙3,58∙10-3 = 2,53∙10-3
По графику видно, что ширина полосы пропускания равна диапазону частот:
ωпр = 0,07… 12,56 рад/с
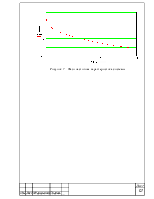
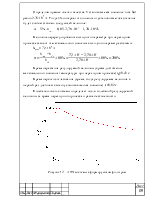
Фазо-частотная характеристика имеет вид:
![]() (25)
(25)
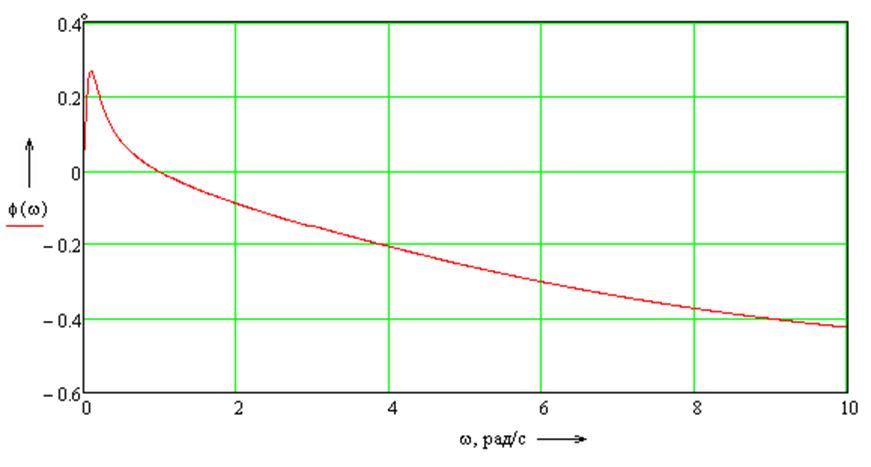
Рисунок 7 – Фазо-частотная характеристика системы
3 СИНТЕЗ ФОРМИРУЮЩЕГО ФИЛЬТРА
3.1 Определение передаточной функции формирующего фильтра
По заданной корреляционной функции Kx(τ) в программе Mathcad определяем спектральную плотность Sx(ω) для белого шума, который подается на вход формирующего фильтра.
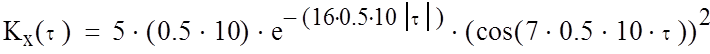 (26)
(26)
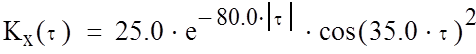 (27)
(27)
Определим спектральную плотность:
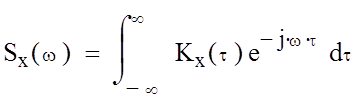 (28)
(28)
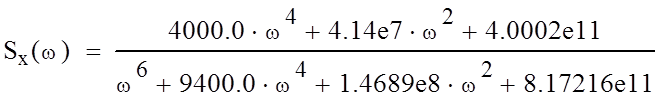 (29)
(29)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.