1. Построим математическую модель объекта управления в пространстве состояний.
Эквивалентная электрическая схема объекта управления приведена на рис.1
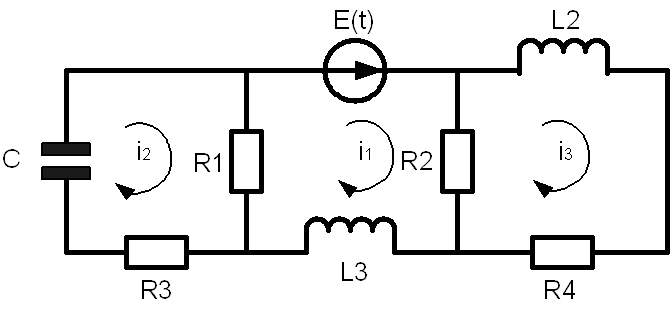
R1=343Ом
R2=378Ом
R3=119Ом
R4=233Ом
L2=23Гн
L3=47Гн
C1=43668*![]() Ф
Ф
Входной сигнал: U
Выходной сигнал: I3
1.Структурная схема объекта управления
В схеме 3 элемента, запасающих энергию, следовательно, ММ должна быть 3-го порядка.
При построении математической модели следует учитывать следующие выражения для связи токов, напряжений и комплексных сопротивлений элементов электрической схемы:
Для
сопротивления R U=R I=![]()
![]()
![]()
Для
индуктивности L U=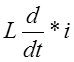 I=
I=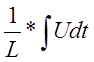 Z
Z![]()
![]()
Для емкости C U=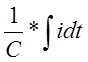 I=
I=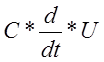 Z
Z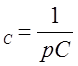
2.Построим математическую модель.
2.1. Зададимся направлением контурных токов I1, I2, I3.
2.2. Составим 3 уравнения по 2-му закону Кирхгофа для контуров.
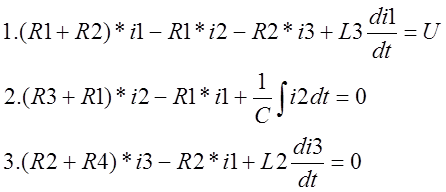
|
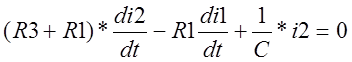
2.3.Введем вектор состояния объекта управления х1, х2, х3
![]() отсюда
отсюда
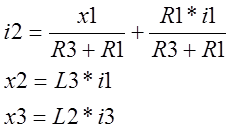
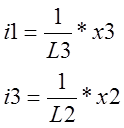
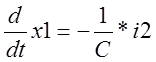
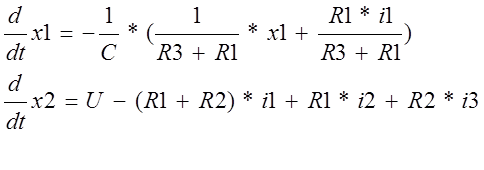
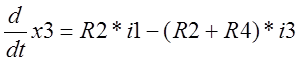
Подставим токи
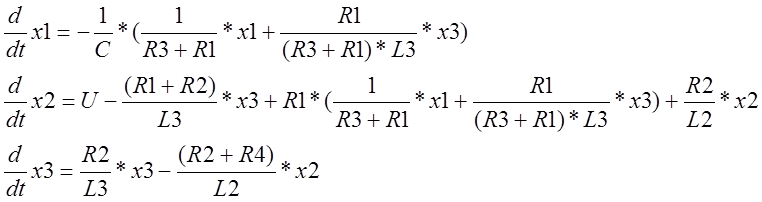
Упростим полученные выражения
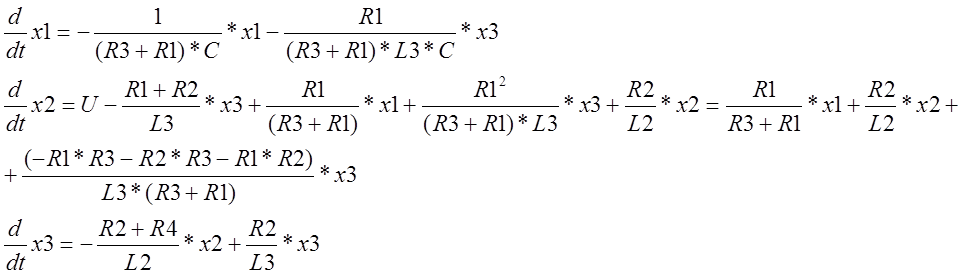
Запишем полученную систему дифференциальных уравнений в матричном виде.
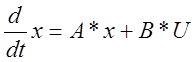
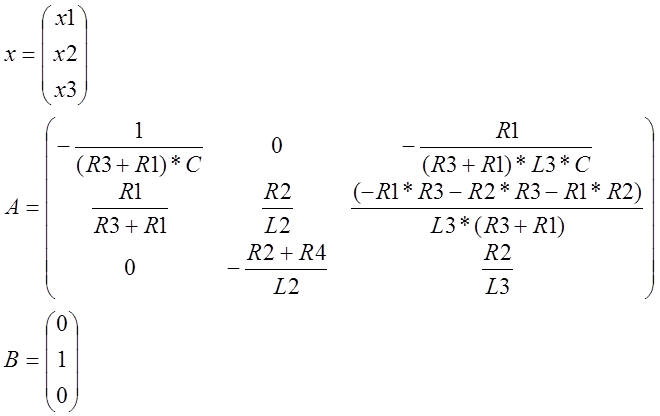
Получим матричное уравнение для выходной переменной
Y=C*x+D*U
Т.к. 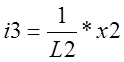 то
то 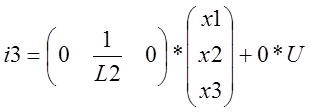
Тогда. С=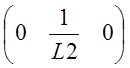
D=0
3.Построим граф системы, и по полученному графу найдем передаточную функцию системы.
Перепишем уравнение в общем виде для построения графа
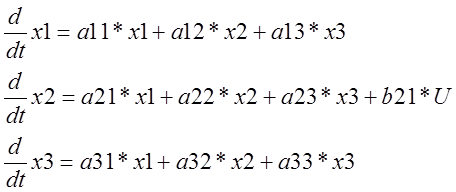 .
.
Построение графа производим за два шага.
1. Ставим точки входа, выхода системы U, I3 и векторы параметров x1, x2, x3.
2. Соединим все параметры связями согласно системе уравнений.
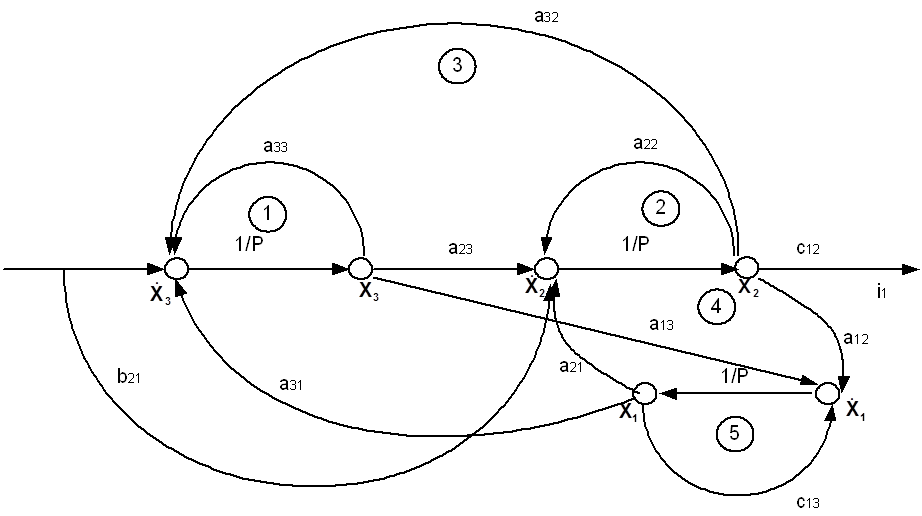
3.Составим структурную схему ОУ
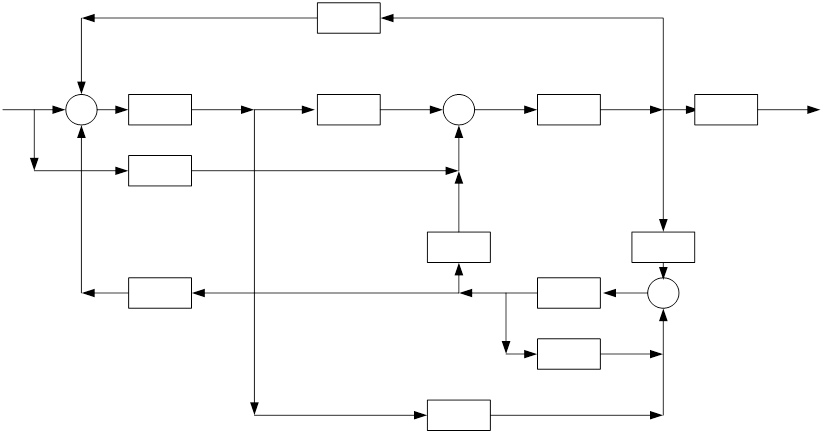
Найдем передаточную функцию системы по формуле Мейсона.
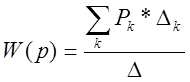
к - количество возможных путей от входа к выходу
![]() -определитель графа
-определитель графа
![]() - коэффициент передачи к пути
от входа к выходу
- коэффициент передачи к пути
от входа к выходу
![]() -определитель всех касающихся
контуров при удалении к - го пути
-определитель всех касающихся
контуров при удалении к - го пути
1.В данном случае имеется один путь от входа к выходу
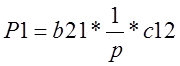
2.В системе имеется 5 замкнутых контура:
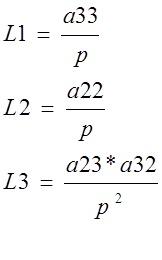
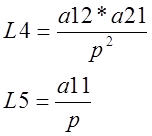
3.Определитель системы включает 5 контуров и 4 пары не касающихся контуров
![]()
4.![]()
5.Запишем и преобразуем выражение передаточной функции:
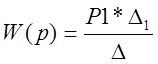
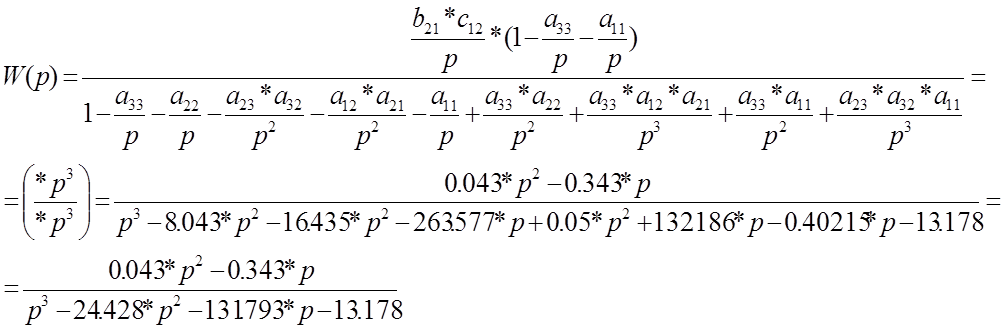
4. По полученной передаточной функции найдем выражение для весовой и переходной характеристик и построим их графики.
Найдем корни характеристического уравнения
![]()
p1=-4.81
p2=-0.106
p3=29.015
1.весовую характеристику системы найдем по формуле
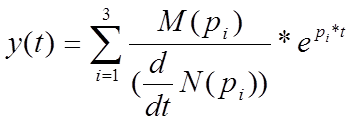
Рассчитаем компоненты весовой функции
M (p) =p*(0.043*p-0.343)
M (p1) =2.385
M (p2) =0.035
M (p3) =26.216
N (p) =![]()
N1 (p) =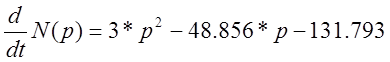
N1 (p1) =59.674+217.897-131.793=145.778
N1 (p2) =0.031+4.983-131.793=-126.779
N1 (p3) =2523-1416.824-131.793=974.383
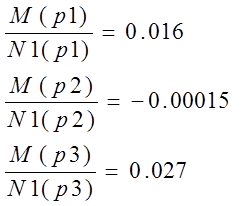
Весовая характеристика будет иметь вид
w (t)=![]()
2.Найдем переходную характеристику системы
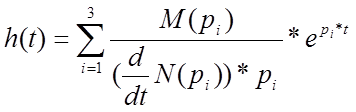
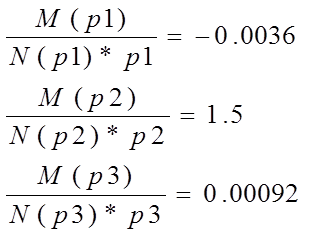
Переходная характеристика системы будет иметь вид
![]()
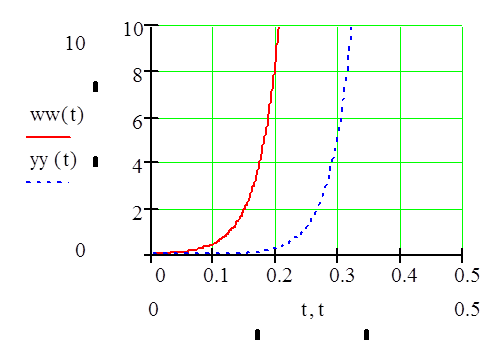
Построим графики весовой и переходной функции
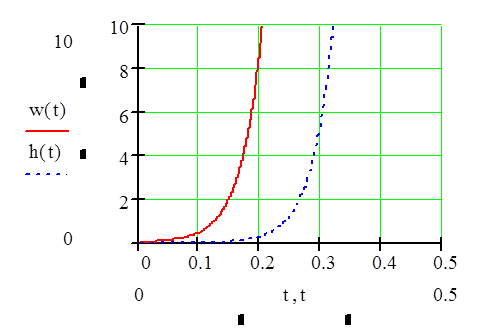
Построение весовой и переходной характеристик системы, используя преобразования MathCAD.
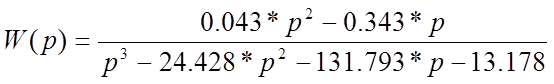
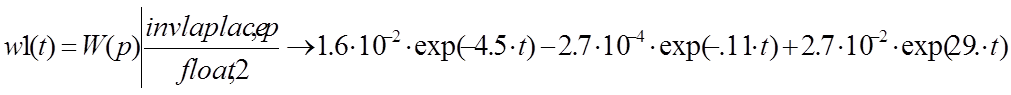
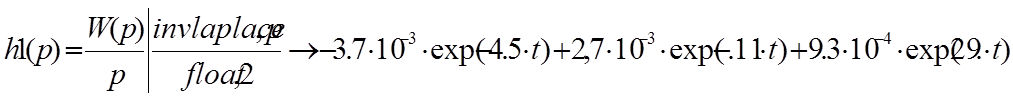
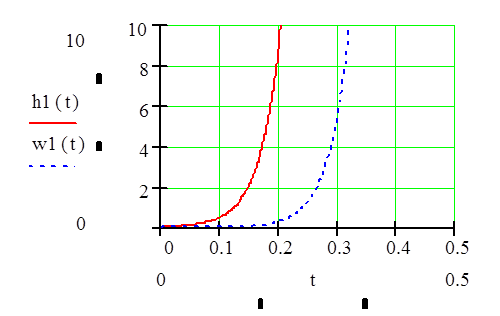
Данное решение совпадает с решением, полученным в ручную
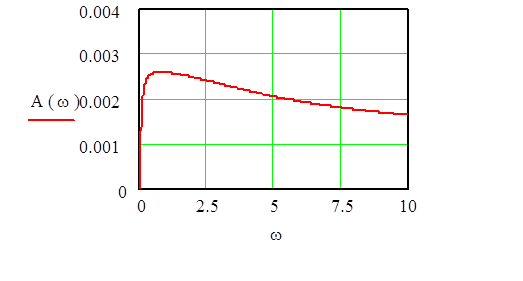
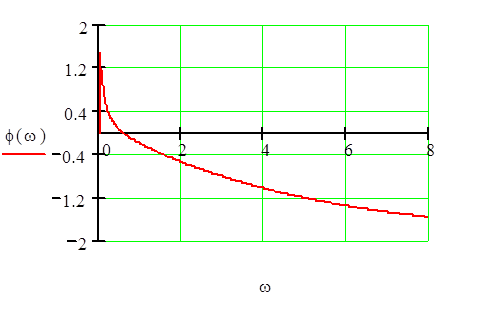
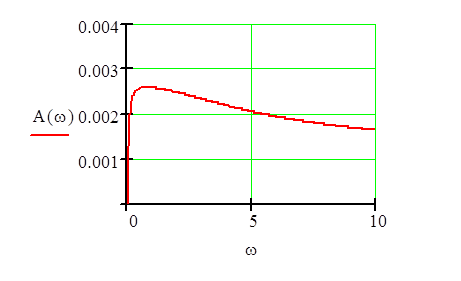
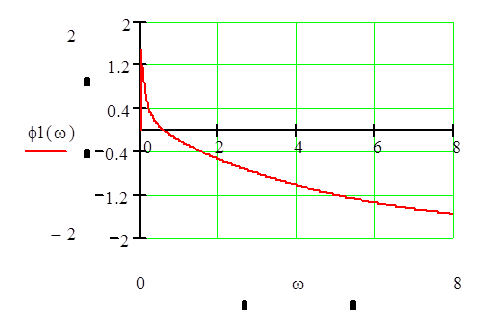
5.Расчитаем и построим графики амплитудно–частотной и амплитудно–фазовой характеристик, логарифмических частотных характеристик элемента системы управления.
Ручной расчет по передаточной функции.
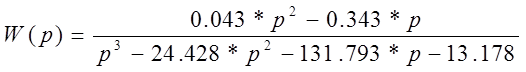
для этого сделаем замену в передаточной функции p=j*w
W (jw) =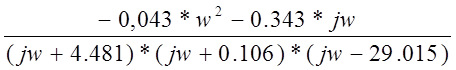
Освободимся от мнимых чисел в знаменателе путем умножения числителя и знаменателя выражения на комплексно сопряженное число знаменателю.
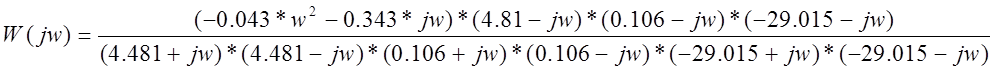
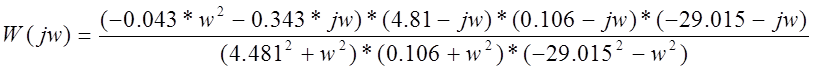
После перемножения скобок приведения подобных членов и разделения вещественной и мнимой частей в числителе получаем.
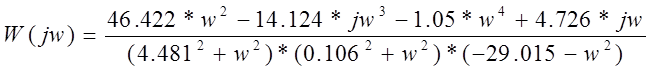
U (w) =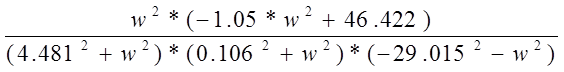
V (w) =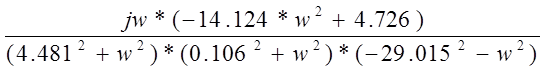
A (w) =![]()
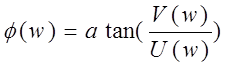
Операторный метод расчета.
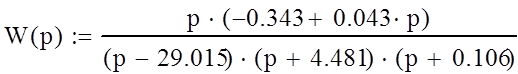
Заменим p=jw
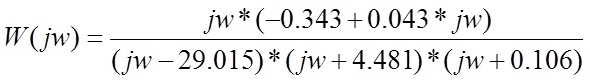
j=![]()
U (w) =Re (W (j*w))-вещественная частотная характеристика
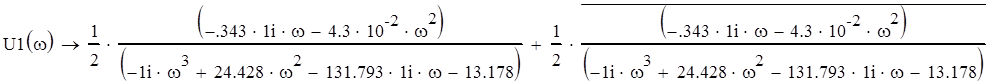
![]() -мнимая частотная
характеристика
-мнимая частотная
характеристика
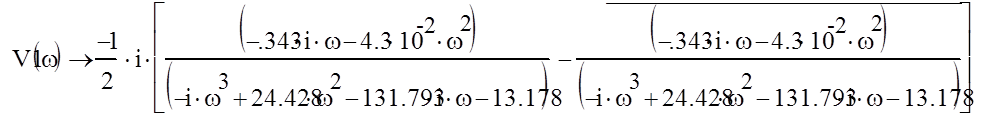
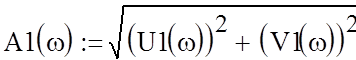 -амплитудно-частотная
характеристика
-амплитудно-частотная
характеристика
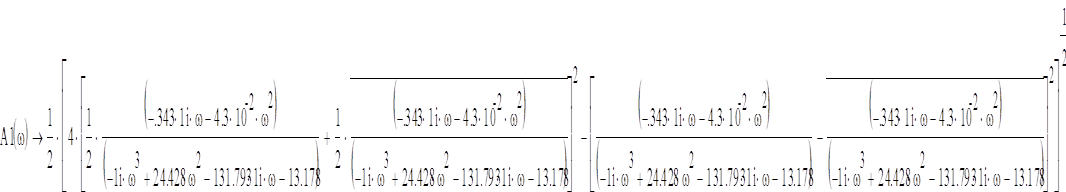
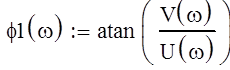
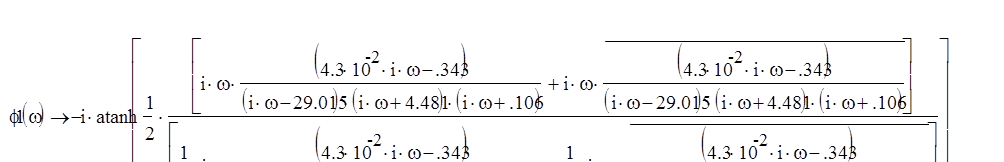
6. Решение уравнения Коши при ступенчатом и импульсном входе.
Решение уравнения Коши имеет вид
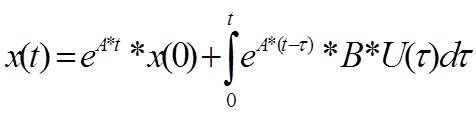
При нулевых начальных условиях первый член равен 0
Нахождение матричной переходной функции производим по формуле Лагранжа-Сильвестра.
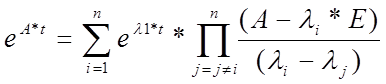
Введем параметры матрицы А, B, C.
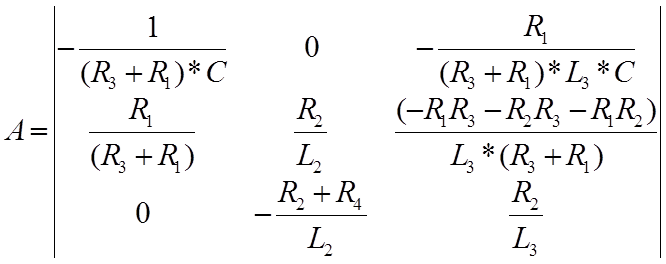
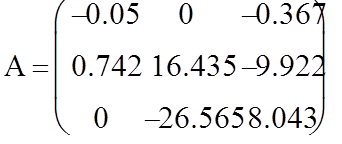
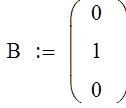
![]()
Найдем корни матрицы А
![]()
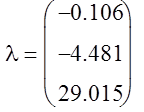
Единичная матрица Е
![]()
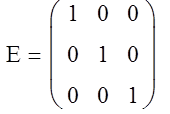
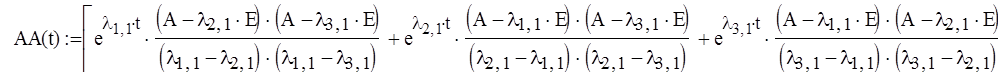
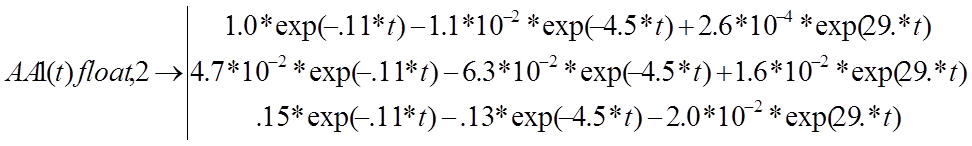
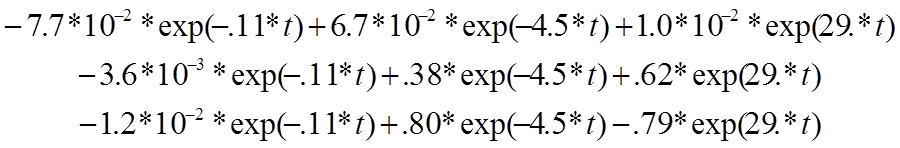
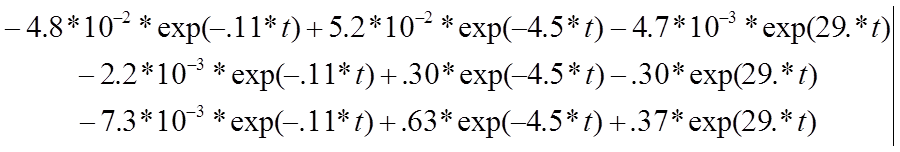
В данном случае матрица В не зависит от времени и U(t)=1. Подынтегральное выражение
Равно:
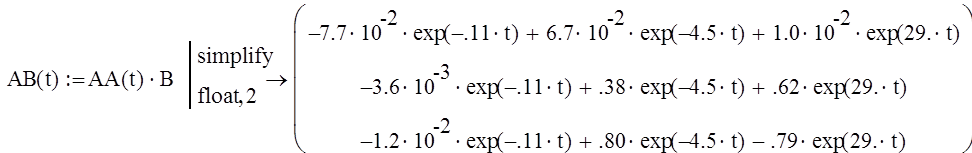
Матрицы в MathCAD не интегрируются и не дифференцируются. Поэтому надо интегрировать отдельно элементы матриц. Нам необходимо найти выражение для
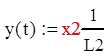
поэтому далее используем только строку для
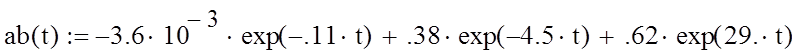
Интегрируем выражение решения уравнения Коши для переменной х2
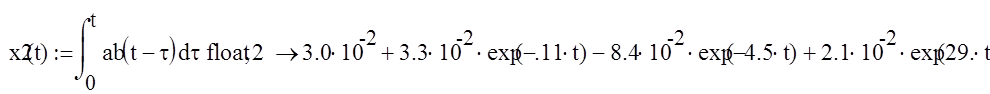
Переобозначим х2(t) в xx2(t)
![]()
Найдем выходную переменную через элементы матриц. С и D
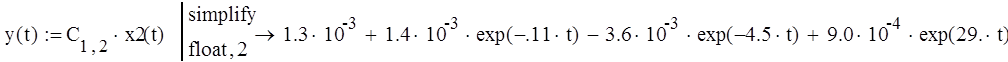
![]()
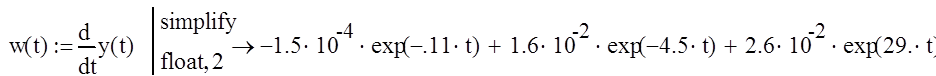
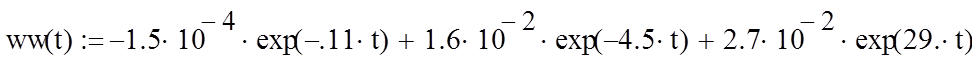
Решение совпадает с решением, полученным в ручную
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.