Понятие устойчивости нелинейных систем. Метод гармонического баланса (гармонической линеаризации, метод фильтра)

Устойчивость НСАР

I.  Понятие устойчивости нелинейных систем

Впервые теория устойчивости нелинейных систем разработанным русским учёным Ляпуновым.

Дадим определение устойчивости НСАР в смысле Ляпунова.

Ранее было показано, что каждой совокупности начальных условий соответствует определённая фазовая траектория системы, т.е. определённое её движение. Выберем из всех возможных движений НСАР какое-либо одно и назовём его невозмущённым. Выбор такого движения произволен и невозмущенным может быть любое движение. Тогда всякое другое движение, отличное от первого, будем называть возмущённым. То есть возмущённое и невозмущённое движение – это движение одной и той же НСАР (т.е. это одно и тоже дифференциальное уравнение, но при разных начальных условиях).

Обычно в качестве невозмущённого движения, устойчивость которого исследуется, выбирается движение (решение дифференциального уравнения), не зависящее от начальных условий (например, решение дифференциального уравнения, у которого правая часть равна нулю), соответствующее состоянию равновесия.

НСАР может иметь несколько таких состояний, как устойчивых, так и не устойчивых.

Тогда можно так определить устойчивость нелинейной САР: невозмущённое движение устойчиво, если при достаточно малых начальных возмущениях, вызванное ими возмущённое движение при  сколь угодно мало отличается от невозмущённого.

Невозмущенное движение асимптотически устойчиво, если при  возмущённое движение стремится к невозмущённому.

Устойчивость НСАР и асимптотическая устойчивость объединяются понятием устойчивость по Ляпунову. Иногда говорят об устойчивости по Ляпунову и асимптотической устойчивости, т.е. эти понятия различают.

Устойчивая асимптотически НСАР всегда устойчива по Ляпунову, обратное не всегда верно.

Если же возмущённое движение не стремится к невозмущённому, нелинейная САР не устойчива.

Ляпуновым предложено два метода устойчивости НСАР:

-  первый метод Ляпунова применяется для систем с несущественной нелинейностью. Он основан на линеаризации нелинейности разложением в ряд Тейлора в окрестности некоторой точки и отбрасывании всех членов порядка выше первого.
Линейное уравнение, полученное таким образом, называется уравнением в вариациях (в приращениях) или уравнением первого приближения (если учитывать члены второго порядка, то имеем уравнение второго приближения).
Ляпунов доказал, что об устойчивости в малом НСАР можно судить по устойчивости линейной САР, описываемой уравнением первого приближения. То есть невозмущённое движение нелинейной системы асимптотически устойчиво, если асимптотически устойчива линейная САР, определяемая соответствующим уравнением первого приближения. Если же линейная САР находится на границе устойчивости, то об устойчивости НСАР ничего нельзя сказать и этот вопрос требует специальных исследований.
Таким образом, первый метод Ляпунова сводит НСАР с несущественными нелинейностями к линейным САР, описываемым уравнениями первого приближения, для которых применим весь аппарат линейной теории управления.

-  Второй методЛяпунова даёт достаточные условия устойчивости, т.е. граница устойчивости определяется с запасом. Величина этого запаса неизвестна и может быть сколь угодно большой.
Введём понятие функции Ляпунова. Рассмотрим некоторую функцию координат фазового пространства V (в случае фазовой плоскости V является функцией X и Y, т.е. ).
Функция называется знакопостоянной, если она имеет один и тот же знак повсюду, кроме некоторых точек, в которых она равна нулю.
Функция называется знакопеременной, если при всех значениях переменных она имеет один и тот же знак, а в начале координат равна нулю.
Определённо-положительная функция всегда (за исключением начала координат) больше нуля, определённо-отрицательная – всегда меньше нуля.
Функции Ляпунова находятся с помощью дифференциального уравнения системы и представляет семейство замкнутых поверхностей в фазовом пространстве системы, уравнения которых (в частном случае фазовой плоскости) имеют вид:

При С стремящемся к нулю поверхность стягивается в точку и V = 0.

Очевидно, что если НСАР устойчива, изображающая точка стремится к состоянию равновесия – началу координат (Рис.1)

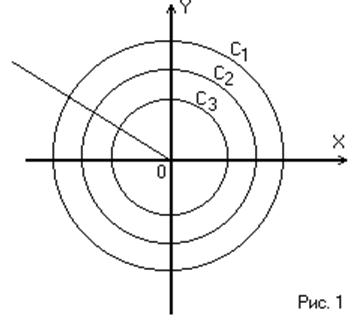
При этом по мере движения изображающей точки по фазовой траектории функция V убывает (как видно из Рис. 1, определённо-положительная функция убывает и, следовательно, её производная по времени отрицательна).

Таким образом, соотношение знаков функции V и её производной по времени являются критерием устойчивости НСАР. При этом, если НСАР асимптотически устойчива, изображающая точка стремится к нулю, и, следовательно, производная функции V есть знакоопределённая функция. Если же НСАР имеет неасимптотическую устойчивость, точка равновесия находится в некоторой области вблизи от начала координат, и, следовательно,  знакопостоянная функция.

Таким образом, условия устойчивости по Ляпунову можно сформулировать так:

·  если существует знакоопределённая функция V, производная которой по времени представляет собой знакопостоянную функцию противоположного с V знака, то невозмущённое движение устойчиво.

·  Если же  является знакоопределённой функцией противоположного с V знаком, то невозмущённое движение устойчиво асимптотически.

Функции, удовлетворяющие этим требованиям, и называются функциями Ляпунова, а их нахождение и является сутью второго метода Ляпунова. Задача нахождения функций Ляпунова чрезвычайно сложна и общего рецепта на все случаи НСАР пока ещё не найдено. Функции Ляпунова найдены для небольшого класса систем. Этой же задачей, кроме Ляпунова, занимались Лурье, Постников и др. Им удалось найти функции V для некоторых нелинейностей.

II.  Метод гармонического баланса (гармонической линеаризации, метод фильтра)

Идея метода заключается в линеаризации нелинейностей, при этом коэффициенты линеаризации зависят от амплитуды входного сигнала, т.е. нелинейность заменяется «пучком» линейностей, наклон которых зависит от величины входного сигнала. Этот метод достаточно точен и может быть применён как к несущественным, так и к существенным нелинейностям (метод Крылова-Боголюбова).

Идея метода основана на том, что линейные части многих систем имеют хорошие фильтрующие свойства, т.е. являются фильтром низких частот. Такой характеристикой обладают инерционные и интегрирующие звенья, АЧХ которых изображены на рис. 2 из которых и состоит линейная часть

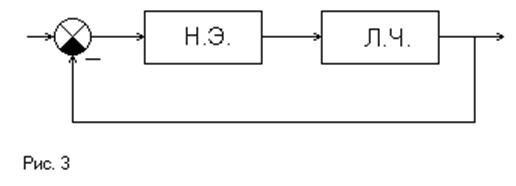
Если разложить выходной сигнал нелинейной части (рис.3) в ряд Фурье, можно считать, что линейная часть пропускает только первую гармонику разложения и отфильтровывает остальные, и, следовательно, на выходе линейной части остаётся гармонический сигнал. Таким образом, метод гармонического баланса также представляет собой метод линеаризации, при котором нелинейный сигнал на входе линейной части (а значит и на выходе нелинейной части) заменяется линейным сигналом – первой гармоникой разложения нелинейного сигнала. Обоснованность такой линеаризации тем выше, чем большими фильтрующими свойствами обладает линейная часть.

Итак, при гармонической линеаризации реальный нелинейный элемент (НЭ) заменяется идеальным, выходной сигнал которого равен первой гармонике разложения в ряд Фурье выходного сигнала реального НЭ.

Задача гармонической линеаризации состоит в том, чтобы определить эквивалентный комплексный коэффициент усиления НЭ (гармонический коэффициент передачи, описывающая функция), представляющий комплексный коэффициент передачи идеального НЭ, выходной сигнал которого представляет первую гармонику разложения в ряд Фурье выходного сигнала реального НЭ.