Понятие устойчивости нелинейных систем. Метод гармонического баланса (гармонической линеаризации, метод фильтра), страница 2

Будем считать, что на вход НЭ подаётся гармонический сигнал, являющийся выходом линейной части (Рис. 4)

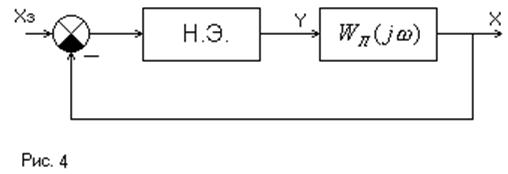Разложим выходной сигнал  Н.Э. в ряд Фурье и удержим только первую гармонику разложения (большинство нелинейностей  - нечётные).

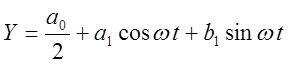
(т.к. функция нечётная, то , вторая, четвёртая и т.д. гармоники равны нулю)

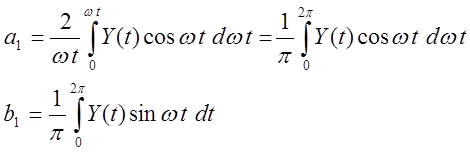
Поэтому:

 - комплексный коэффициент передачи нелинейного элемента

,

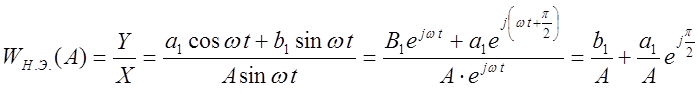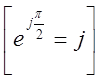
Тогда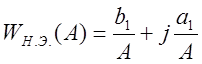

Обозначим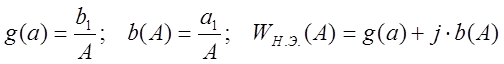      

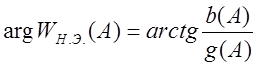
где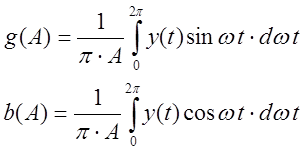

Замечания: В случае, если нелинейность кососимметричная и не содержит неоднозначности, первая гармоника выходного сигнала совпадает по фазе с входным сигналом, т.е. не содержит косинусоидальной составляющей, т.е. .

После линеаризации уравнение Н.Э. принимает вид:

Пример 1:

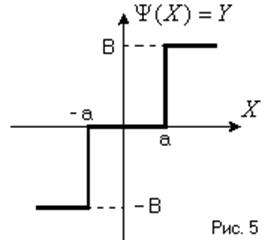
Найти , если нелинейность имеет вид (Рис. 5)

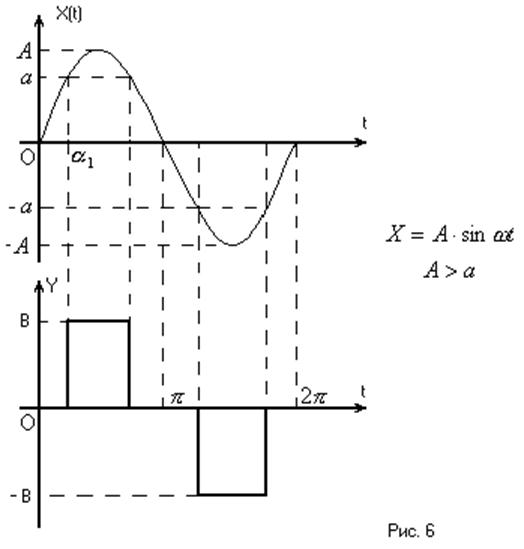
На вход нелинейного элемента поступает синусоидальный сигнал , тогда Y будет гармонической функцией вида (Рис. 6)

Нелинейность, как видно из рис. 6, кососимметрична относительно начала координат и не имеет зоны неоднозначности, следовательно , а уравнение нелинейного элемента будет иметь вид:

            (1)

при этом

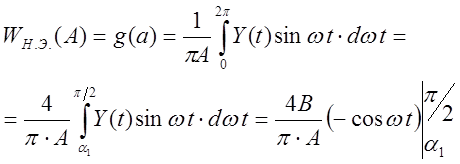
Из рис. 6 видно, что при ; , тогда , .

Следовательно,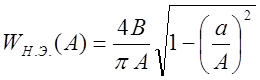

Удобно представить эквивалентный комплексный коэффициент усиления в функции безразмерной амплитуды входного сигнала 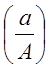, тогда

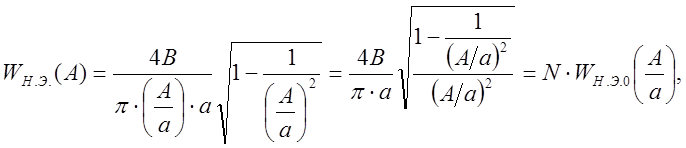
где

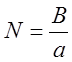 - нормирующий множитель, представляющий характеристику нелинейного элемента;

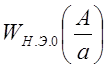 - нормированный эквивалентный комплексный коэффициент передачи Н.Э.

Достоинство такого представления в том, что 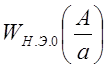 зависит только от одной переменной – безразмерной амплитуды, и его значения могут быть протабулированы.

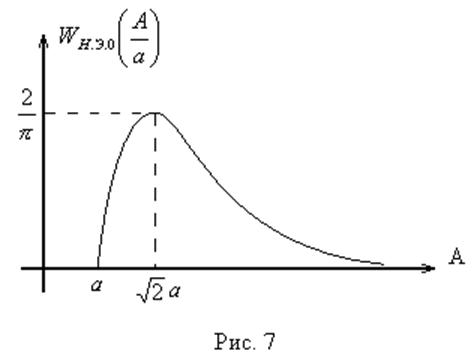
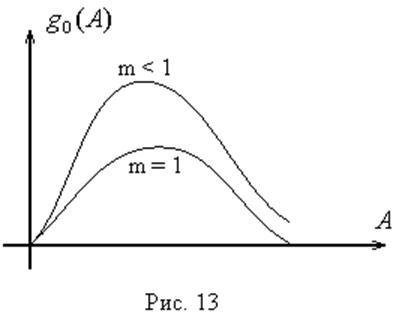
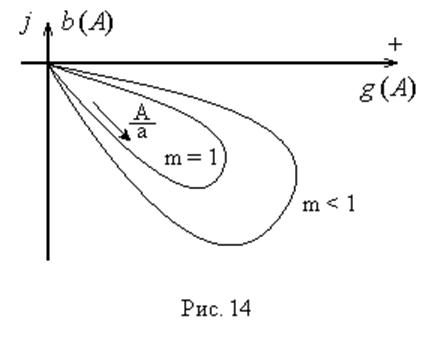
График 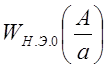 имеет вид (рис. 7)

При А < а выходной сигнал нелинейного элемента отсутствует (зона нечувствительности), следовательно .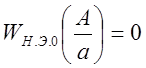

При  выходной сигнал нелинейного элемента равен B = const, следовательно, 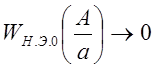, т.е. зависимость имеет экстремальный характер.

Найдём экстремум .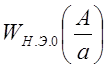
Обозначим:

 

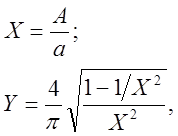
Тогда

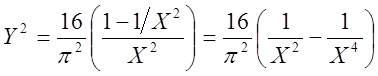
Найдём точку экстремума, т.е. значение X, при котором 

.

,

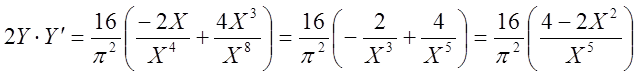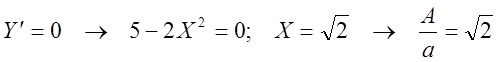т.е. при  имеем экстремум:

;

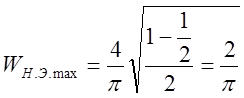Геометрическое место точек конца вектора  в комплексной плоскости  при изменении амплитуды входного сигнала А от 0 до  называется годографом эквивалентного комплексного коэффициента передачи или амплитудной характеристикой нелинейного элемента. Строится эта характеристика так же, как обычная АФЧХ, но только является функцией амплитуды. В данном примере  и амплитудная характеристика совпадает с осью (рис. 8).

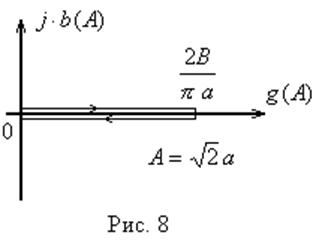
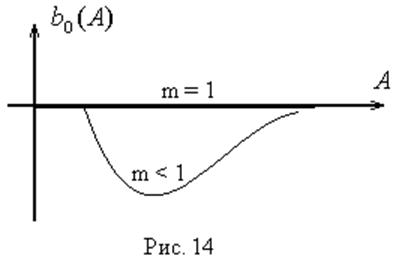
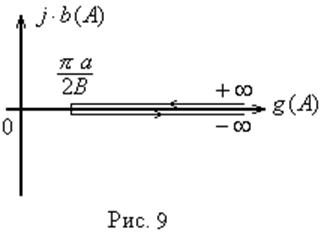
Обратной амплитудной характеристикой  нелинейного элемента называется вектор, обратный вектору :   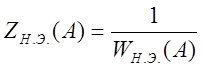            (рис. 9).

Пример 2:

                                    

;

                

III.     Исследование устойчивости НСАР методом гармонического баланса

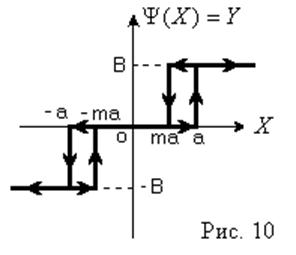
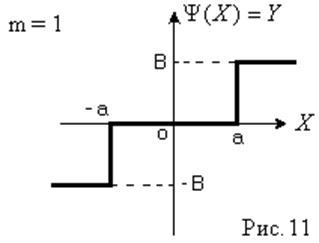
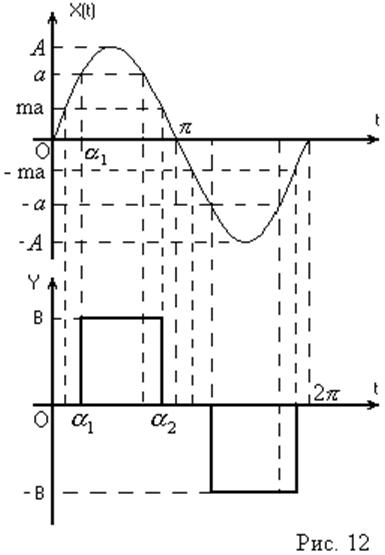
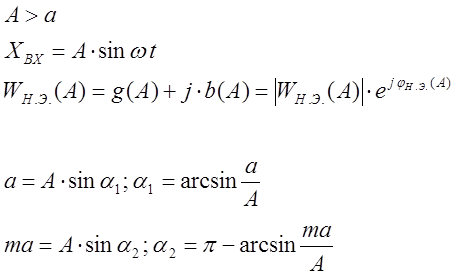
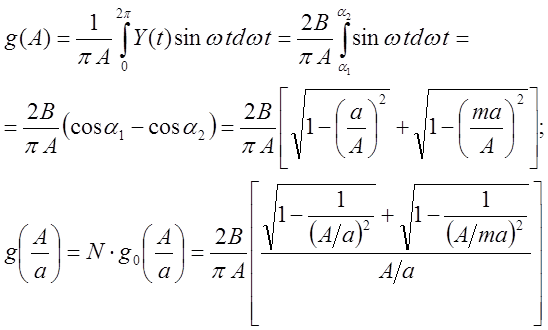
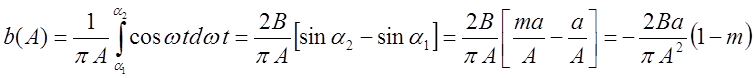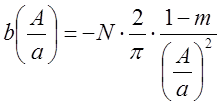
Метод гармонической линеаризации заключается в линеаризации НСАР разложением в ряд Фурье выходного сигнала нелинейного элемента и отбрасыванием всех гармоник разложения, кроме первой, т.к. линейная часть представляет фильтр низких частот.

К исследованию линеаризованной системы можно применить весь аппарат линейной теории управления, и, в частности, критерии устойчивости.

Непосредственное решение линеаризованного уравнения НСАР очень трудно или даже невозможно. Для этой цели разработаны графоаналитические методы. В зависимости от используемых критериев эти методы можно разделить следующим образом:

1.  Гольдфарб Л.С. (1946 г.) и Кохенбургер (1956; США) разработали графоаналитические методы на основе критерия Найквиста;

2.  Попов Е.П. разработал метод на основе критерия Михайлова;

3.  Магнус (ФРГ) – на основе критерия Гурвица.

Рассмотрим частотно-амплитудный метод Гольдфарба.

Структурная схема нелинейной САР приведена к виду (рис. 16)

Передаточная функция замкнутой системы запишется следующим образом:

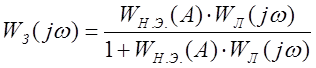         (1)

Характеристическое уравнение:

    (2)

Условие границы устойчивости по Найквисту:

    (3)

из уравнения (3):

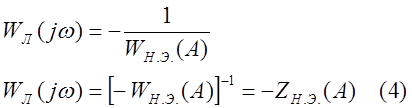
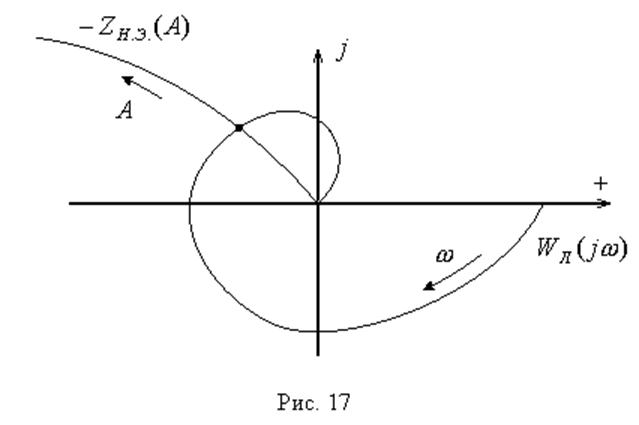Гольдфарб предложил решить это соотношение графически, строя отдельно АФЧХ  линейной части и обратную амплитудную характеристику  нелинейного элемента. Точки пересечения их и являются решением данного выражения (рис. 17).

Точкам пересечения  и  соответствуют автоколебания с частотой , определяемой по АФЧХ  линейной системы и амплитудой А, определяемой по характеристике .

Если же характеристики не пересекаются, следовательно, автоколебания отсутствуют, и САР устойчива. Вместо уравнения (4) можно воспользоваться уравнением 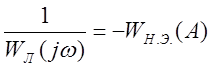                    (5)

т.е. строить характеристики  (инверсная АФЧХ линейной части) и . Этот метод был предложен Кохенбургером.

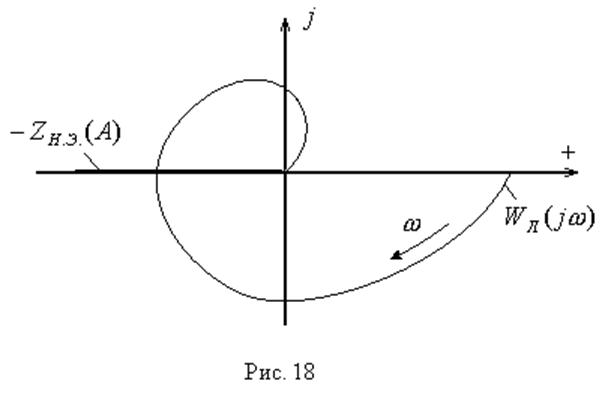В частном случае, когда характеристика нелинейного элемента однозначная , совпадает с осью абсцисс (рис. 18).

Поэтому характеристика  в точках пересечения с характеристикой  может принимать только действительные значения, т.е. частота колебаний находится из условия , а амплитуда – из уравнения .

Устойчивость автоколебаний

Характеристики  и  имеют вид:

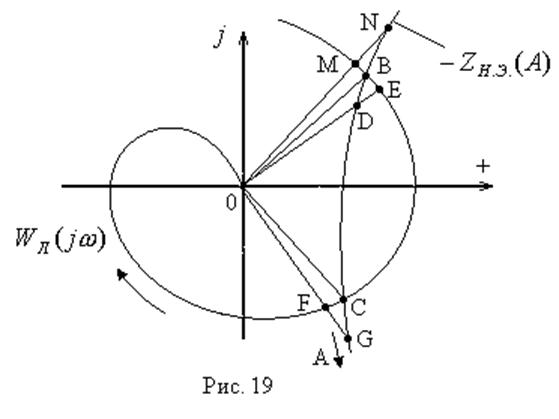
Исследуем устойчивость автоколебаний в точках В и С. В этих точках спрведливо равенство:

 или , т.е., согласно критерию Найквиста САР находится на границе устойчивости.

Пусть

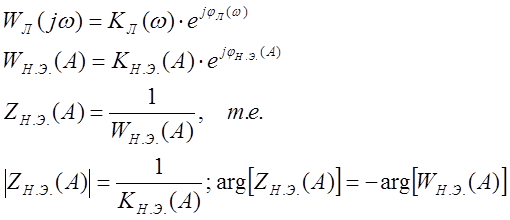
Тогда в точках В и С имеем:

,

т.е. 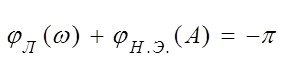        (6)

Рассмотрим точку В. Пусть амплитуда колебаний увеличилась на  (вектор OD). Определим вектор , соответствующий частоте, при которой вектор  пересекает ось абсцисс, т.е. вектор для которого .

Фаза вектора   уменьшалась по сравнению с вектором   на , следовательно фаза вектора  увеличилась на . Для того, чтобы фаза вектора  равнялась , фаза вектора  также должна уменьшится на , т.е. вектор , соответствующий точке пересечения вектора отрицательной вещественной полуоси, имеет такую же фазу, что и вектор . Искомым вектором  является вектор OE, равный по фазе OD. И так как OE > OD, увеличивающейся амплитуде соответствует неравенство:

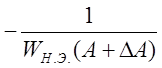 >      (7)

Это означает, что при ; , т.е. годограф  пересекает ось абсцисс слева от точки ( - 1; j0 ). Следовательно, цикл неустойчив и амплитуда продолжает увеличиваться.

При уменьшении амплитуды ON > OM, или 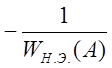 > , т.е. , НСАР устойчива и колебания продолжают затухать – система устойчива в малом. Итак, предельный цикл, соответствующий точке пересечения В, неустойчив.

В точке С, наоборот, увеличивающейся амплитуде соответствует неравенство OG > OF, т.е.  > , .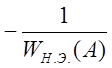

Следовательно, НСАР устойчива, колебания затухают. САР стремится возвратиться в точку С. Значит, точка С соответствует устойчивому предельному циклу.

Можно сформулировать следующее правило для определения устойчивости автоколебаний:

Если вблизи от точки пересечения векторов  и  при увеличении амплитуды колебаний АФЧХ линейной части охватывает обратную (инверсную) характеристику нелинейного элемента, то точке пересечения соответствует неустойчивый предельный цикл. Если же вблизи от точки пересечения  и  при увеличении амплитуды колебаний АФЧХ линейной части не охватывает обратную характеристику нелинейного элемента, то точке пересечения соответствует устойчивый предельный цикл.

Для определения устойчивости автоколебаний существует следующее правило:

Если вблизи от точки пересечения векторов  и  при увеличении амплитуды колебаний мы входим в контур АФЧХ линейной части, точка пересечения соответствует неустойчивым автоколебаниям. Если вблизи от точки пересечения векторов  и  при увеличении амплитуды колебаний мы выходим из контура АФЧХ линейной части, точка пересечения соответствует устойчивым автоколебаниям.