Оценка качества работы САР

Лекция 8    (6 часов)

ОЦЕНКА КАЧЕСТВА РАБОТЫ САР

Показатели качества работы САР

Устойчивость является необходимым, но недостаточным условием работоспособной системы, поскольку она (САР) должна отвечать дополнительным требованиям в статике и динамике для обеспечения хорошего функционирования, т.е. качественной работы. Под качеством САР понимают совокупность требований, прямо или косвенно характеризующих точность ее работы.

Требования в статике ориентированы на точность работы САР в установившихся режимах. При этом обычно необходимо, чтобы установившаяся ошибка САР e_уст не превышала заданных допустимых значений.

При анализе динамики САР предъявляются вполне определенные требования по отработке либо наиболее характерных управляющих воздействий, либо наиболее неблагоприятных. К числу неблагоприятных воздействий часто относят скачкообразное воздействие . Поскольку мы рассматриваем линейные системы, то изменение величины скачка K влияет только лишь на изменение масштаба по оси ординат, а перерегулирование s, время первого согласования t_c, время достижения переходным процессом максимального значения t_m, а также время регулирования t_p при этом остаются неизменными. Поэтому в качестве скачкообразного воздействия часто принимают единичную функцию Хевисайда .

Нам уже известно, что реакцию САР на единичное воздействие  называют переходной функцией . Следовательно, оценку качества работы САР можно осуществлять по переходной функции.

Разделим задачу оценки качества работы САР на две подзадачи:

1)  Оценка точности работы САР в установившихся режимах;

2)  Анализ качества переходных процессов в САР.

Оценка точности работы САР в установившихся режимах

Коэффициенты ошибок

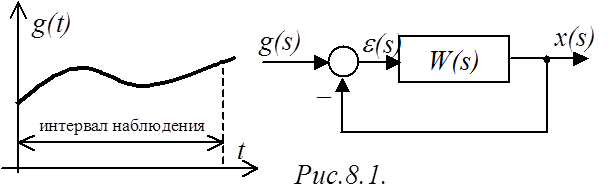При рассмотрении вопросов точности будем считать, что на систему с единичной отрицательной обратной связью действует управляющее воздействие, которое изменяется достаточно плавно при больших временах наблюдения (рис.8.1), т.е. так, что существенное значение имеют только первые l производных от  –

, , …, ,

а остальные, высшие производные  могут быть приняты равными нулю.

Наиболее полной характеристикой качества системы в установившемся режиме является установившаяся ошибка. Найдем ПФ САР по ошибке:

          .

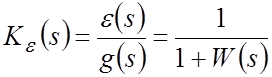Разложим  в ряд Маклорена, сходящийся при малых s (т.е. при больших временах t):

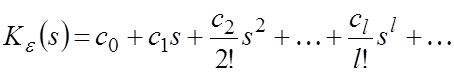              ,                        (1)

где коэффициенты ряда c₀, c₁, c₂, … определяются по уравнению [1]:

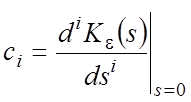              ,                        (2)

где значению i=0 соответствует отсутствие дифференцирования.

Действительно, из (1) с помощью (2) можно получить:

          ;

          ;

          …………………………………

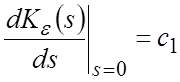Ограничиваясь в (1) первыми l+1 слагаемыми (т.е. пренебрегая производными порядка выше l-го), для изображения ошибки запишем выражение:

          ,

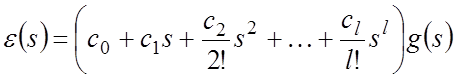или, переходя к оригиналам:

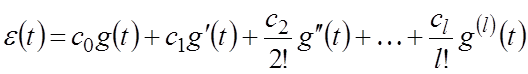                        .                        (3)

Коэффициенты c₀, c₁, …, c_l называются коэффициентами ошибок.

Коэффициенты ошибок определяют долевое участие в общей ошибке самого сигнала (c₀) и l его производных (c₁, c₂, …, c_l). Если входная  и выходная  величины одной размерности, то c₀ есть безразмерная величина, размерность c₁ – секунда (с), размерность c₂ – с² и т.д.

Первые три коэффициента ошибки, которыми часто и ограничиваются на практике, имеют специальные названия:  c₀ – коэффициент позиционной ошибки;  c₁ – коэффициент скоростной ошибки;  c₂ – коэффициент ошибки по ускорению.

Примечание. Только что рассмотрен случай, когда на САР действует только управляющее воздействие , поэтому, строго говоря, выше речь шла о коэффициентах ошибки по управляющему воздействию. В случае действия на САР дополнительного возмущающего воздействия  в силу линейности рассматриваемых САР

            .

При учете второго слагаемого аналогичным образом могут быть введены коэффициенты ошибки по возмущающему воздействию.

Коэффициенты ошибок в статических и астатических САР

Рассмотрим статическую систему (). Как известно, при отработке постоянного управляющего воздействия  (рис.8.2) в ней имеет место установившаяся ошибка

,

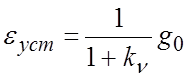где  – коэффициент усиления разомкнутой САР.

Производные первого и высших порядков сигнала  равны нулю:

          ,  ,  ,  …

При больших временах t (в т.ч. в установившемся режиме, т.е. при ) установившаяся ошибка, согласно (3), равна

          .

Сравнивая последние два выражения для установившейся ошибки, получаем, что коэффициент ошибки

          .

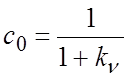Астатические системы (), как было показано раньше, постоянный управляющий сигнал  (рис.8.2) отрабатывают без ошибки в установившемся режиме:

          .

Следовательно, для любой астатической системы коэффициент ошибки c₀ равен нулю:

                        .                        (4)

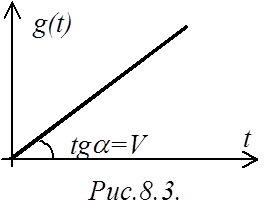Рассмотрим астатическую систему 1-го порядка (). Подадим на ее вход линейно изменяющийся сигнал  (рис.8.3). Производные: , .

Согласно (3) и с учетом свойства (4) астатических САР, установившаяся ошибка может быть записана в виде:

          .

Вспоминая понятие добротности по скорости , определяем, что коэффициент ошибки c₁ в астатической системе 1-го порядка равен

          ,

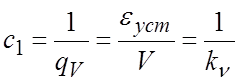где  – коэффициент передачи разомкнутой САР.

Таким образом, в астатической системе 1-го порядка коэффициент ошибки c₁ по скорости изменения задающего воздействия есть величина, обратная добротности САР по скорости.

Астатические системы 2-го порядка () линейно изменяющееся управляющее воздействие  (рис.8.3) отрабатывают без установившейся ошибки, поэтому для них, кроме условия (4),

              .                        (5)

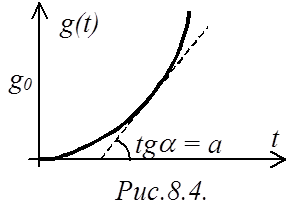
Подадим на вход астатической системы 2-го порядка воздействие, изменяющееся в квадратичной зависимости от времени (с постоянным ускорением),  (рис.8.4). Производные , , .

Поэтому установившаяся ошибка с учетом (3) – (5) равна

          .

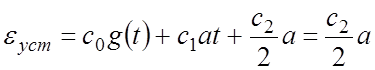С другой стороны, вспоминая понятие добротности по ускорению , определяем, что коэффициент ошибки c₂ в астатической системе 2-го порядка равен

          .

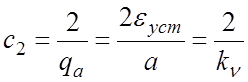Таким образом, в астатической системе 2-го порядка коэффициент ошибки c₂ по ускорению изменения задающего воздействия есть величина, обратная половине добротности САР по ускорению.

Для астатических систем более высокого порядка () рассуждения проводятся аналогично.

Определение некоторых коэффициентов ошибок

по ЛАЧХ разомкнутой САР

Точность работы САР в установившихся режимах связана с характером изменения ЛАЧХ разомкнутой системе в области низких частот (т.е. с ее наклоном в самой левой области частот). Суть определения коэффициентов ошибок по ЛАЧХ разомкнутой САР -го порядка состоит в определении частоты, при которой низкочастотный участок ЛАЧХ пересечет ось частот, равной

          ,

где  – коэффициент ошибки при отработке управляющего воздействия, представляющего собой кривую -го порядка вида . При этом коэффициенты ошибок c₀, c₁, …, c_n–1 будут равны нулю.