Зная время достижения переходной функцией максимального значения
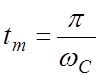 ,
,
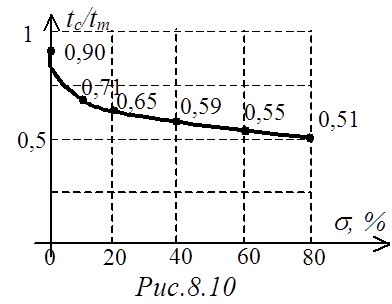 можно приближенно с помощью зависимости рис.8.10 [3] определить время
первого согласования tc.
можно приближенно с помощью зависимости рис.8.10 [3] определить время
первого согласования tc.
Если переходный процесс в САР завершается после 1 – 2 колебаний, то время переходного процесса может быть определено по приближенной зависимости:
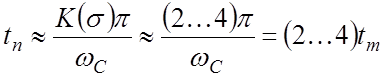 .
.
Оценка качества работы САР
по резонансному максимуму АЧХ замкнутой системы
Определение резонансного максимума по ЧХ разомкнутой САР
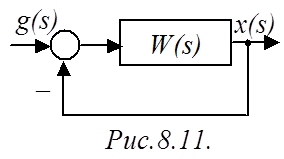 Пусть имеется САР, изображенная на рис.8.11.
Пусть имеется САР, изображенная на рис.8.11.
Частотная (или, как ее еще называют, амплитудно-фазовая) характеристика замкнутой системы:
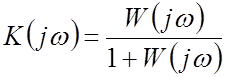
Амплитудно-частотная характеристика (АЧХ):
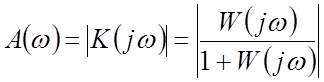 (1)
(1)
Примерный вид нормированной АЧХ представлен на рис.8.12.
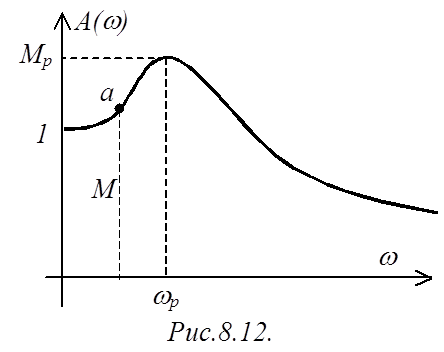 Чем выше резонансный максимум Mp, тем меньше запас устойчивости, и тем больше
склонность системы к колебаниям. В реальных САР величина Mp находится в пределах 1,0…1,8.
Чем выше резонансный максимум Mp, тем меньше запас устойчивости, и тем больше
склонность системы к колебаниям. В реальных САР величина Mp находится в пределах 1,0…1,8.
Возьмем на АЧХ некоторую точку а (рис.8.12), значение АЧХ в ней обозначим через М.
Отобразим точку а на комплексную плоскость
частотной характеристики разомкнутой САР. Для этого в формуле (1) подставим ![]() :
:
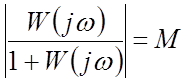 (2)
(2)
Частотная характеристика разомкнутой САР в точке а может быть определена в виде:
![]() ,
,
и тогда
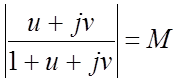 . (3)
. (3)
Решая уравнение (3) относительно u и v, можно прийти к выводу, что линия равных значений М отображается на плоскость ЧХ разомкнутой САР в окружность, уравнение которой:
![]() , (4)
, (4)
где
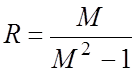 – радиус окружности;
– радиус окружности; 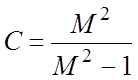 – смещение центра окружности по оси
абсцисс.
– смещение центра окружности по оси
абсцисс.
Построив семейство таких окружностей (рис.8.13) для разных значений 1<М<¥, замечаем, что при M®¥ радиус окружности R®0 и окружность вырождается в точку с координатами (–1; j0). С другой стороны, при М®1 радиус R®¥, и окружность вырождается в линию, параллельную оси ординат и отстоящую от нее на 0,5.
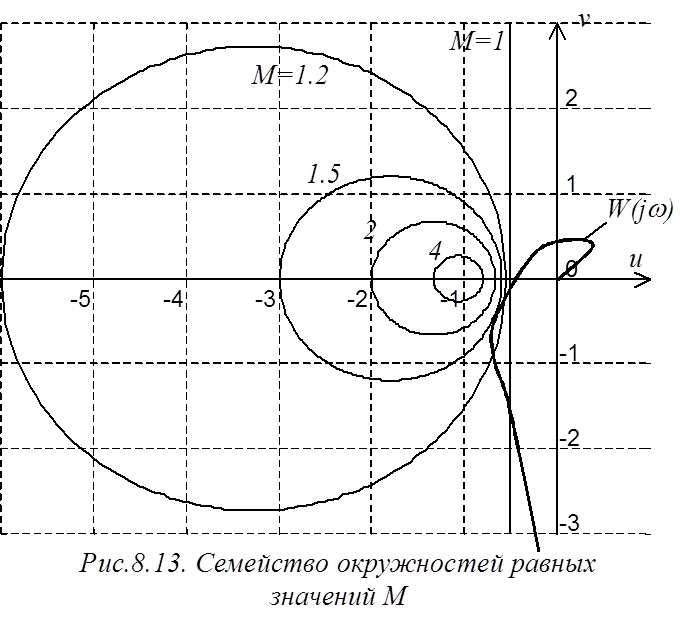
Можно отметить, что для значений 0<M<1 получится семейство окружностей, расположенный справа
от прямой М=1 ![]() симметрично с первым
семейством. При М=0 окружность вырождается в точку, совпадающую с
началом координат.
симметрично с первым
семейством. При М=0 окружность вырождается в точку, совпадающую с
началом координат.
Величина резонансного максимума может быть определена путем нахождения окружности, которой касается ЧХ разомкнутой САР (совпадает только в одной точке). Например, САР, ЧХ которой в разомкнутом состоянии имеет вид W(jw) (рис.8.13) будет иметь резонансный максимум Мр=1.5.
Проектирование САР с заданным уровнем Мр
 На практике очень часто ставят задачу: спроектировать
систему, для которой Мр будет не больше некоторого заданного
значения Mзад.
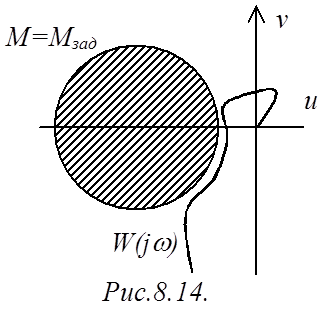
Очевидно, что в общем случае задача будет решена, если обеспечить такой вид ЧХ
разомкнутой системы, чтобы ее кривая не заходила внутрь окружности М=Мзад
(рис.8.14). Таким образом, окружность М=Мзад ограничивает запретную
зону для амплитудно-фазовой характеристики (заштрихована).
На практике очень часто ставят задачу: спроектировать
систему, для которой Мр будет не больше некоторого заданного
значения Mзад.
Очевидно, что в общем случае задача будет решена, если обеспечить такой вид ЧХ
разомкнутой системы, чтобы ее кривая не заходила внутрь окружности М=Мзад
(рис.8.14). Таким образом, окружность М=Мзад ограничивает запретную
зону для амплитудно-фазовой характеристики (заштрихована).
Рассмотрим частный случай. Пусть Мзад=2.
Решение.
По заданной величине Мзад определяем координаты радиуса и центра окружности:
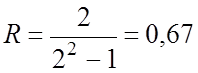 ;
; 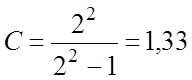 .
.
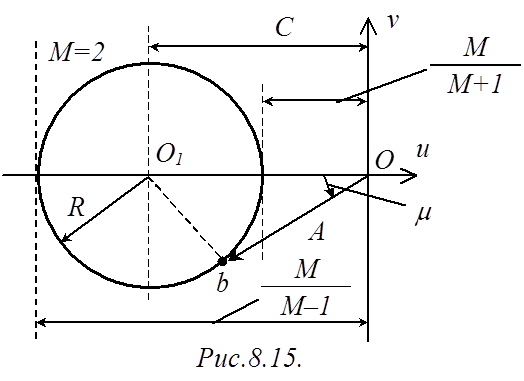 Строим окружность с центром в точке (–1,33; 0) радиуса
0,67 (рис.8.15).
Строим окружность с центром в точке (–1,33; 0) радиуса
0,67 (рис.8.15).
Чтобы реальное значение резонансного максимума было меньше заданного, необходимо, чтобы ЧХ разомкнутой САР не заходила в запретную зону, т.е. внутрь окружности.
Пусть точка b принадлежит ЧХ разомкнутой САР. Обозначим угол, который образует вектор А, проведенный из начала координат в точку b, с отрицательным направлением оси u, через m. Очевидно, что угол m равен запасу устойчивости САР по фазе.
Из рис.8.15 следует, что запретная зона может иметь место при значении модуля АЧХ А разомкнутой системы
![]()
или
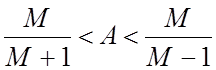 . (5)
. (5)
Очевидно также, что для любого модуля А существует такой угол m, при котором ЧХ разомкнутой системы не заходит в запретную зону.
Из треугольника ObO1 можно найти выражение для запаса по фазе, при котором ЧХ может попасть в запретную зону:
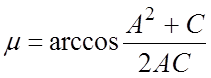 . (6)
. (6)
Используя (6), можно построить называемые m-кривые (рис.8.16) [1], пользуясь которыми, для любого значения модуля А можно найти то значение величины m, при котором обеспечивается требуемое значение резонансного максимума.
Для зависимости (6) можно определить, что максимум
будет иметь место при ![]() , а само значение
максимума:
, а само значение
максимума:
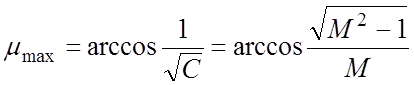 . (7)
. (7)
Если имеются логарифмические частотные характеристики разомкнутой системы, то по имеющимся m-кривым и при заданном значении М можно построить требуемое значение запаса по фазе для каждого значения модуля А, удовлетворяющего условию (5), которое для ЛАЧХ принимает вид:
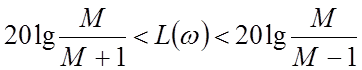 . (8)
. (8)
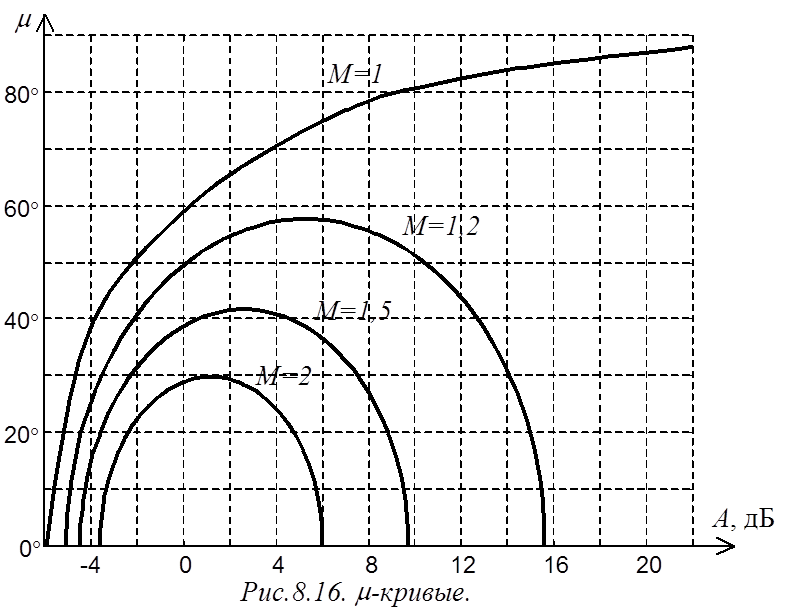
В результате можно получить запретную зону для ЛФЧХ. Чтобы показатель колебательности Мр не был больше заданного значения, ЛФЧХ не должна заходить в эту область.
Определим условия, при которых ЛФЧХ гарантированно не заходит в запретную область, на примере типовой ЛАЧХ типа "–2–1–2".
Пусть передаточная функция разомкнутой САР равна
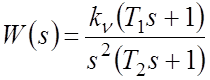 , (9)
, (9)
причем
![]() .
.
Логарифмические частотные характеристики такой разомкнутой САР представлены на рис.8.17.
Выражение для ЛФЧХ для (9) имеет вид:
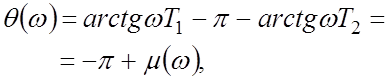
где
![]() – запас по фазе, который запишем
следующим образом:
– запас по фазе, который запишем
следующим образом:
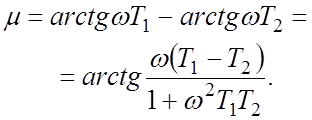 (10)
(10)
Для
зависимости (10) можно определить, что ее максимум будет иметь место при 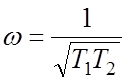 , а само значение максимума:
, а само значение максимума:
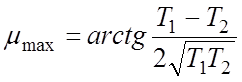 . (11)
. (11)
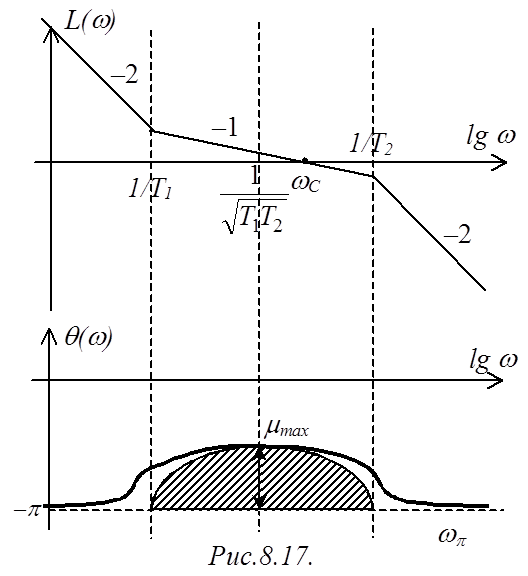
Таким образом, максимальный запас по фазе определяется только постоянными времени, определяющими участок с наклоном "–1".
 В [1]
доказано, что значение максимального запаса по фазе (11) будет не меньше
предельно допустимого запаса по фазе (7) при условии:
В [1]
доказано, что значение максимального запаса по фазе (11) будет не меньше
предельно допустимого запаса по фазе (7) при условии:

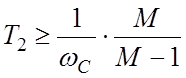
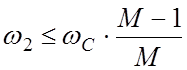
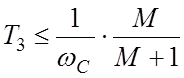
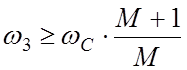 (12)
(12)
В граничном случае (равенство) ЛФЧХ будет касаться запретной зоны в точке m=mmax. В этом случае будет иметь место максимальное быстродействие системы при заданном уровне Мр.
Таким образом, при выполнении условий (12) для ЛАЧХ разомкнутой системы вида "–2–1–2" требования по величине Мр будут выполнены.
В случае, когда ЛАЧХ разомкнутой системы имеет вид "–2–1–2–3–4…", также можно пользоваться представленными зависимостями, предварительно заменив все апериодические звенья с частотами сопряжения правее частоты среза одним апериодическим звеном с постоянной времени TS, равной сумме постоянных времени этих звеньев.
В этом случае второе условие принимает вид:
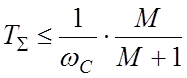 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.