На рис.8.5 изображены начальные (низкочастотные) участки ЛАЧХ статической и астатических (n=1, 2, 3) САР и указаны коэффициенты ошибок при отработке указанного воздействия.
При более сложных (полиномиальных) законах изменения управляющего воздействия следует пользоваться формулами (1) и (2) (что иногда очень затруднительно), либо воспользоваться следующим алгоритмом.
Определение коэффициентов ошибок
по передаточной функции САР по ошибке
Пусть имеется ПФ системы по ошибке:
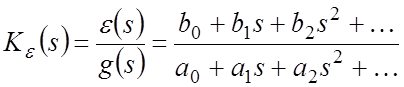
Коэффициенты ошибок в общем виде можно определить, если числитель этой ПФ разделить на знаменатель (по правилу деления полиномов), а затем сравнить полученный результат с равенством (1).
Для удобства выполнения операции деления полиномов рекомендуется члены делимого и делителя располагать в порядке увеличения степени s:
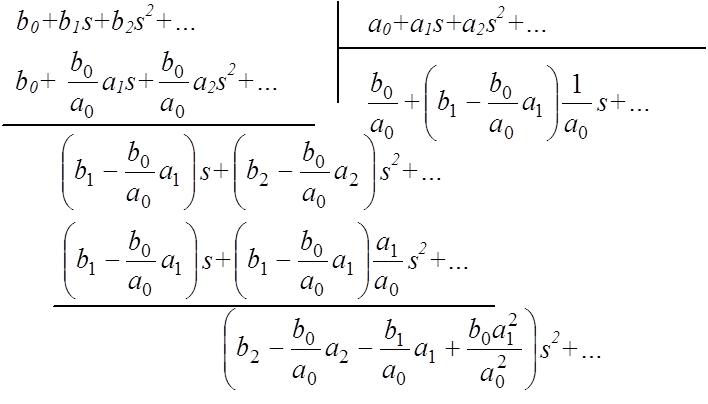
Деление выполняют до тех пор, пока либо остаток не становится равным нулю, либо при достижении нужного количества слагаемых в частном, позволяющих определить необходимые коэффициенты ошибок. Для определения же коэффициентов ошибок полученный результат сравнивается с выражением (1).
Пример. Передаточная функция разомкнутой системы имеет вид:
.
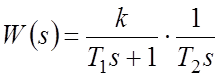Определить коэффициенты ошибок.
Решение. Определяем ПФ замкнутой системы по ошибке:
.
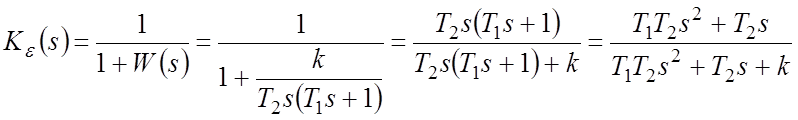Выполняем деление числителя на знаменатель:
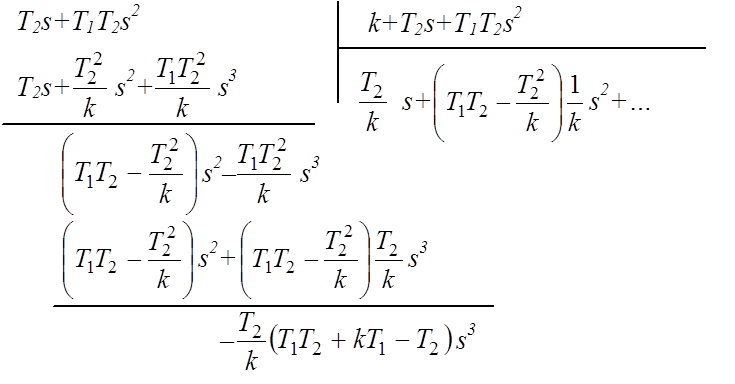
Сравнивая результат деления с (1), определяем:
; 
; 
.
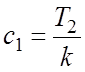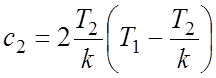Пусть задающее воздействие, действующее на систему, имеет вид:
.
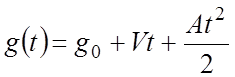Тогда установившаяся ошибка по (3) равна
.
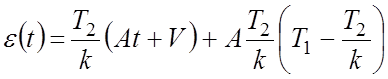Оценка качества переходных процессов
Существуют прямые и косвенные показатели качества в переходном режиме.
К прямым методам относят такие, в которых оценка качества дается по предварительно определенной (аналитически или с помощью математического моделирования) или снятой экспериментально переходной характеристике h(t).
В косвенных методах оценка дается на основе анализа частотных и некоторых др. характеристик системы. Они требуют менее громоздких вычислений, и поэтому более удобны. Косвенные методы подразделяют на корневые, частотные и интегральные.
Все методы оценки качества переходных процессов предполагают априори, что система является устойчивой.
Прямые методы оценки качества переходных процессов
К прямым показателям качества относят время регулирования и перерегулирование, определяемые по переходной характеристике.
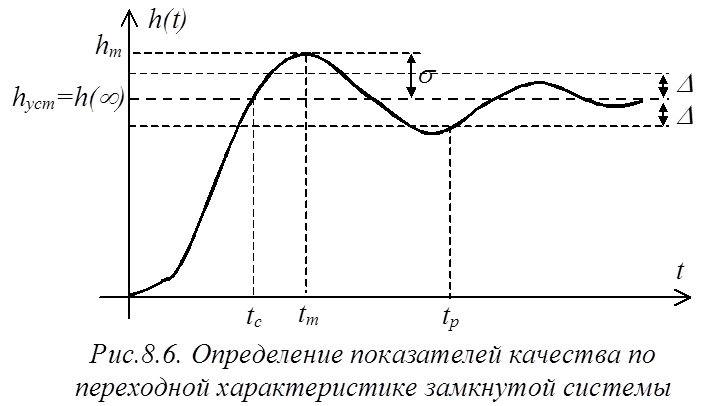
Временем регулирования tp называют время, по истечении которого отклонение выходной величины от установившегося значения не превышает некоторой заданной величины D. Обычно принимают D= (0,01…0,05)hуст.
Перерегулированием s называют максимальное отклонение переходной функции от установившегося значения, выраженное в процентах:
.
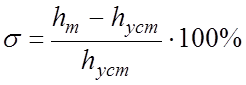В большинстве случаев процесс считается устойчивым, если величина перерегулирования не превышает 10…30%.
Кроме tp и s, иногда в качестве показателей качества рассматривают время первого согласования tс (которое определяет быстродействие системы) и число колебаний Nк выходной величины относительно установившегося значения за время tp (обычно не должно превышать 1…2).
О взаимосвязи ЛАЧХ разомкнутой системы
с качеством переходного процесса
Для оценки качества переходного процесса может быть использована связь между характером переходного процесса и формой ЛАЧХ.
Низкочастотная часть ЛАЧХ связана с работой САР в установившихся режимах (при больших временах наблюдения) и характеризует точность работы системы.
Высокочастотный участок ЛАЧХ определяет начальный участок переходного процесса.
Среднечастотная часть ЛАЧХ определяет качество работы системы в переходных режимах. В этой области находится частота среза wС, определяющая быстродействие системы; по значению ЛФЧХ при частоте среза можно определить запас устойчивости по фазе. По значению частоты среза с помощью эмпирических зависимостей можно определить время первого согласования tc, время достижения максимального значения tm и время регулирования tp, т.е. основные параметры переходного процесса. Эти эмпирические зависимости носят название номограмм Честната и Майера [4], и будут использоваться нами в дальнейшем.
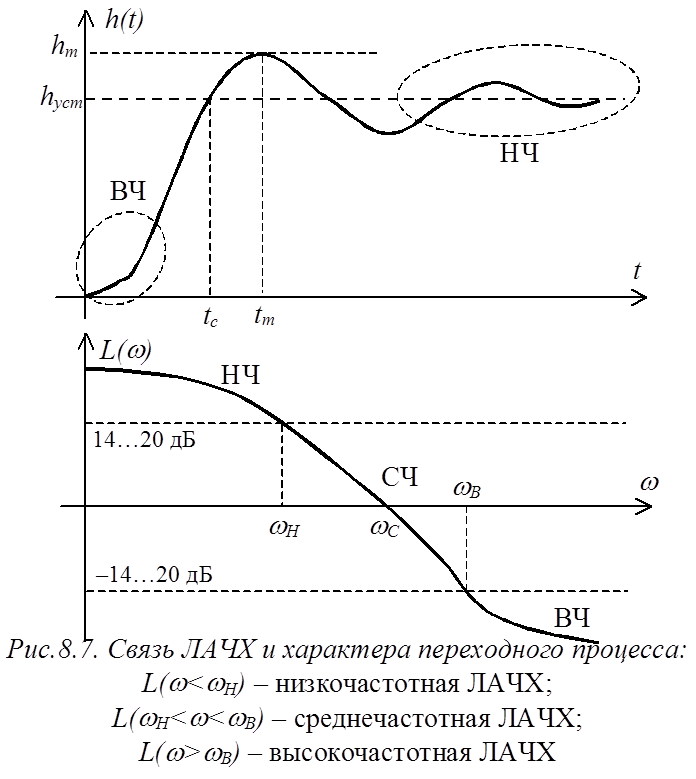
Любая работоспособная система имеет среднечастотный участок ЛАЧХ в области частоты среза wС с наклоном –1. Только при этом условии можно получить качественную САР, причем чем больше длина среднечастотного участка с наклоном –1, тем больше вероятность получения качественной системы, с приемлемыми колебательностью и перерегулированием.
Некоторые следствия из анализа номограмм Честната и Майера:
1. Смещение ЛАЧХ вдоль оси частот влево или вправо влияет только на быстродействие САР. Чем больше частота среза wС, тем система более быстродействующая:
.
2. Если в области высоких частот имеется наклон ЛАЧХ –2, –3, –4 и т.д., то высокочастотный хвост этой ЛАЧХ можно заменить добавлением ЛАЧХ апериодического звена с постоянной времени TS, равной сумме постоянных времени всех апериодических звеньев, частоты сопряжения которых находятся правее частоты среза (рис.8.8).
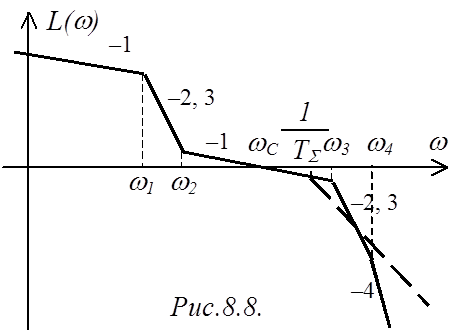Другими словами, все непрерывные звенья, постоянные времени которых
малы (частоты сопряжения выше частоты среза), могут быть заменены апериодическим
звеном с передаточной функцией
,
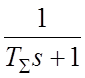где
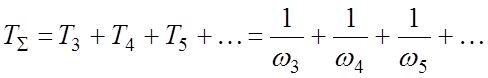
Частотные показатели качества переходных процессов
Исходя из того, что качественная САР должна быть прежде всего устойчивой, в качестве частотных показателей качества рассматриваются уже известные нам запас устойчивости по амплитуде А и запас устойчивости по фазе y, а также резонансный максимум АЧХ замкнутой системы Мр и полоса пропускания (рис.8.9).
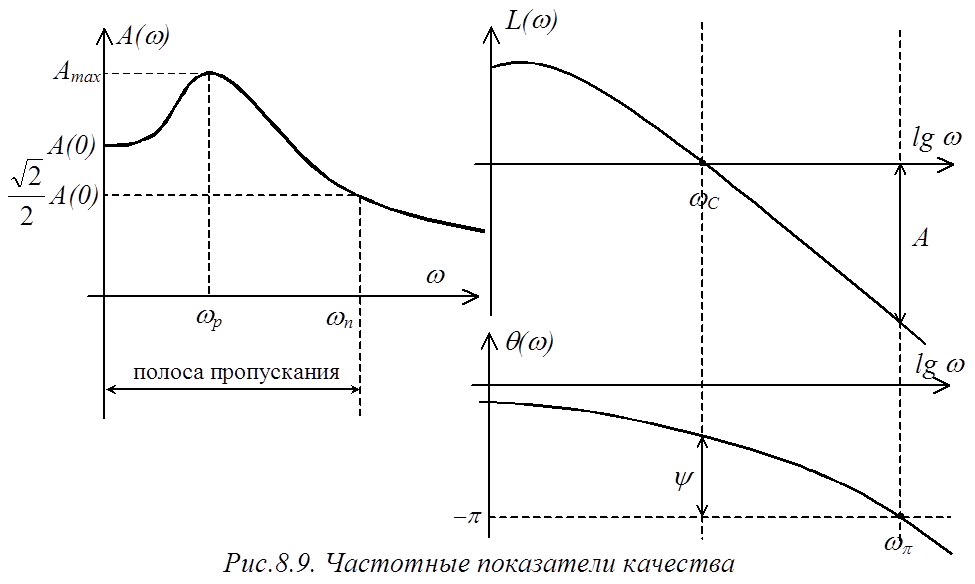
Запасы устойчивости по амплитуде и по фазе характеризуют близость системы к границе устойчивости и определяются по логарифмическим частотным характеристикам разомкнутой САР. Чем дальше система от границы устойчивости, тем она лучше. В качественных системах запасы устойчивости должны составлять:
А=6…20 дБ y=30…60°.
Резонансный максимум является показателем колебательности САР, и, как будет показано ниже, позволяет более удобно оценивать запас устойчивости САР. Резонансный максимум равен отношению максимального значения Amax АЧХ замкнутой системы, которое имеет место при резонансной частоте wр, к ее начальному значению A(0). Другими словами, показатель колебательности есть максимальное отношение амплитуд выходного xmax и входного gmax воздействий, имеющее место при частоте задающего воздействия w=wр, определяемой экспериментальным или расчетным путем:
.
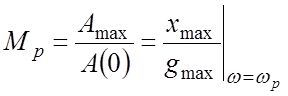Обычно в качественных системах показатель колебательности не должен превосходить значений 1,1…1,5.
Для оценки величины резонансного максимума можно пользоваться эмпирическими формулами связи между запасом устойчивости по фазе и резонансным максимумом:
,
а также связи между резонансным максимумом и перерегулированием (s в долях):
.
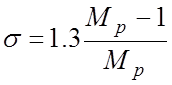
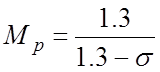Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.