Основные понятия метрологии. Классификация измерений. Абсолютная и относительная погрешность измерений. Виды (природа) погрешности измерений физических величин. Прямое равноточное измерение и его нормирование метрологические характеристики.

1. Основные понятия метрологии.

Метрология — это наука об измерениях, их видах, методах и средствах, обеспечении единства измерений (ОЕИ), способах достижения требуемой точности. В метрологии различают три направления: теоретическое (фундаментальное), законодательное (правовое) и практическое (прикладное).

Базовыми понятиями метрологии и измерительной техники являются измерение, единство измерений, точность измерений .

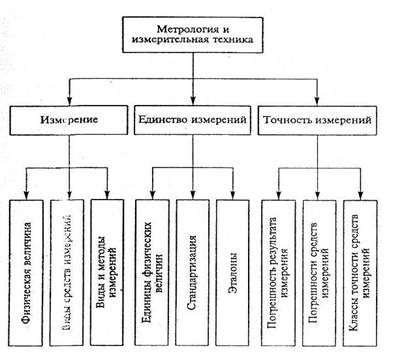
2. Классификация измерений.

Физическую величину можно классифицировать по множеству признаков.

По точности проведения измерений

По виду измеряемой величины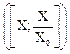

По природе измеряемых физических величин (Механические, электрические, магнитные)

По уравнению измерений

- Y искомая величина; X – искомая Такое измерение называется прямым.

 причем  известно. Такое измерение называется косвенным.

 когда неизвестен, тогда  - совместное измерение.

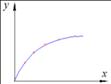
Результатом совместного измерения является построение таблиц, а также графика или экспериментального поля точек.

3. Абсолютная и относительная погрешность измерений.

Абсолютная погрешность может быть и “+” и “-”. Поскольку,  как правило, не известно, вводится оценка истинного значения, которая называется действительной величиной . Существуют различные приемы введения , чаще всего в качестве действительной величины при измерении Х берется среднее арифметическое по серии измерений

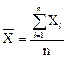 (6)

Тогда ∆ прямых измерений Х будет:  (7)

Электроизмерительные приборы при их использовании (Амперметр включается последовательно, а вольтметр параллельно) вносят погрешность в измерения. Погрешность, вносимая ЭИП называется его приведенной погрешность, которая измеряется в %.

 Относительной погрешностью i измерения  является величина, определяемая формулой: 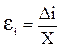 (8). Приведенная погрешность ЭИП определяется выражением: 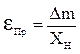 , где

 - номинальное значение измеренного значения - максимальная абсолютная погрешность. Максимальная погрешность возникает при использовании шкального участка шкалы.

Опр. Классом точности ЭИП называется верхняя граница его приведенной погрешности в соответствии с установленной классификацией.

Классы точности ЭИП: 0,05; 0,1; 0,5; 1; 1,5; 2; 2,5; 4.

Условно эти классы разбиваются на 3 группы.

0,05; 0,1; 0,5; – группа высококлассных (Прецизионные)

1; 1,5; 2; –  Контрольно-поверочные ЭИП

2,5; 4; – технические ЭИП

Приборы, имеющие приведенную погрешность более 4%, не допускаются к эксплуатации.

4. Виды (природа) погрешности при измерений физических величин.

По своей природе погрешности измерений можно разделить на 3 группы.

Систематические погрешности, которые определяются методикой и методологией. Систематические погрешности определяются так же суммарной приборной погрешностью измеряемых величин.

Личностная природа погрешности (человеческий фактор)

Случайная погрешность, зависящая от многих факторов, меняющаяся со временем. Для учета случайной погрешности разработана математическая теория ошибок (погрешность), использующая методы теории вероятности и математической статистики. В этой теории употребляются нормированные характеристики погрешности случайного характера.

Погрешности личного характера выявляются и устраняются административными мерами. Сложнее всего выявить и учесть погрешности систематического характера, поскольку для каждого случая она проявляется особым образом. За исключением прямого равноточного измерения Y=X. В этом случае систематическая погрешность легко устанавливается по классу точности использованного прибора 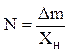; (1)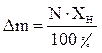

Случайная погрешность определяется методами теории ошибок .

Суммарная погрешность определяется по формуле:  (2)

Погрешность измеряется не алгебраически, а геометрически.

В случае, если одна из составляющих погрешности значительно больше другой, то одной из них можно пренебречь.

5. Прямое равноточное измерение и его нормирование метрологические характеристики.

При этом считаем, что значение Х неизвестно.

Для определения действительного значения измеряемой величины , которое является оценкой истинного её значения проводится серия измерений одним и тем же измерительным прибором и строится таблица измеренных значений.

Для оценки  вводится первая метрологическая нормированная характеристика – среднее арифметическое значение 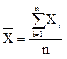. Для данной серии измерений найденное  и будет действующим значением . При этом выполняется следующее правило, установленное опытным путём: чем больше проведено измерений, тем ближе действительное значение приближается к истинному.

Второй метрологической характеристикой является

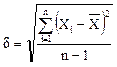Третьей метрологической нормированной характеристикой является  - средняя лв. погрешность по серии измерений . Для данной серии измерений  является некоторой постоянной величиной. Иногда кроме  учитывается дисперсия . Дисперсия определяет степень разброса измерений (измеряемых величин) относительно среднего арифметического. Величина  дает оценку погрешности случайного характера, измеряемой величины Х по всей серии измерений. Сами однократно измеренные значения  в силу разнообразных случайных причин не намного отличаются друг от друга, поэтому сама измеряемая величина ведёт себя случайным образом и называется случайной величиной.

При проведении другой серии измерений с большей или меньшей n будет меняться действующее значение искомой величины, т.е. её среднее арифметическое , поэтому  так же является величиной случайной и для оценки её погрешности вводится  - среднее арифметическое от средней квадратической погрешности и определяется по формуле: .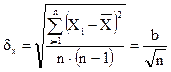

Математическое ожидание измеряет величина M, которая представляет собой некоторый заранее оговорённый интервал, в который входят измеряемые величины с тем или иным значением вероятности, которая называется доверительной вероятностью P. , где  - максимально допустимая абсолютная погрешность измерения, которая называется границей доверительного интервала или просто доверительным интервалом, при этом доверительный интервал однозначно связан с доверительной вероятностью P определенной интегральным соотношением.

Вывод: таким образом математическое ожидание измеренной величины Х по данной проведённой серии измерений даёт оценку истинного значения измеряемой величины, а так же максимальную допущенную погрешность измерений, т.е. ;

Нахождение H является целью прямого равноточного измерения.

6. Плотность распределения вер-тк случайной величины или закон её распределения f(x)

- закон распределения случайной величины, этот закон получается экспериментально в процессе прямых измерений и сводится к построению графика, называемого гистограммой прямого измерения. График строится в прямоугольной системе координат, вдоль оси абсцисс измеренного значения х, а по оси ординат частота появления -того или измеренного значения X.

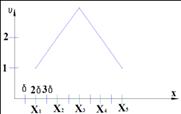
При этом ось x разбивается на ряд малых одинаковых участков  называемых шагом измерительной величины х. Частота появления очень малых измеренных значений, а также появление больших измеренных значений близких к 0.

Функцией распределения величины x будет называться непрерывная кривая, оптимальным образом проходящая вблизи всех точек гистограммы. Кривая должна иметь уравнение, т.е. определяется аналогичным образом. Функция распределения результата прямого равномерного измерения имеет колоколообразный вид, т.е.