Основные понятия метрологии. Классификация измерений. Абсолютная и относительная погрешность измерений. Виды (природа) погрешности измерений физических величин. Прямое равноточное измерение и его нормирование метрологические характеристики., страница 2

Экстремум в виде максимального, определяющего центр распределения, по смыслу центр распределения определяет случайную величину х наиболее часто появляющегося при измерениях, которое представляет собой  по данной серии измерений. Сама функция  имеет вероятностный характер и определяет вероятность появления измеряемой величины в отдельной точке, поэтому иногда её называют плоскостью распределения случайной величины х. Функция распределения является 5-ой метрологической характеристикой прямого равноточного распределения.

7. Виды распределений. Нормальный закон распределения случайной величины (закон Гаусса).

В зависимости от вида гистограммы можно ввести следующие законы распределения случайной величины.

Равномерный закон распределения случайной величины.

Треугольный закон распределения случайной величины.

Трапецеидальный закон распределения случайной величины.

Нормальный закон распределения случайной величины, график имеет следующий вид.

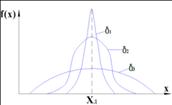
Каждая из кривых симметрична и отличается своей остротой >>

Немецкий математик Гаус нашёл аналитический вид нормального закона распределения случайной величины, проявляющегося при большом числе измерений или в серии большой выборки. Вид нормального закона распределения: .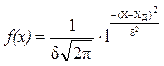

Свойства нормального закона распределения случайной величины:

Параметром функции распределения является , т.е. среднее квадратичное значение.

 в центре распределения, при всех других х правее или левее центра распределения вероятность такого значения х убывает.

Функция Гаусса симметрична относительно центра распределения, т.е. при измерениях появления как меньших так и больших значениях х относительно  равномерно.

Они показывают, что при серии измерений малой выборки закон распределения измеренной величины все более отклоняется т.е. видоизменяется относительно нормального закона.

8. Критерий нормальности распределения абсолютной погрешности при прямой измерений  физической величины Х.

Измеряется прямым равноточным методом (одним прибором) некоторая физическая величина Х, истинное значение которой нам неизвестно. В процессе эксперимента находится действительное значение , которое является оценкой её истинного значения. В качестве такой оценки при прямых значениях берётся , которое называется арифметическим средним 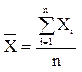. В процессе измерений находится абсолютная погрешность . При прямом равноточном измерении сами погрешности ведут себя как случайные величины, т.е. сами  должны мало отличаться друг от друга и тогда такие погрешности случайного характера подчиняются теории ошибок, и имеют различные виды распределения . В частности при проведении выборки оказалось что   подчиняется  нормальному закону распределения погрешности или закону Гаусса: 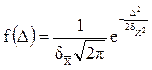 (1)

- абсолютная погрешность

- среднеарифметический от среднеквадратического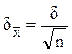

 - является общей оценкой среднего арифметического, которую можно рассматривать как случайную величину. Из формулы (1) видно, что центром распределения , который определяется наибольшим значением функции распределения, является значение .

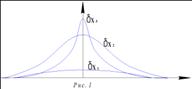
Из рис 1. можно сформулировать критерий “Нормальности” функции распределения .

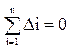 - нормальный закон.

9. Доверительная вероятность и доверительный интервал. Интервал вер-ти

Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной дове рителъной вероятностью

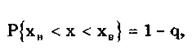
где q — уровень значимости; х_н, х_в— нижняя и верхняя границы интервала, находится истинное значение оцениваемого параметра

Для получения интервальной оценки нормально распределенной случайной величины необходимо:

• определить точечную оценку МО х̅ и СКО S_x случайной величины по формулам (6.8) и (6.11) соответственно;

• выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;

• найти верхнюю х_в и нижнюю х_н границы в соответствии с уравнениями

полученными с учетом (6.1). Значения х_н и х_в определяются из таблиц значений интегральной функции распределения F(t) или функции Лапласа Ф(1).

Полученный доверительный интервал удовлетворяет условию

           (6.13)

где n — число измеренных значений; z_p — аргумент функции Лапласа Ф(1), отвечающей вероятности Р/2. В данном случае z_p называется квантильным множителем. Половина длины доверительного интервала  называется доверительной границей погрешности результата измерений. В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Х_ц в интервал tS_x описывается неравенством Чебышева

где S_x — оценка СКО распределения; t — положительное число.

Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО. Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6S_X. Неравенство Чебышева дает в данном случае 3,16S_X. В связи с этим оно не получило широкого распространения. Смысл понятий "доверительный интервал" и "доверительная вероятность" состоит в следующем: пусть a =0.95, тогда можно утверждать с надежностью 95%, что истинное значение величины xист не отличается от оценки (3) больше, чем на ± D xсл.

10. Нормировка интеграла вероятности. 

Теоретически можно предположить существование погрешности в любом интервале её значений от <<, тогда вероятность появления при появлении любого конечного значения  обязательно попадает в этот интервал, т.е. это можно рассматривать достоверным событием. Тогда 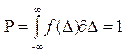(5) – условие нормировки интеграла вероятности по 1. Несобственный интеграл (5) численно равен площади криволинейной трапеции, ограниченной осью абсцисс и графиком подынтегральной функции.