31. Расчет добавочного сопротивления к вольтметру.
![]() - большое активное сопротивление,
включаемое последовательно с вольтметром для увеличения пределов его измерений.
По существу включение
- большое активное сопротивление,
включаемое последовательно с вольтметром для увеличения пределов его измерений.
По существу включение ![]() изменяет номинальное
значение вольтметра
изменяет номинальное
значение вольтметра ![]() .
.
Рассмотрим схему:
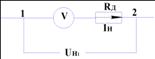
Между
токами 1 и 2 будет значение нового напряжения полепольного вольтметра, при этом
схема должна отклониться на всю шкалу, т.е. через вольтметр будет протекать ток
номинального отклонения, связанный с номинальным напряжением по формуле: ![]() .
.
Зададимся
коэффициентами преобразования номинального напряжения: ![]()
Для
последовательно соединённых элементов вольтметра и ![]() имеем
разность новые значения номинального напряжения:
имеем
разность новые значения номинального напряжения: ![]() ;
;
![]() ;
; ![]() ;
;
![]()
32. Измерение активного сопротивления метода амперметра и вольтметра.
Рассмотрим электрическую схему:
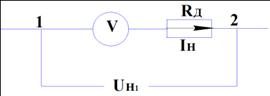
Возьмём
для измерения амперметр с достаточно малым внутреннем сопротивлением,
удовлетворяющим условию ![]() , тогда вольтметр
будет показывать входное напряжение :
, тогда вольтметр
будет показывать входное напряжение : ![]()
В
узле 1 происходит разделение неразветвлённого тока I, показываемого
амперметром, на ток ![]() и ток
и ток ![]() . Вольтметр и неизвестное
сопротивление Rх включены
параллельно, поэтому их общее сопротивление будет равно:
. Вольтметр и неизвестное
сопротивление Rх включены
параллельно, поэтому их общее сопротивление будет равно: 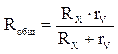 , тогда по закону Ома для участия 1 и
2 нужно записать:
, тогда по закону Ома для участия 1 и
2 нужно записать: ![]()
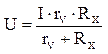 ;
; ![]() ;
;
![]() ;
; 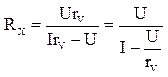 (4)-расчётная
формула истинного
(4)-расчётная
формула истинного ![]() . RX получится при
условии, что
. RX получится при
условии, что 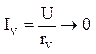 , а rv бесконечно
большой.
, а rv бесконечно
большой. 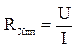 (5)
(5)
Поскольку
сопротивлением амперметра пренебрегаем всё напряжение падает на Rобщ., которое
связано следующим образом : 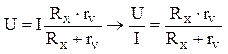 , тогда
относительная погрешность
, тогда
относительная погрешность 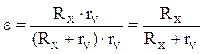 (6)
(6)
Из (6) следует, что погрешность что погрешность измерения Rx будет тем меньше, чем больше будет сопротивление вольтметра измеряемого сопротивления Rx, отсюда следует, что схема рис. 1 целесообразна для заведомо малых сопротивлений когда Rx << Rv
![]() . Тогда для измерения заведомо
больших сопротивлений целесообразна следующая электрическая схема:
. Тогда для измерения заведомо
больших сопротивлений целесообразна следующая электрическая схема:
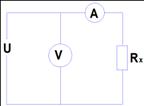
Независимо
от внутреннего сопротивления вольтметра он будет показывать приложенное
напряжение ![]() . Для простоты считаем, что
внутреннее сопротивление вольтметра бесконечно велико
. Для простоты считаем, что
внутреннее сопротивление вольтметра бесконечно велико ![]() ,
тогда в узле 1 ответвление тока в цепь вольтметра не будет и весь ток,
показываемый амперметром проходит через сопротивление RX. Тогда
,
тогда в узле 1 ответвление тока в цепь вольтметра не будет и весь ток,
показываемый амперметром проходит через сопротивление RX. Тогда 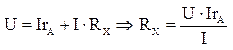 (7). Обычно предполагается, что
сопротивление амперметра мало, тогда
(7). Обычно предполагается, что
сопротивление амперметра мало, тогда 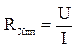 . Найдём
абсолютную погрешность определения RX при условии
пренебрежения сопротивлением амперметра.
. Найдём
абсолютную погрешность определения RX при условии
пренебрежения сопротивлением амперметра.  (8).
Из (8) видно, что погрешность при определении заведомо больших сопротивлений
будет тем меньше, чем меньше сопротивление амперметра.
(8).
Из (8) видно, что погрешность при определении заведомо больших сопротивлений
будет тем меньше, чем меньше сопротивление амперметра.
33. Измерение активного сопротивления с помощью вольтметра с известным внутренним сопротивлением.
Рассмотрим электрическую схему
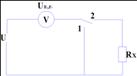
При
замыкании тока в катушке 1 вольтметр измерит входное напряжение ![]() .
.
При
замыкании тока в положении 2 показания вольтметра изменятся![]() ,
,
При
этом через вольтметр и неизвестное сопротивление ![]() ,
будет протекать одинаковый ток I. По закону Ома можно записать, что
входное напряжение:
,
будет протекать одинаковый ток I. По закону Ома можно записать, что
входное напряжение: ![]() ;
; 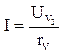 ,
тогда
,
тогда 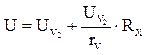 ;
; ![]()
![]() (9).
(9).
34. Измерение активного сопротивления амперметром в известным внутренним сопротивлением.
Рассмотрим электрическую схему.
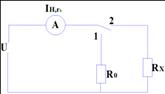
При
включении К в положение 1 амперметр будет показывать ток ![]() , который по закону Ома будет связан
с входным напряжением U по формуле:
, который по закону Ома будет связан
с входным напряжением U по формуле: ![]() (10).
При включении ключа в положении 2 амперметр покажет значение тока
(10).
При включении ключа в положении 2 амперметр покажет значение тока ![]() , которое будет связано с входным
напряжением по формуле:
, которое будет связано с входным
напряжением по формуле:
![]() (11). Приравнивая правые части (10)
и (11) получим:
(11). Приравнивая правые части (10)
и (11) получим: ![]() ;
; ![]() (12).
(12).
Формула
(12) даёт возможность косвенного определения значения ![]() по
двум измеренным значениям тока, известных значений
по
двум измеренным значениям тока, известных значений ![]() и
и
![]() .
.
35. Мостовой метод измерения активного сопротивления. Мостик Уитстона.
Рассмотрим схему постоянного тока (моста Уитстона).
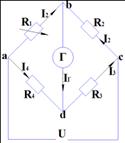
В
одну диагональ включён источник постоянного тока, а во вторую гальванометр
(прибор для измерения малых токов). Одно из сопротивлений ![]() берётся переменным. Зададимся
произвольным направлением токов в ветвях схемы. Схема позволяет определить
неизвестное сопротивление
берётся переменным. Зададимся
произвольным направлением токов в ветвях схемы. Схема позволяет определить
неизвестное сопротивление ![]() , включаемое в одно из плеч моста (например
, включаемое в одно из плеч моста (например ![]() ), остальные
сопротивления считаются известными. С помощью переменного резистора
), остальные
сопротивления считаются известными. С помощью переменного резистора ![]() добиваемся, условия
равновесия моста, при котором ток в цепи гальванометра становится равным 0.
добиваемся, условия
равновесия моста, при котором ток в цепи гальванометра становится равным 0. ![]() (13). Условие (13) будет
выполнено, когда станут равными потенциалы b и d:
(13). Условие (13) будет
выполнено, когда станут равными потенциалы b и d: ![]() (14). При выполнении условия (14)
ответвления токов в цепь гальванометра не происходит, откуда можно записать
(14). При выполнении условия (14)
ответвления токов в цепь гальванометра не происходит, откуда можно записать ![]() ,
, ![]() .
.
36. Мост переменного тока. Амплитудное и фазовое условие равновесия.
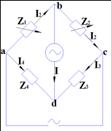
Для привидения моста переменного тока в положение равновесия нужны 2 регулировки.
В
частности эти сопротивления могут быть чисто реактивными в виде магазинов,
индуктивностей и емкостей. ![]() ;
; ![]() . Условие равновесия моста в общем виде
запишется следующим образом:
. Условие равновесия моста в общем виде
запишется следующим образом: ![]() (5);
(5); ![]() . Можно представить в показательной форме
. Можно представить в показательной форме ![]() (6), где Z – полное
сопротивление φ – фазовый множитель.
(6), где Z – полное
сопротивление φ – фазовый множитель.
Подставим
6 в 5: ![]() ;
; ![]() (7). Равенство 7
разделяется на два уравнения.
(7). Равенство 7
разделяется на два уравнения. ![]() (8);
(8); ![]() (9) – фазовое условие равновесия моста.
Показывает равновесие в каждом плече моста (фазовый сдвиг между токами и напряжением).
В частности если сопротивление всех плеч чисто активное, то все фазовые сдвиги
будут равны 0. Из условия (9) следует, что не любой мост переменного тока
может быть приведен к равновесию:
(9) – фазовое условие равновесия моста.
Показывает равновесие в каждом плече моста (фазовый сдвиг между токами и напряжением).
В частности если сопротивление всех плеч чисто активное, то все фазовые сдвиги
будут равны 0. Из условия (9) следует, что не любой мост переменного тока
может быть приведен к равновесию: ![]() ; Плечо 2 и 4 – чисто активные –
; Плечо 2 и 4 – чисто активные – 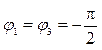 емкостная реактивность.
;
емкостная реактивность.
; 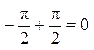 – «-» равенство
не получ., «+»- равенство получается. Нужно поменять емкость сопротивление на
индуктивное.
– «-» равенство
не получ., «+»- равенство получается. Нужно поменять емкость сопротивление на
индуктивное.
37. Разновидности мостов переменного тока.
38. Мост Сотти.
Мост Сотти для определения параметров конденсатора.
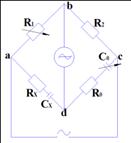
![]() - известное активное сопротивление
- известное активное сопротивление
![]() - известный магазин ёмкостей
- известный магазин ёмкостей
![]() ;
;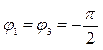 ;
;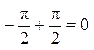 .
.
В
цепи переменного тока внутри конденсатора возникает меняющееся во времени
электрическое поле, это поле эквивалентно току проводимости в том смысле, что
оно является источником магнитного поля силовые линии которого охватывают
силовые линии переменного электрического поля. Существование электрического
переменного поля эквивалентно протеканию тока силу которого регистрирует А.
Этот ток в отличие от токопровод. называется током смещения. Используем условие
равновесия моста в общем виде для определения ![]() .
.
![]() ;
; 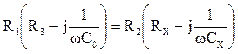 ;
;
![]() ;
; ![]()
Приравниваем
мнимые части ![]() ;
; ![]() -
значение магазина ёмкостей после привидения моста в состояние равновесия.
-
значение магазина ёмкостей после привидения моста в состояние равновесия.
39. Мост Вина.
Rx – активное
сопротивление провода катушки, Lx – неизвестная индуктивность катушки. Условие
равновесия в общем виде:![]() Найдем Lх и Rx.
Найдем Lх и Rx. ![]()
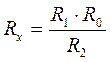
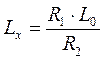
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.