Определение передаточной функции системы управления, представленной структурной схемы. Определение передаточной функции для заданной системы и отображение полюсов системы на комплексной плоскости

СОДЕРЖАНИЕ

	Задание 1	4
	Задание 2	7
	Заключение	26
	Литература	27
	Приложение А	28

Задание 1

Определение передаточной функции системы управления, структурная схема которой представлена на рисунке 1

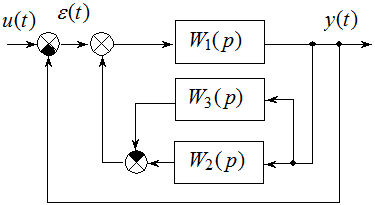
Рисунок 1 – Структурная схема СУ

Соединение блоков с передаточными функциями и  представляет собой соединение с отрицательной обратной связью.

Передаточная функция этих блоков  будет определяться по формуле

.

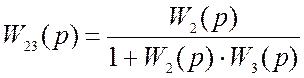Блоки с передаточными функциями и представляет собой соединение с положительной обратной связью.

Передаточная функция этих блоков  будет определяться по формуле

.

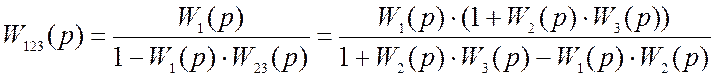Передаточная функция всей системы будет определяться по формуле

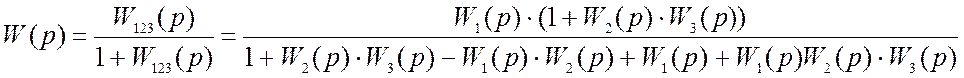
При подстановке числовых значений передаточная функция системы примет вид

.

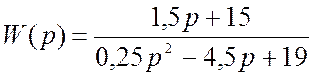Определение типов звеньев

1)Звено с передаточной функцией 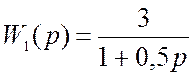 – апериодическое звено.

Общий вид передаточной функции

,

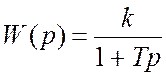где  – коэффициент усиления данного звена;

 – постоянная времени.

Для данного звена коэффициенты 

, .

2) Звено с передаточной функцией 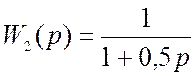 – апериодическое звено.

Общий вид передаточной функции

,

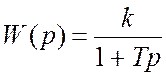где  – коэффициент усиления данного звена;

 – постоянная времени.

Для данного звена коэффициенты 

, .

3) Звено с передаточной функцией  – безынерционный усилитель.

Общий вид передаточной функции

,

где  – коэффициент усиления данного звена;

Для данного звена коэффициент 

.

Определение дифференциального уравнения, которым описывается система

,

,

.

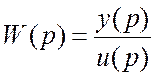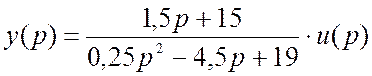Окончально дифференциальное уравнение примет вид

.

Задание 2

Определение передаточной функции системы управления, структурная схема которой представлена на рисунке 2

Передаточная функция блока .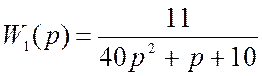

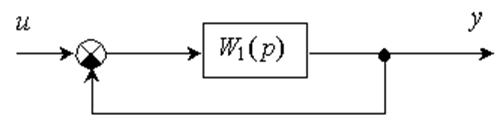
Рисунок 2 – Структурная схема системы управления

Передаточная функция данной системы определяется по формуле

,

.

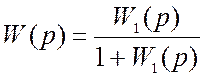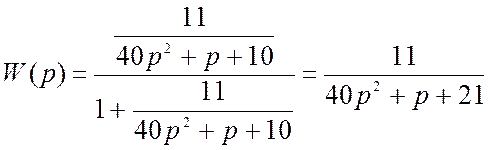Характеристический полином системы имеет вид

.

Для определения полюсов системы решается уравнение (решение см. Приложение А)

.

Полюса системы:

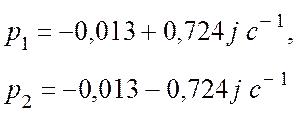
Расположение данных полюсов на комплексной плоскости представлено на рисунке 3.

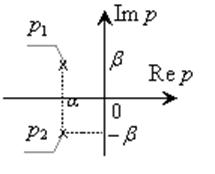
Рисунок 3 – Расположение комплексно-сопряженных полюсов системы

Определение временных характеристик системы

Изображение переходной характеристики определяется:

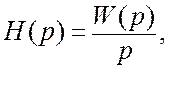
где – передаточная функция системы.

Тогда для данной системы управления

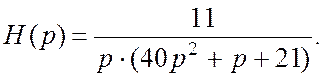
Оригинал переходной характеристики определяется по формуле

,

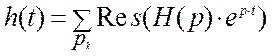где 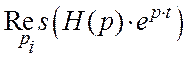– вычет подынтегральной функции,  – полюсы подынтегральной функции.

Таким образом, вычеты определяются:

;

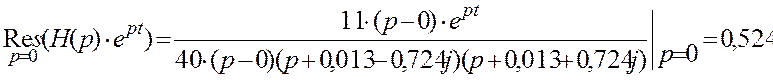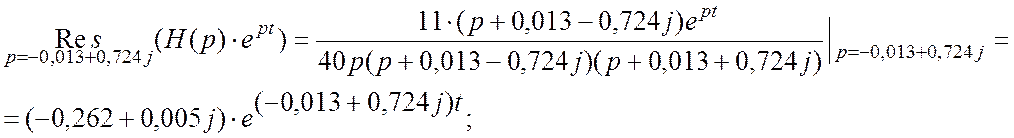
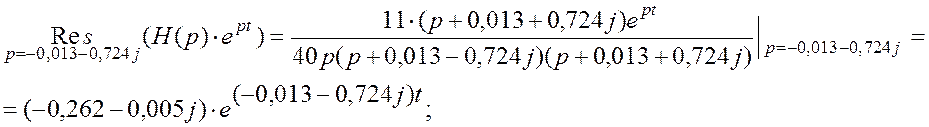
  Оригинал переходной характеристики имеет вид

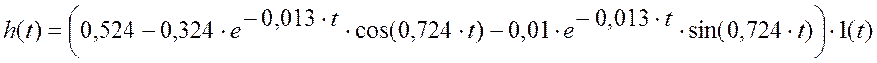,В

График переходной характеристики изображен на рисунке 4

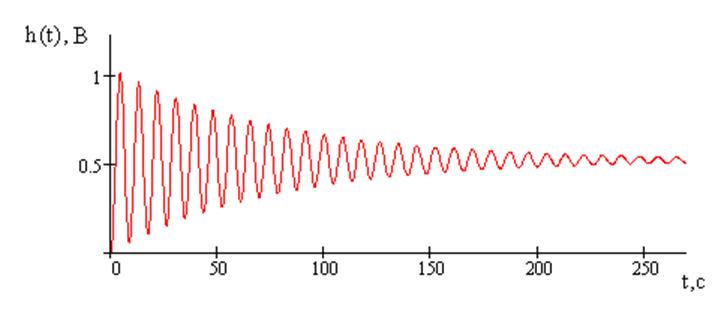
Рисунок 4 – График переходной характеристики

Импульсная характеристика вычисляется путем дифференцирования переходной характеристики

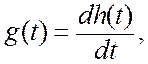
тогда импульсная характеристика имеет вид

,B

График импульсной характеристики изображен на рисунке 5.

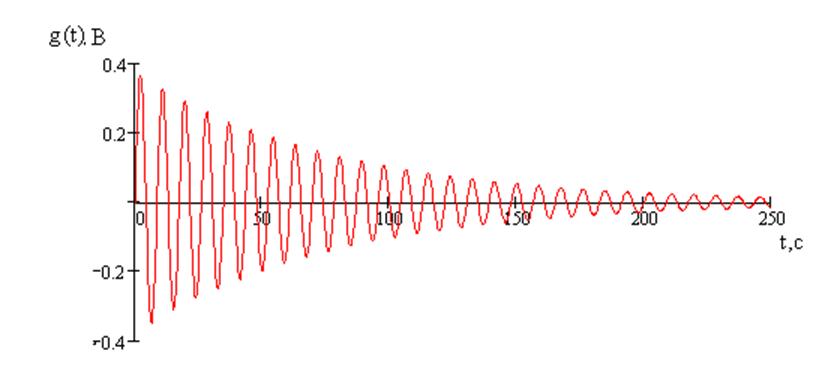
Рисунок 5 – График импульсной характеристики

Определение основных показателей качества переходного процесса по переходной характеристике

По графику переходной характеристики определяют прямые показатели качества.

1) перерегулирование σ – относительное значение первого выброса переходной характеристики, то есть.

,

.

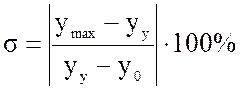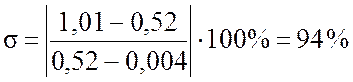2) время переходного процесса t_n – время, после которого выходной процесс не выходит за границы данной области

t_n=250,3 с.

3) статическая ошибка  – это ошибка в установившемся режиме при действии на систему стационарного сигнала.

,

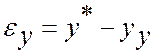где  – входной сигнал,

 – установившееся значение переходного процесса.

Определить и построить частотные характеристики системы управления (АЧХ, ФЧХ, ЛАЧХ, ЛФЧХ, АЛАЧХ)

Передаточная функция системы управления имеет вид

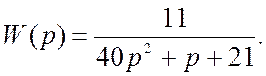
Комплексный коэффициент передачи имеет вид

,

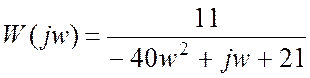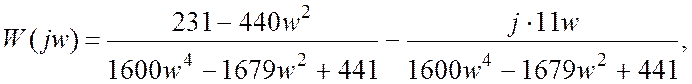
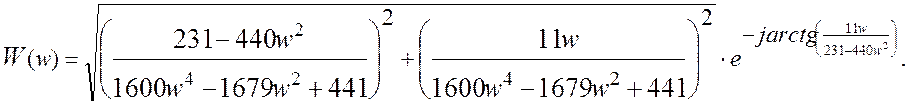
Исходя из полученного выражения, АЧХ и ФЧХ системы будут находиться:

,

.

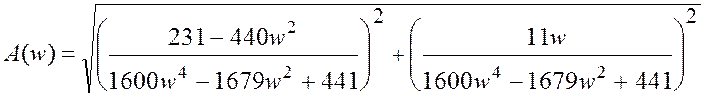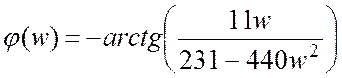Графики АЧХ и ФЧХ изображены на рисунках 6 и 7, соответственно

Рисунок 7 – График АЧХ

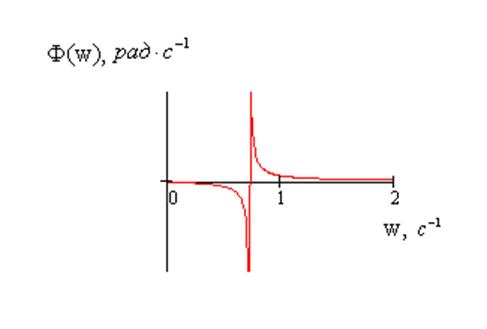
Рисунок 8 – График ФЧХ

ЛАЧХ определяется

,

при построении графика по оси абсцисс откладывается .

График ЛАЧХ  изображен  на рисунке 9.

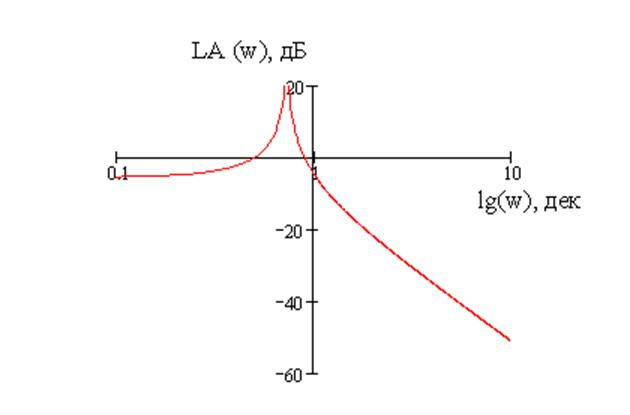
Рисунок 9 – График ЛАЧХ

Построение асимптотической логарифмической амплитудно-частотной характеристики (АЛАЧХ).

Для этого нужно представить передаточную функцию в виде типового звена

Передаточная функция замкнутой системы управления имеет вид:

,

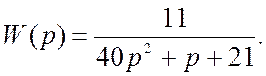тогда преобразованная передаточная функция имеет вид:

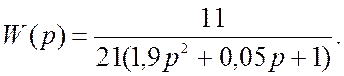
Система представляет собой колебательное звено.

Коэффициент усиления звена .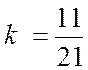

Определение  частоты точки излома. Для этого необходимо найти значение постоянной времени звена:

с,

откуда

с

Тогда значение частоты точки излома будет:

,

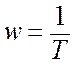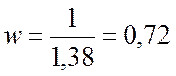рад/с.

Определение точки пересечения низкочастотной асимптоты через коэффициент усиления звена

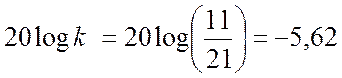Дб.

Колебательное звено дает наклон – 40 дБ/дек.

График АЛАЧХ изображен на рисунке 10.

Определение  полосы пропускания

Определение полосы пропускания представлено на рисунке 11

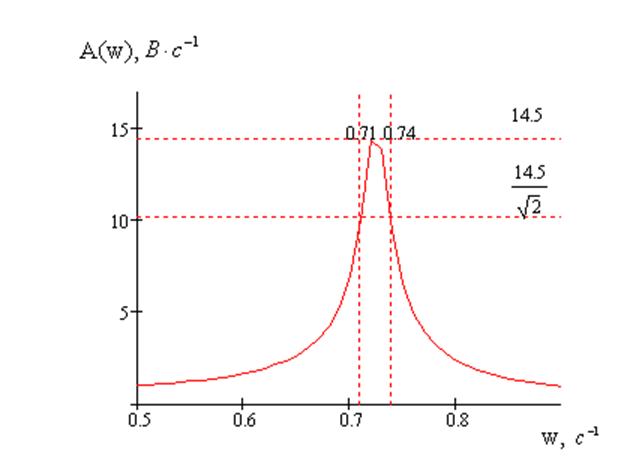
Рисунок 11 – Определение полосы пропускания

–полоса пропускания

Анализ устойчивости системы. Определение запасов устойчивости.

1. Корневой метод

Система имеет следующие полюса:

.

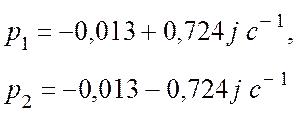Расположение данных полюсов на комплексной плоскости представлено на рисунке 11.

Рисунок 12 – Расположение комплексно-сопряженных полюсов системы

Следовательно, система асимптотически устойчива, т.к. выполняется условие

,

то есть действительные части корней меньше нуля.

2. Метод Рауса-Гурвица

Характеристическое уравнение системы имеет вид

.

Матрица Гурвица составляется из коэффициентов данного уравнения

,

.

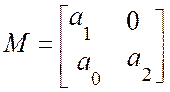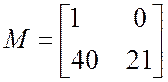следовательно, система устойчива.

3. Критерий устойчивости Михайлова

Характеристический полином системы управления  имеет вид:

.

Характеристический комплекс можно получить путем замены аргумента  чисто мнимой переменной :

.

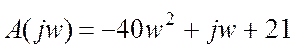Вещественная и мнимая части:

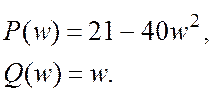
Годограф Михайлова изображен на рисунке 13.

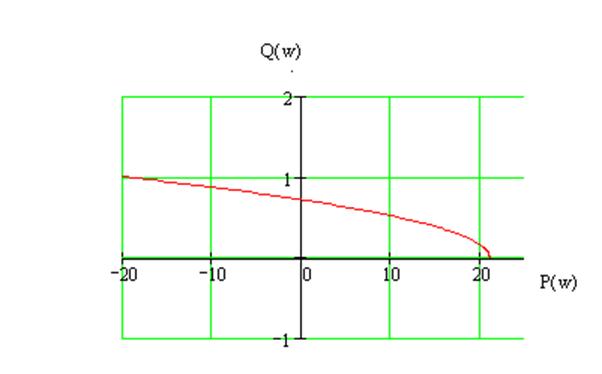
Рисунок 13 – Годограф Михайлова