Критерий Михайлова: Для устойчивости линейной системы (наличия только
полюсов, расположенных в левой полуплоскости) необходимо и достаточно, чтобы
изменение аргумента годографа ее характеристического полинома степени ![]() составляло (
составляло (![]() )
рад или
)
рад или ![]() квадрантов (четвертей) при изменении
частоты
квадрантов (четвертей) при изменении
частоты ![]() .
.
В данном случае ![]() , годограф Михайлова
проходит 2 квадранта, поэтому можно сделать вывод, что система является устойчивой.
, годограф Михайлова
проходит 2 квадранта, поэтому можно сделать вывод, что система является устойчивой.
Критерий Найквиста
Вывод об устойчивости замкнутой системы можно сделать на основе анализа ее частотных характеристик в разомкнутом состоянии.
Передаточная функция разомкнутой системы управления
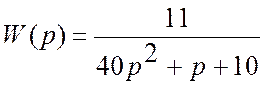 .
.
Комплексный коэффициент передачи имеет вид
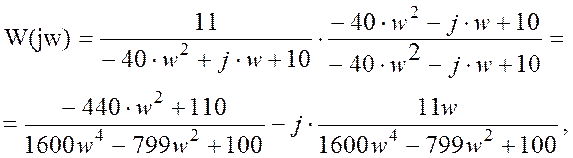
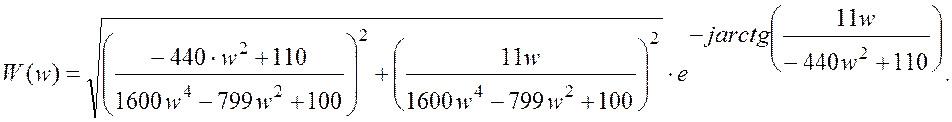
Исходя из полученного выражения, АЧХ и ФЧХ системы будут находиться:
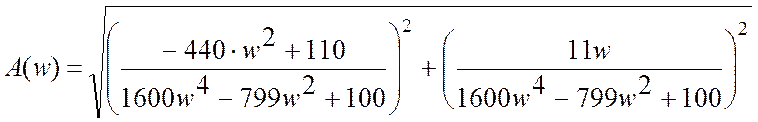 ,
,
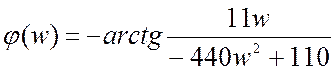 .
.
Графики АЧХ и ФЧХ системы изображены на рисунках 14 и 15, соответственно
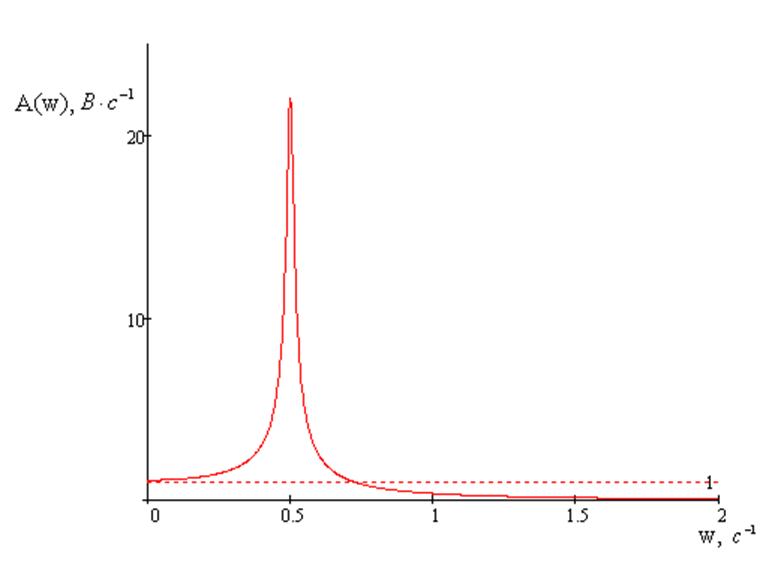
Рисунок 14 – АЧХ
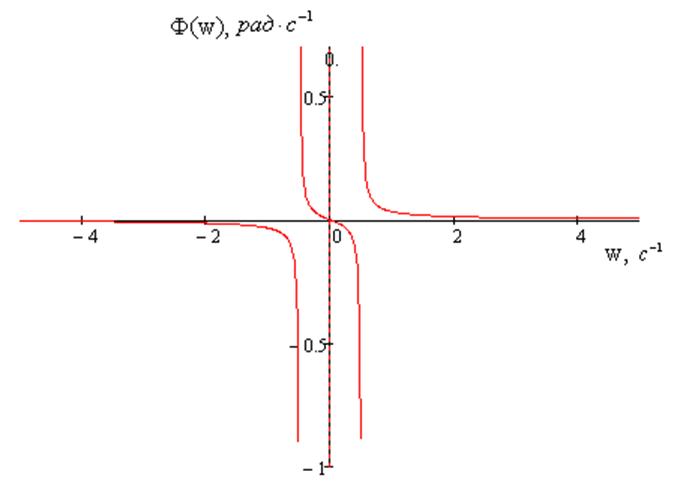
Рисунок 15 – ФЧХ
Система устойчива, так как выполняются необходимые требования.
Определение запасов устойчивости.
Запас устойчивости по амплитуде L3 определяет, во сколько раз можно увеличить коэффициент усиления, чтобы система оставалась устойчивой
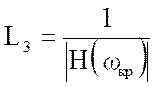 .
.
Определить передаточную функцию последовательного регулятора, который необходимо добавить в прямую связь для коррекции системы РА. В результате чего система должна иметь следующие показатели качества: при подаче ступенчатого воздействия на вход перерегулирование не должно превышать 20 %, время регулирования не более 0,5 с, относительная погрешность регулирования в установившемся режиме не более 0,01 %.
Строится АЛАЧХ разомкнутой системы
Для этого нужно представить передаточную функцию в виде типового звена
Передаточная функция разомкнутой системы управления имеет вид:
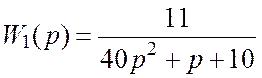 ,
,
тогда преобразованная передаточная функция имеет вид:
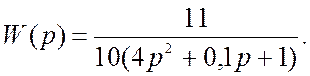
Система представляет собой колебательное звено.
Коэффициент усиления звена 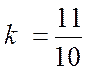 .
.
Определение частоты точки излома. Для этого необходимо найти значение постоянной времени звена:
![]() с,
с,
откуда
![]() с
с
Тогда значение частоты точки излома будет:
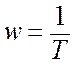 ,
,
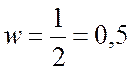 рад/с.
рад/с.
Определение точки пересечения низкочастотной асимптоты через коэффициент усиления звена
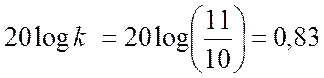 Дб.
Дб.
Колебательное звено дает наклон – 40 дБ/дек.
График АЛАЧХ изображен на рисунке 16.
Построение желаемой асимптотической характеристики (ЖАЛАЧХ)
Порядок
астатизма ![]() .
.
На частоте ![]() рад/с откладывается величина
рад/с откладывается величина ![]() . Через полученную точку проводим
НЧ асимптоту с наклоном минус 20дБ/дек.
. Через полученную точку проводим
НЧ асимптоту с наклоном минус 20дБ/дек.
Определение частоты среза
С помощью номограммы Солодовникова и по заданным показателям качества (время переходного процесса tn ≤ 0,5, перерегулирование σ ≤ 20%) выбирается значение частоты среза, которая влияет на устойчивость системы.
![]() ;
;
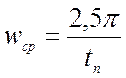 ;
;
![]() =15,7 рад/с .
=15,7 рад/с .
Проводят среднечастотную асимптоту с наклоном минус 20 дБ/дек в диапазоне частот [ωс, ωв], которые выбираются из соотношений
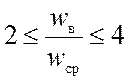 ,
,
![]() ,
,
откуда
31,4 ≤ ![]() ≤
62,8 рад/с .
≤
62,8 рад/с .
Так как
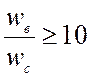 ,
,
и если взять ширину среднечастотного участка 1 дек, то диапазон нижней частоты составит
3,14 ≤ ![]() ≤6,28
рад/c.
≤6,28
рад/c.
Выбираются значения граничных частот среднечастотного участка
![]()
Строят сопрягающую часть для низкочастотной и среднечастотной асимптот с наклоном минус 40 дБ/дек, так как данный наклон облегчает реализацию. Из построения сопрягающей части было определено, что точка пересечения
![]() =0,33 рад/c.
=0,33 рад/c.
Для высокочастотной асимптоты выбирается наклон минус 40 дБ/дек.
Определим передаточную функцию желаемой разомкнутой системы.
Низкочастотная часть имеет наклон минус 20 дБ/дек, что соответствует
интегрирующему звену первого порядка с передаточной функцией ![]() .
.
Сопрягающая часть имеет наклон минус 40 дБ/дек, поэтому описывается
апериодическим звеном первого порядка с передаточной функцией 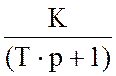 , так как оно дает дополнительный
наклон минус 20 дБ/дек.
, так как оно дает дополнительный
наклон минус 20 дБ/дек.
Среднечастотной части соответствует форсирующее звено с передаточной
функцией ![]() , так как
оно дает дополнительный наклон плюс 20 дБ/дек.
, так как
оно дает дополнительный наклон плюс 20 дБ/дек.
Высокочастотной части соответствует апериодическое звено первого порядка.
Определяется передаточную функцию желаемой разомкнутой системы
Для этого находятся постоянные времени звеньев по соответствующим частотам изломов:
![]()
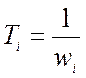 ;
;
![]() =0,33 рад/c,
=0,33 рад/c, ![]() =3,03 с,
=3,03 с,
![]() =4,5 рад/с,
=4,5 рад/с,
![]() =0,282 с,
=0,282 с,
![]() =45 рад/с,
=45 рад/с, ![]() =0,022 с.
=0,022 с.
Таким образом, желаемая передаточная функция разомкнутой системы имеет вид
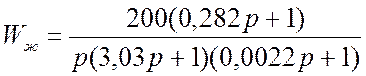
Определение передаточной функции последовательного регулятора
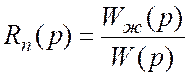 ,
,
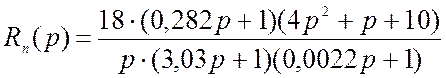 .
.
Анализ скорректированной системы.
Переходная характеристика скорректированной системы представлена на рисунке 17
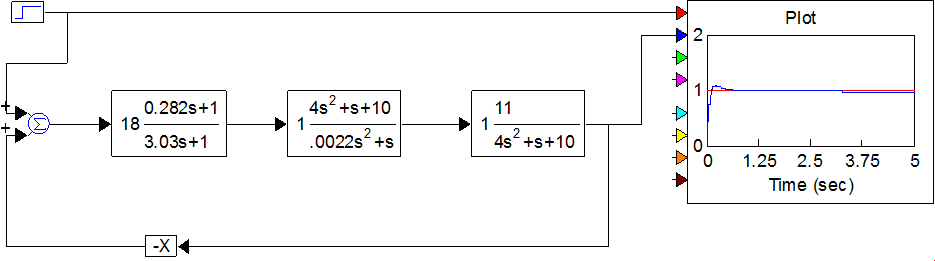
Рисунок 17 – Переходная характеристика скорректированной системы
Определение основных показателей качества представлено на рисунке 18
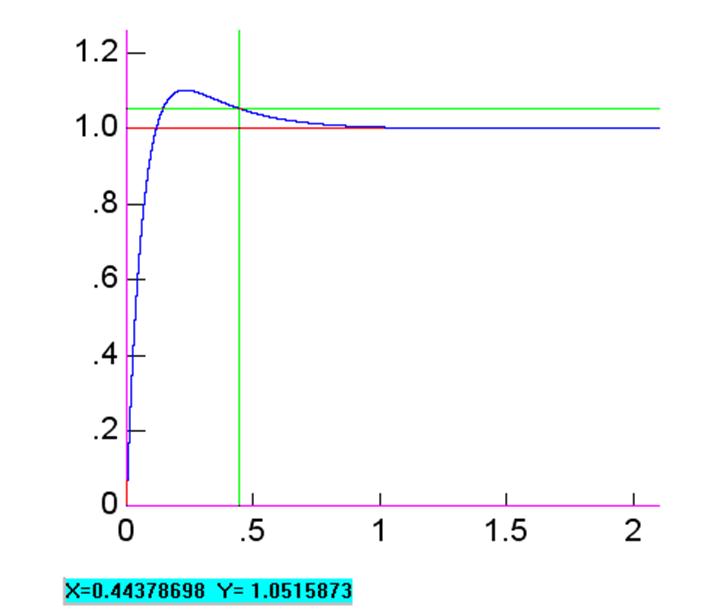
Рисунок 18 – Определение показателей качества
1) перерегулирование σ – относительное значение первого выброса переходной характеристики, то есть.
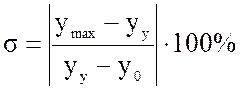 ,
,
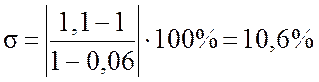 .
.
2) время переходного процесса tn – время, после которого выходной процесс не выходит за границы данной области
tn=0,443 с.
Заключение
В соответствии с заданием были выполнены следующие расчёты:
В задании 1
1) Была найдена передаточная функция системы
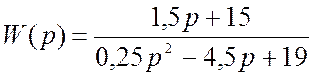 ;
;
2) Записано дифференциальное уравнение, которым описывается система
![]() ;
;
В задании 2
1) Для заданной системы определена передаточная функция и изображены полюсы системы на комплексной плоскости. Получили:
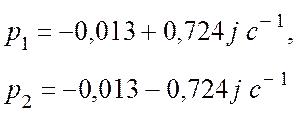
2) Определены и построены переходная характеристика
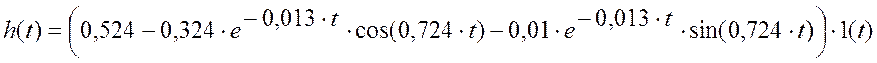 ;
;
импульсная характеристика
![]()
3) Построены АЧХ, ФЧХ, ЛАЧХ, АЛАЧХ системы.
4) Проведен анализ устойчивости системы
5) Определена передаточная функция последовательного регулятора, который необходимо добавить в прямую связь для коррекции системы РА
Литература
1. Баскаков С.И. Радиотехнические цепи и сигналы: Учеб. для вузов по спец. «Радиотехника». – 4-е изд., перераб. и доп. – М.: Высш. шк., 2003. – 405с.
2. Бронштейн И.Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. – 13-е изд., исправленное. – М.: Наука, 1986. – 625с.
3 Лукас В.А. Теория автоматического управления. – 2 изд., перераб. и доп. – М.: Недра, 1990. – 416с.
4.Никулин В.А. Частотные методы анализа и синтеза теории автоматического управления. – 2-е изд., испр. и доп. – М.: Наука, 2000. – 230с.
Приложение А
Нахождение полюсов передаточной функции системы с помощью программы Mahcad
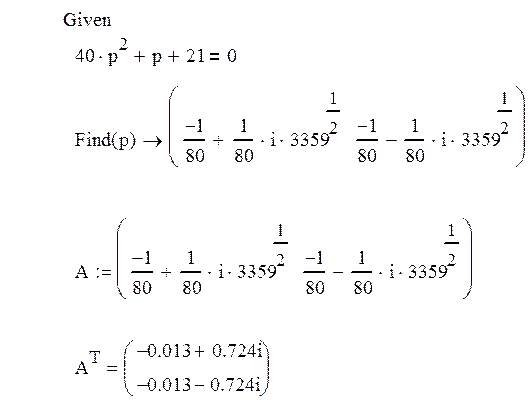
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.