Определение устойчивости системы по критериям устойчивости

Частотный критерий устойчивости Михайлова:

Дана передаточная функция системы:

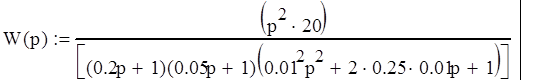
Находим передаточную функцию замкнутой системы:

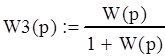
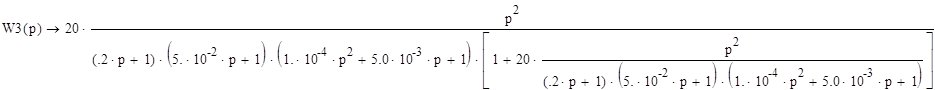
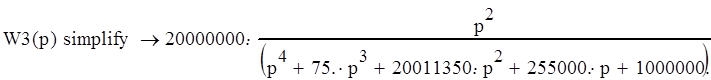
По ней определяем характеристическое уравнение:

В характеристическом уравнении вместо р подставляем :

Находим вещественную и мнимую часть характеристического уравнения:

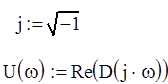
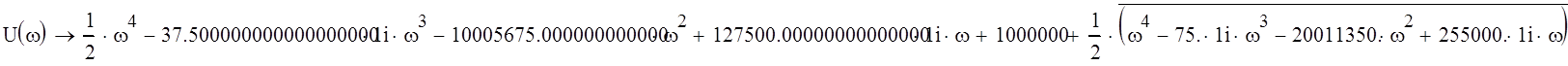
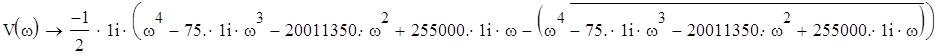
Задаём значение частоты

Строим декартовую систему координат.

Строим годограф михайлова.

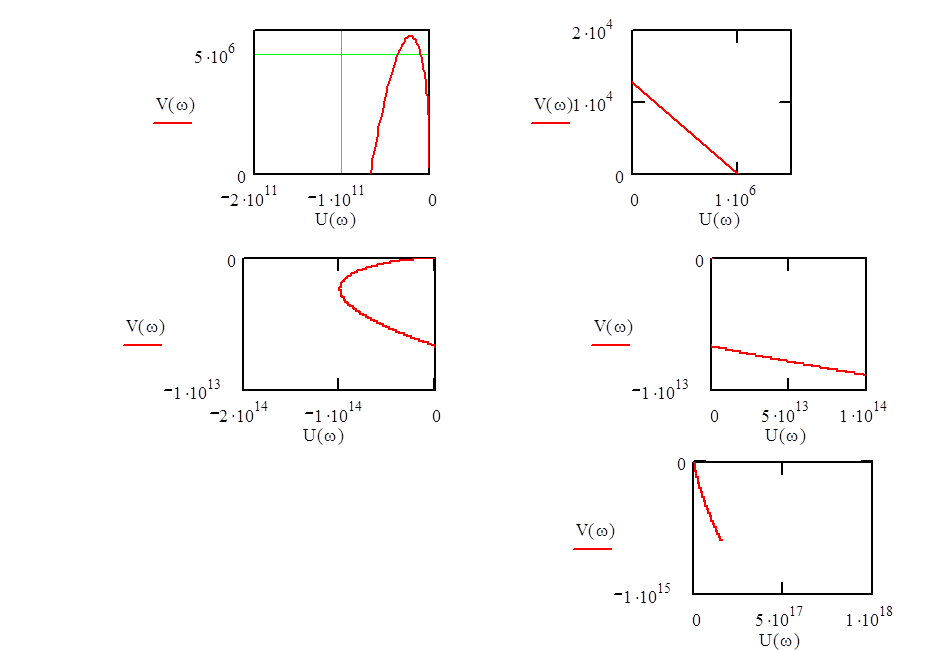
По виду прохождения годографа определяем устойчивость системы:

Проанализировав полученный годограф делаем вывод, что система устойчива, т.к.

1)  Годограф начинается на вещественной оси.

2)  При изменении частоты от 0 до  годограф повернулся против часовой стрелки.

3)  Годограф прошёл четыре квадранта, что совпадает с порядком характеристического уравнения.

4)  Годограф не проходит через начало координат.

                  Критерий устойчивости Гурвица.

Характеристическое уравнение системы имеет вид:

 

Составляем определитель Гурвица:

Определяем диагональные миноры:

      

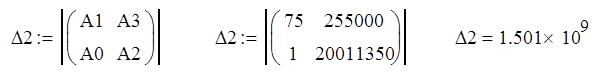
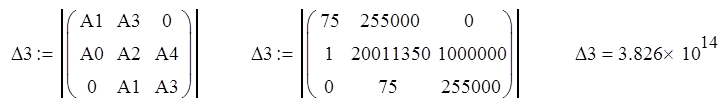
Т.к. главный определитель и его миноры имеют значение больше нуля, то делаем вывод, что система устойчива.

                         Критерий устойчивости Рауса.

Характеристическое уравнение системы имеет вид:

 

Вычисляем третью строку таблицы Рауса.

            

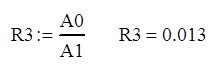
Вычисляем четвёртую строку:

            

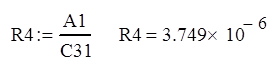
Вычисляем пятую строку:

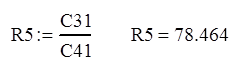
№Строки	R	1Столбец	2Столбец	3Столбец
1		A0=1	A2=20011350	A4=1000000
2		A1=75	A3=255000	A5=0
3
4
5

Т.к. коэффициенты первого столбца положительны, то делаем вывод, что система устойчива.

                  Балаковский Институт Техники Технологии и Управления

                        Лабораторная работа №2

Определение устойчивости системы по критериям устойчивости.

                                                                           Выполнил: студенты гр.УИТ-32в

                                                                                                  Ильин А.В.

                                                                           Проверил: Стельмах И.В.

                                            Балаково 2003г.