Определение временных и частотных характеристик систем автоматического управления в Matlab

Определение временных и частотных

характеристик Систем автоматического

управления в Matlab

Цель работы: получение навыков исследования линейных динамических моделей в программном пакете Matlab и ознакомление с временными и частотными характеристиками систем автоматического управления (САУ).

			b0	b1	b2	a0	a1	a2	а3
2.		1.	0	-3	2	4	2	3	9
		2.	8	0	-3	-4	-6	-4	-1
		3.	-4	6	-2	5	5	0	1
		4.	6	-8	-7	0	-6	-3	-1
		5.	2	-1	-3	-1	0	-7	-2

Вариант № 6

Выберем согласно таблице, приведенной выше и варианту передаточную функцию вида:

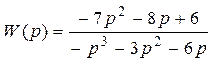
Преобразуем данную передаточную функцию в более удобный вид, домножив числитель и заменатль на -1:

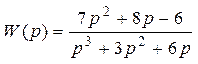
Запишем передаточную функцию в командной строке программы Matlab при помощи функции tf. В итоге программа распознает введенные данные как передаточную функцию w(s):

>> w=tf([7 8 -6],[1 3 6 0])

Transfer function:

      7 s^2 + 8 s - 6

-----------------------

1 s^3 + 3 s^2 + 6 s

Для определения полюсов передаточной функции введем команду pole(w)

>> pole(w)

ans =

  0

  - 1.5000 + 1.9365i

  - 1.5000 - 1.9365i

Из результатов вычисления полюсов функции, отметим, что система находится на границе устойчивости. Это следует из корневого метода определения устойчивости. В данном случае вещественные части отрицательны, но один из корней имеет нулевую вещественную часть и мнимую части, т.е. лежит на мнимой оси.

Для определения нулей передаточной функции, запишем команду zero(w)

>> zero(w)

ans =

  -1.6594

  0.5165

Для построения переходного процесса воспользуемся командой step (w)

>> step (w)

Переходный процесс неустойчивый. Т.е. при подаче на вход системы управления единичной функции Хэвисайда, система никогда не выходит на заданное единичное значение, и продолжает падать. Такой характер падения переходного процесса объясняется наличием интегральной составляющей в передаточной функции:

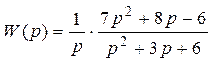
Для построения импульсной характеристики, подадим на вход системы бесконечно большой импульс за бесконечно малое время с помощью команды impulse (w). При подаче такого сигнала, система возвращается в исходное положение.

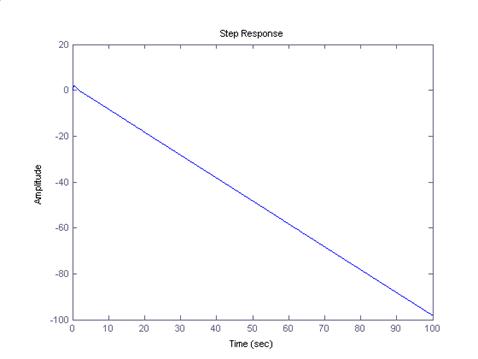
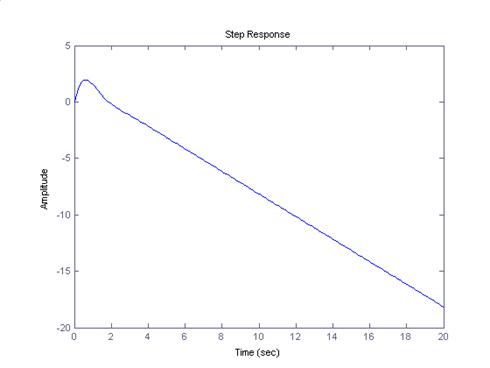
На рисунках видно, что характер падения переходного процесса не изменяется с течением времени

Построим импульсную переходную характеристику:

>>impulse(w)

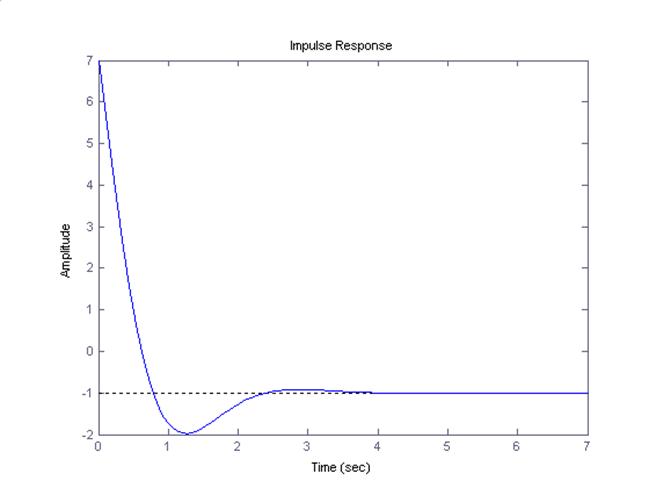
Подадим на вход системы дельта-функцию Дирака. При этом система отработает данное задающее воздействие, но вернется не в нулевое состояние, а в точку -1.

Для построение логарифмической амплитудно-частотной характеристики воспользуемся командой bode(w)

>>bode(w)

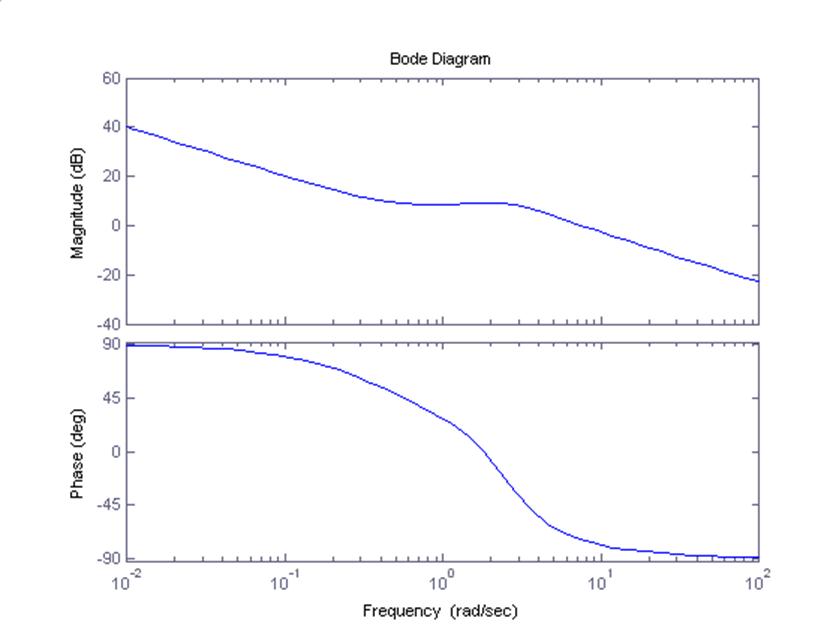
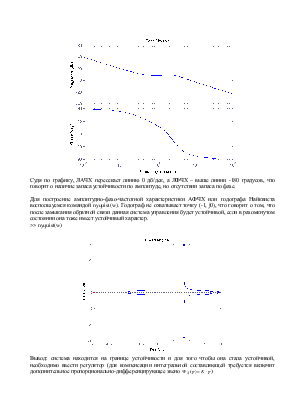
Судя по графику, ЛАЧХ пересекает линию 0 дб/дек, а ЛФЧХ – выше линии -180 градусов, что говорит о наличие запаса устойчивости по амплитуде, но отсутствии запаса по фазе.

Для построение амплитудно-фазо-частотной характеристики АФЧХ или годографа Найквиста воспользуемся командой nyquist(w). Годограф не охватывает точку (-1, j0), что говорит о том, что после замыкания обратной связи данная система управления будет устойчивой, если в разомкнутом состоянии она тоже имеет устойчивый характер.

>> nyquist(w)

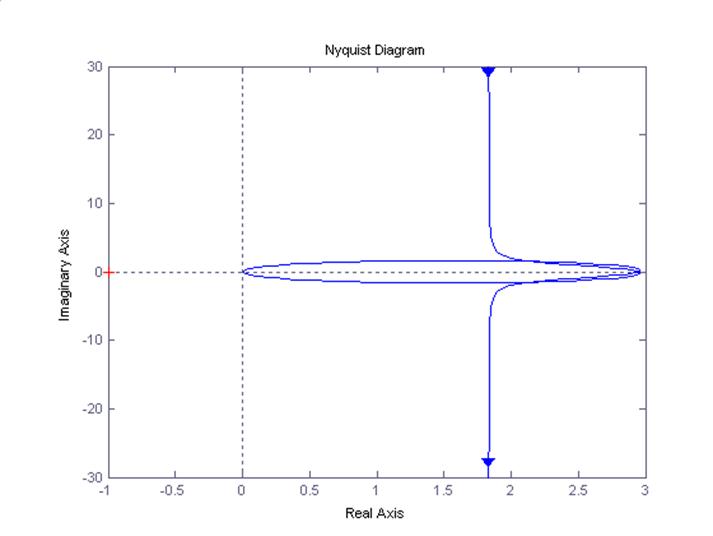
Вывод: система находится на границе устойчивости и для того чтобы она стала устойчивой, необходимо ввести регулятор (для компенсации интегральной составляющей требуется включит дополнительное пропорционально-дифференцирующее звено )