Определение ошибки в системе и её устранение

При

Система астатическая по задающему воздействию (в системе имеется интегратор), статическая относительно возмущения (интегрирующее звено расположено после точки приложения возмущения).

В системе возникает ошибка, которая складывается из ошибки по задающему воздействию и ошибки по возмущению:

     (1)                                                            

Где С_i- коэффициенты ошибок.

+

С₀- статическая ошибка;

С₁- коэффициент скоростной ошибки.

Изображение ошибки определяется по следующей формуле:

    (2)

Где - передаточная функция по ошибке;

- передаточная функция относительно возмущения;

- изображение входного сигнала;

- изображение возмущения.

Передаточная функция замкнутого контура определяется следующим образом:

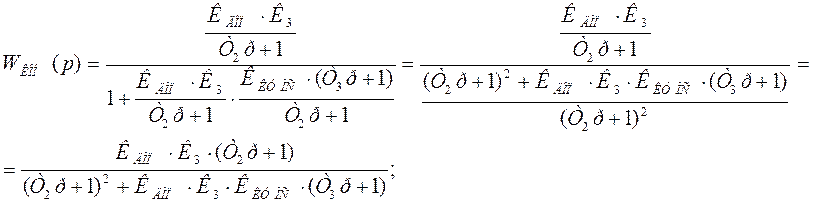
Тогда запишем передаточную функцию скорректированной системы, подставив найденную выше передаточную функцию замкнутого контура:

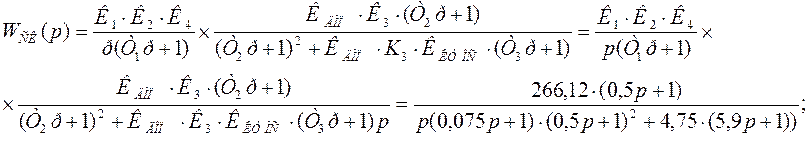
Находим передаточные функции по ошибке и относительно возмущения:

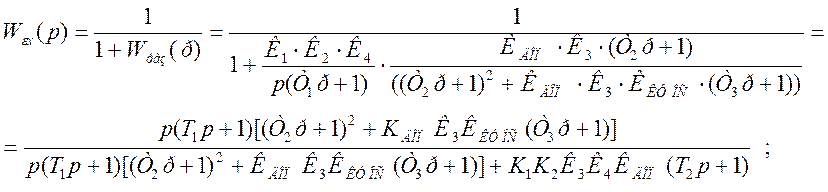
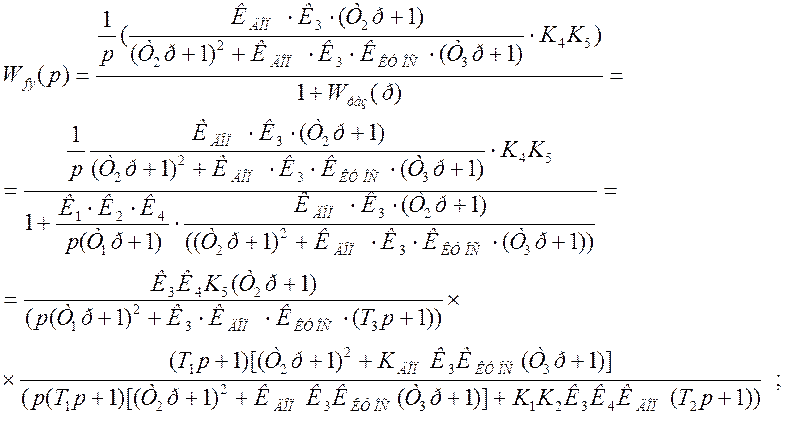
                (3)

; .

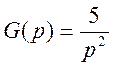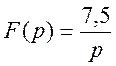Подставляем найденные передаточные функции, изображения входного сигнала и возмущения в формулу (3) и вычисляем значение ошибки.

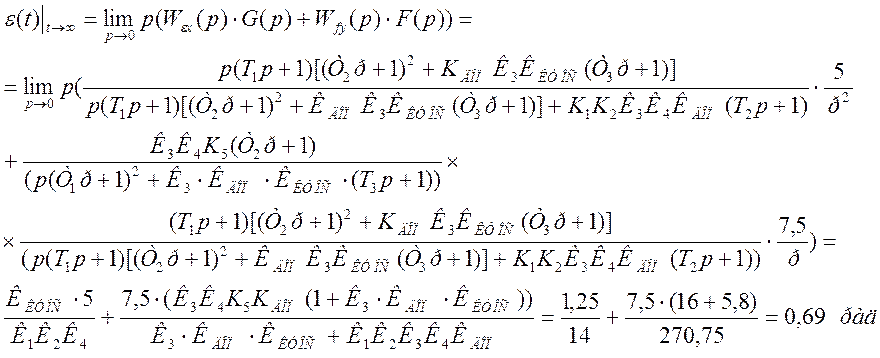
Значение ошибки велико, поэтому для ее уменьшения используем  специальные методы из теории инвариантности (независимость выходного сигнала то изменения задающего воздействия и возмущения).

В данном случае используем инвариантность относительно возмущения, поскольку составляющая часть ошибки по возмущению большая.

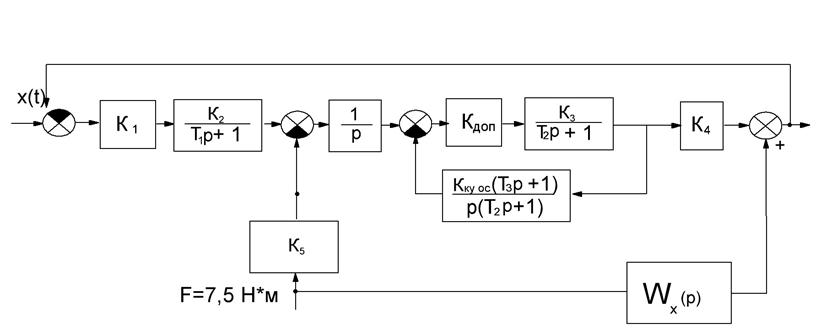
Для обеспечения инвариантности вводим второй канал передачи возмущения. Тогда система будет иметь следующую структуру:

	Рисунок 3.-Структурная схема с добавлением второго канала передачи возмущения

 

Чтобы выходная переменная не зависела от возмущения, надо чтобы передаточная функция, связывающая возмущение и выход была равна нулю=0.

Запишем передаточную функцию, связывающую возмущение и выход, и приравняем ее к нулю:

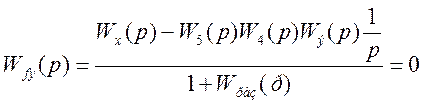, где - передаточная функция замкнутого контура.

, ,

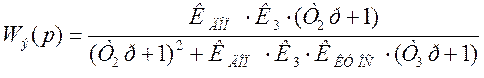
Дробь равна нулю, когда числитель равен нулю:

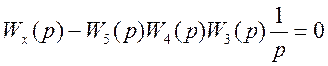
Тогда

.

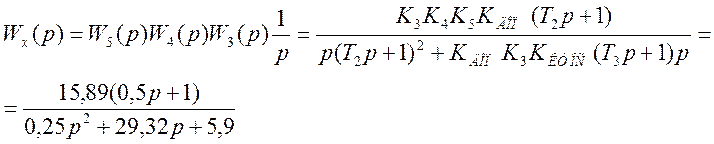Если это условие выполняется, то инвариантность будет обеспечена.