Моделирование систем на микро- и макроуровне: Методические указания к выполнению курсового проекта

Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт, техники, технологии и управления

МОДЕЛИРОВАНИЕ СИСТЕМ НА МИКРО- И МАКРОУРОВНЕ

Методические указания к выполнению курсового проекта

по дисциплине «Моделирование систем» для студентов специальности 210100 вечерней формы обучения

Одобрено

редакционно-издательским советом

Балаковского  института техники,

технологии и управления

Балаково 2009

Курсовой проект включает в себя решение следующих задач:

- овладение навыками расчетов согласно теории систем с распределенными параметрами;

- знакомство с уравнениями и специальными функциями математической физики;

- формирование математической модели гидравлической системы в динамическом и статическом режиме;

- использование при этом различных форм представления моделей: графической, матричной, в виде системы дифференциальных уравнений в нормальной форме Коши и линейных уравнений;

- анализ полученной динамической модели качественным способом для определения ее устойчивости;

- решение статической модели системы численным методом.

УКАЗАНИЯ ПО СОСТАВЛЕНИЮ И ОФОРМЛЕНИЮ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ

В расчетно-пояснительной записке даются подробные данные к работе и отражают все пункты задания на курсовую работу. Рекомендуется следующее содержание расчетно-пояснительной записки:

1  Моделирование на микроуровне.

1.1  Основные понятия СРП

1.2  Выбор и идентификация уравнения

-  уравнение со всеми данными, тип уравнения, вид граничных и начальных условий;

-  задание выходного параметра Q, входной величины f (единица измерения, функция, например, f(x,y,t)=sin(2t), обоснование выбора), выверка размерностей;

-  задание начальных и граничных условий, обоснование выбора;

-  упрощенная запись стандартизирующей функции (при необходимости)

1.3  Расчет выходной величины

-  запись и вычисления двойного интеграла по времени и пространственной области от произведения функции Грина на стандартизирующую функцию. Интеграл по пространственной области будем двойным для двумерной задачи, тройным для трехмерной, таким образом, с учетом интеграла по времени:

одномерная задача – двойной интеграл,

двумерная задача – тройной интеграл,

трехмерная задача – четверной интеграл.

-  Отследить, что при подстановке стандартизирующей функции, необходимо поменять переменные с выходных на входные.

-  После нахождения выходной величины задается фиксированное время, при котором процесс можно считать установившемся (например t=10) и строится статическая характеристика. Для одномерной задачи зависимость выходной величины от координаты х, для двумерной задачи – поверхность (зависимость Q от x,y), для трехмерной задачи – поверхность при фиксированном значении третьей координаты.

1.4  Расчет интегральной передаточной функции.

- Если по заданию неизвестная континуальная передаточная функция, то она находится следующим образом:

.

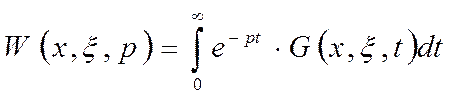-  находится преобразование Лапласа от стандартизирующей функции,  и выделяется из него входное воздействие. Остаток после выноса входного воздействия участвует в дальнейшем расчете.

-  находится интегральная ПФ как интеграл по пространственной области от произведения континуальной ПФ на остаток стандартизирующей функции, найденной ранее. Количество интегралов равно размерности задачи. Аналогично предыдущему пункту в стандартизирующую функцию подставляются входные переменные.

1.5  Построение логарифмических характеристик, синтез аппроксимированной передаточной функции.

-  В найденной интегральной передаточной функции задаются координаты пространственной области (например, средней точки пространственной области или нулевой). Таким образом, получаем интегральную ПФ, зависящую только от оператора дифференцирования р.

-  Строится ЛАЧХ и ЛФЧХ

-  Апроксимируется ЛАЧХ стандартными типовыми наклонами, после чего записывается упрощенная передаточная функция.

2.  Моделирование на макроуровне

2.1   Исходные данные                                                                                    

2.2   Графические формы математической модели гидросистемы              

2.3   Матричные формы математической модели                                        

2.4   Узловой метод формирования математической модели                     

2.5   Расчёт параметров элементов гидросистемы                                        

2.6   Расчёт статической модели гидросистемы                                           

2.7   Анализ динамических свойств гидросистемы                                     

Заключение                                                                                                       

Список использованных источников                                                            

Приложение А                                                                                                 

УКАЗАНИЯ ПО ОФОРМЛЕНИЮ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ

Пояснительная записка должна быть выполнена на листах формата А4, с большим штампом на первом листе и малыми на последующих в соответствии со следующими требованиями.

1) Оформление основного текста:

- Формат шрифта - Times New Roman,

- Размер шрифта – 14;

- Интервал полуторный;

- Выравнивание – по ширине;

- Отступ – 1,25.

2) Оформление заголовков:

- Заголовки разделов печатаются заглавными буквами, номер раздела без точки, выравнивание по ширине с отступом 1,25. Каждый раздел начинается с нового листа.

- Содержание, введение, заключение, список используемых источников заглавными буквами по центру.

- Заголовки подпунктов выполняется строчными буквами. Точка ставится только после указания раздела, к которому относится подпункт. Заголовок подпункта в тексте выделяется пробелами. Исключение составляет, когда подпункт идет сразу после наименования раздела.

- После всех заголовков точка не ставится.