3) Оформление таблиц: таблицы необходимо сопровождать тематическими заголовками, иметь свой номер со сквозной нумерацией.
4) Рисунки должны иметь сквозную нумерацию с тематическим заголовком.
5) Оформление Приложения с графической частью согласно приложениям данного методического указания.
ПРИМЕР МОДЕЛИРОВАНИЯ НА МИКРОУРОВНЕ
1.1 Исходные данные
Исходные данные для выполнения первой части курсового проекта:1) Уравнение колебания струны /4/; с. 84:
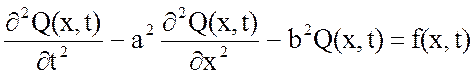 (1)
(1)
2) Начальные условия:
![]() ,
, 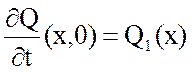
3) Граничные условия:
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
4) Стандартизирующая функция:
![]()
![]() (2)
(2)
5) Функция Грина:
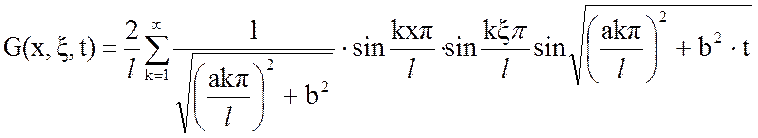 (3)
(3)
6) Континуальная передаточная функция:
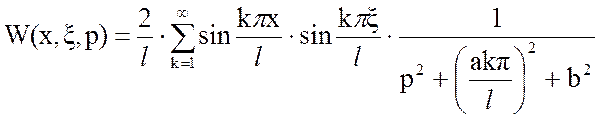 (4)
(4)
1.2 Идентификация краевой задачи
Уравнение (1) представляет собой одномерное уравнение гиперболического типа, имеющую вторую производную по времени t. Данное уравнение описывает колебания струны. Проведём идентификацию всех величин входящих в уравнение (1).
Дифференциальное уравнение имеет вид:
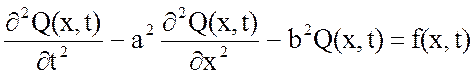 ,
,
где Q(x,t) – выходная распределённая величина, представляющая собой ортогональную деформацию струны, м;
f(x,t) – входное распределённое воздействие на струну, м/c2.
Для уравнения (1) формулируются следующие условия:
- начальные условия: ![]() ,
,
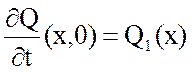 ;
;
- граничные условия: ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Стандартизирующая функция, компенсирующая влияние начальных и граничных условий для данной одномерной задачи имеет вид (2).
Функция Грина, являющаяся решением краевой задачи при начальных и граничных условиях и входном воздействии в виде δ-функции имеет вид (3).
Континуальная передаточная функция, являющаяся преобразованием Лапласа функции Грина имеет вид (4).
Для решения частной задачи примем следующие условия:
- входное воздействие:
f(x,t)=0;
- начальные условия, описывающие положение струны в начальный момент времени:
![]() ,
,
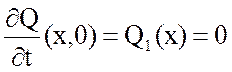 ;
;
- граничные условия, описывающие колебание струны на концах стержня:
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Примем,
что а=1 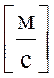 , b=1
, b=1 ![]() , l=2 [м] – длина струны.
, l=2 [м] – длина струны.
Представим на рисунке 1 изображение струны в начальный момент времени:
![]()
![]()
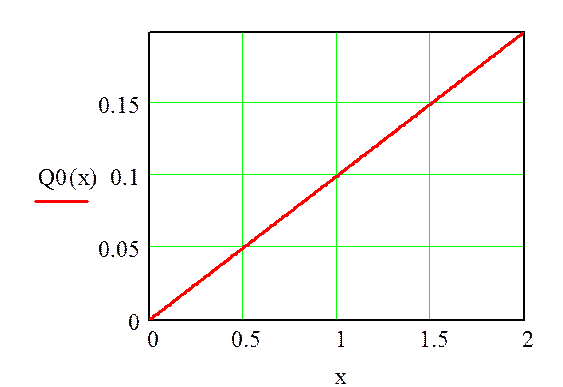
Рисунок 1 – Изображение струны
Отобразим на рисунке 2 граничное условие на конце струны.
Произведём проверку размерности. Пусть Q(x,t) – ортогональное отклонение струны [м]. Тогда входное воздействие f(x,t) имеет размерность [м/с2]:
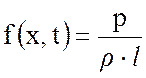 ,
,
где р – давление на струну, Н/м2;
ρ – плотность материала струны, кг/м3;
l – длина струны, м.
Тогда:
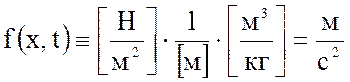
![]()
![]()
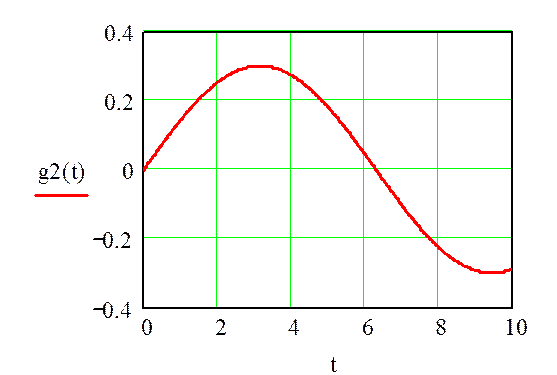
Рисунок 2 – Граничное условие на конце струны
Волновая скорость струны а имеет размерность [м/с]:
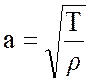 ,
,
где T – натяжение струны, Н/м2;
ρ – плотность материала струны, кг/м3.
Тогда:
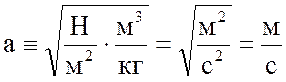
Частота колебания струны b имеет размерность [1/с]:
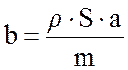 ,
,
где m – масса струны, кг.
Тогда:
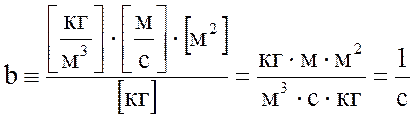
Учитывая размерности всех коэффициентов и величин, входящих в данное уравнение, получим:
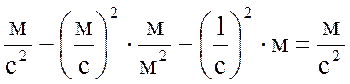 ,
,
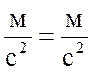 .
.
Размерность соблюдается, следовательно, все коэффициенты подобраны – верно.
С учётом входного воздействия, принятых начальных и граничных условий стандартизирующая функция принимает вид:
![]() ,
,
где δ'(t) и δ'(2-х) – импульсные переменные функции.
1.3 Расчёт статической характеристики
Идентификация исходного уравнения позволяет перейти к расчету распределенной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная композиция от произведения функции Грина на стандартизирующую функцию:
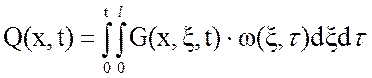 (5)
(5)
Выходная величина Q(x,t) находится как сумма двух составляющих:
Q(x,t)=Q1(x,t) + Q2(x,t), (6)
где Q1(x,t) и Q2(x,t) – первая и вторая составляющие выходной величины и находятся как:
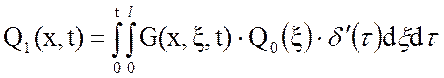 (7)
(7)
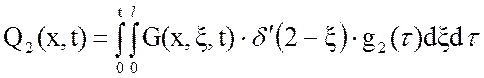 (8)
(8)
Первая составляющая решения выходной функции:
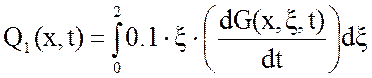 (9)
(9)
Определим производную от функции Грина:
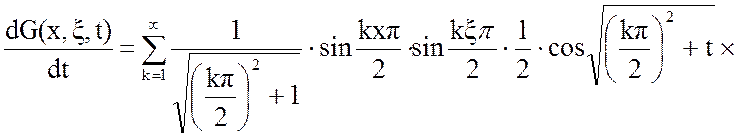
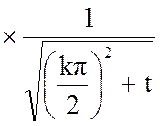 (10)
(10)
Подставим уравнение (10) в (9):
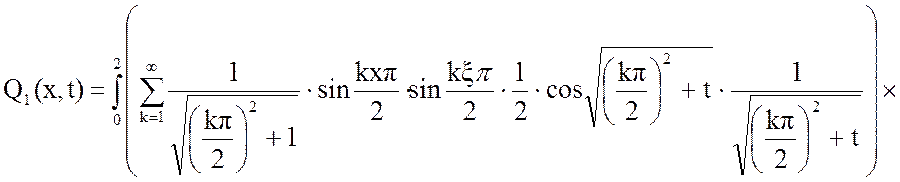
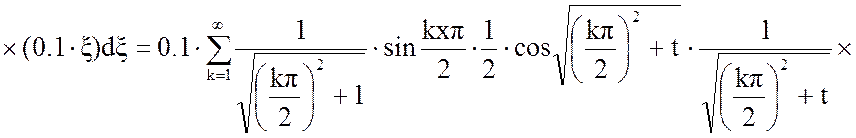
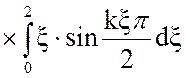
Решим отдельно интеграл:
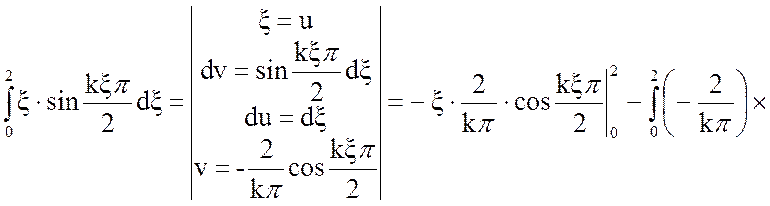
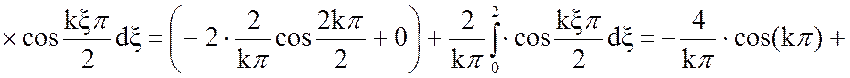
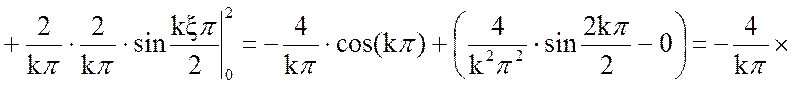
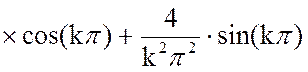 (11)
(11)
Результат расчета:
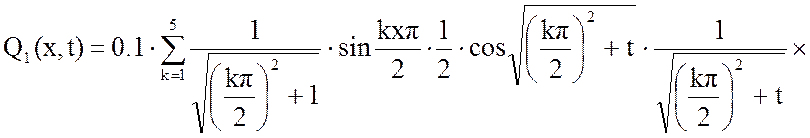
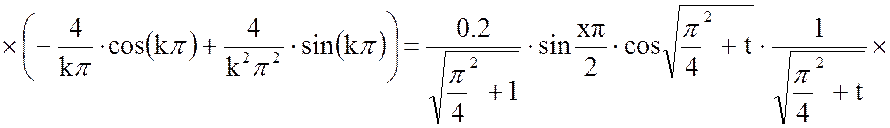
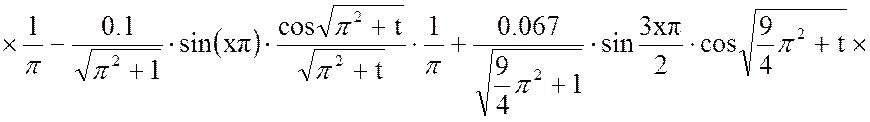
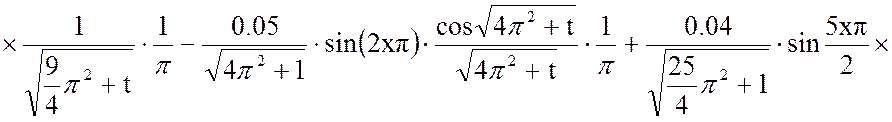
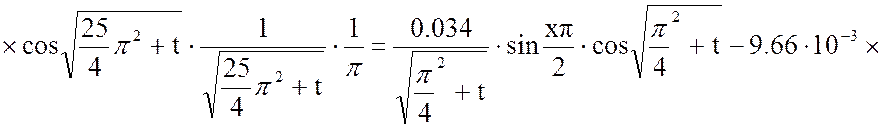
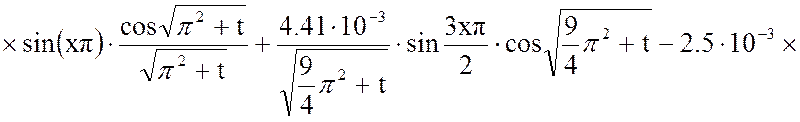
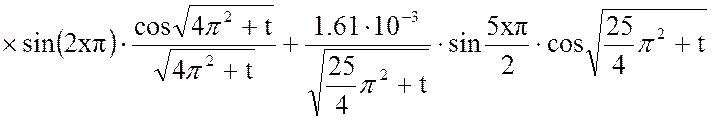
Вторая составляющая решения выходной функции:
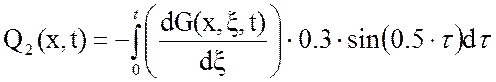 (12)
(12)
Определим производную функции Грина:
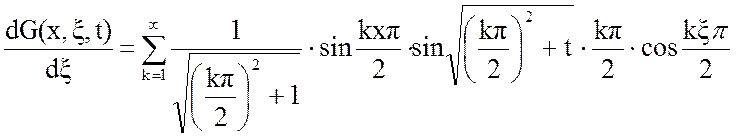 (13)
(13)
Подставим уравнение (13) в (12):
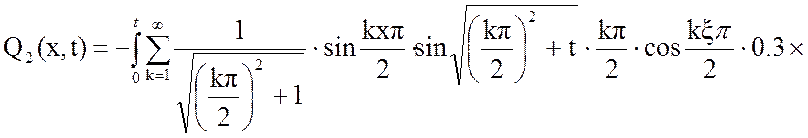
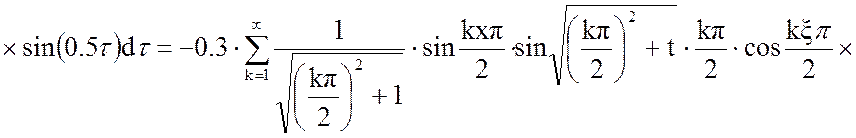
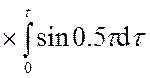
Решим отдельно интеграл:
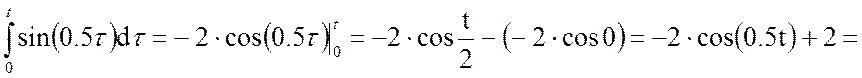
![]()
Пусть ξ=2, тогда:
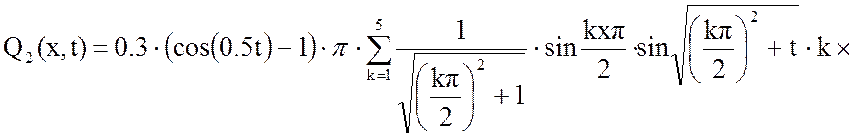
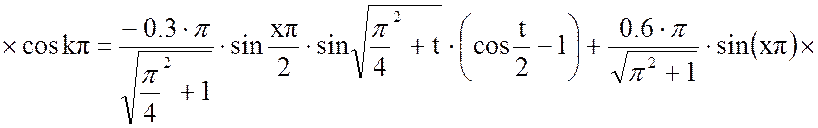
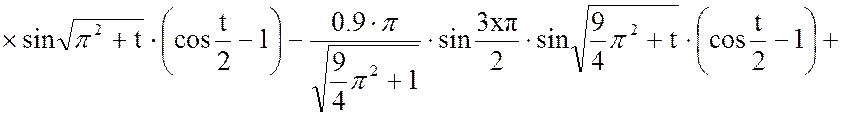
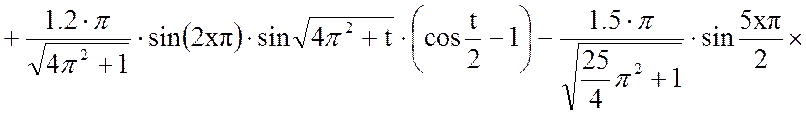
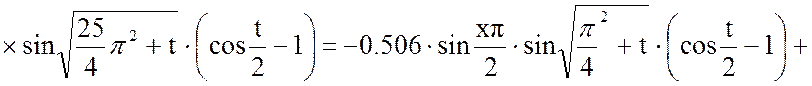
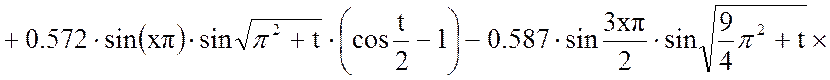
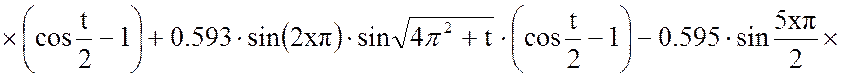
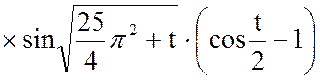
Выходная величина:
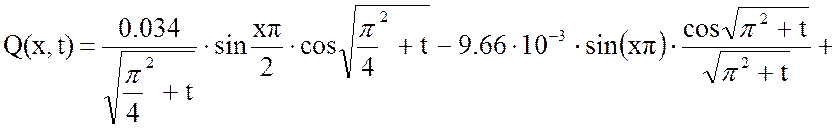
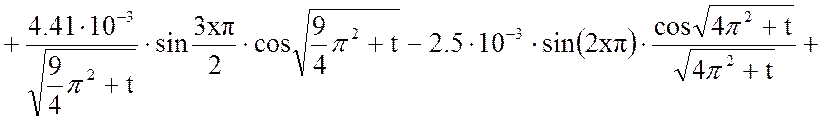
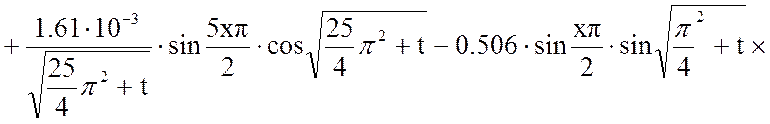
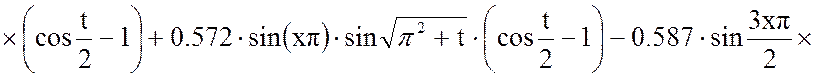
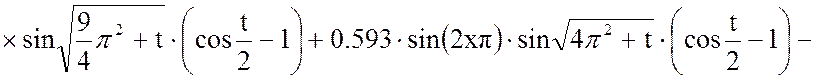
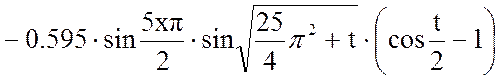
Построим график этой функции при фиксированном времени t.
![]()
![]()
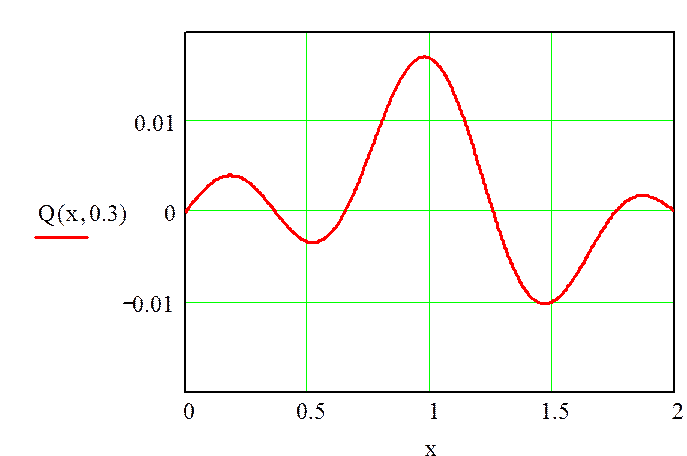
Рисунок 3 – График выходной величины Q(x,t) при t=0.3с
![]()
![]()
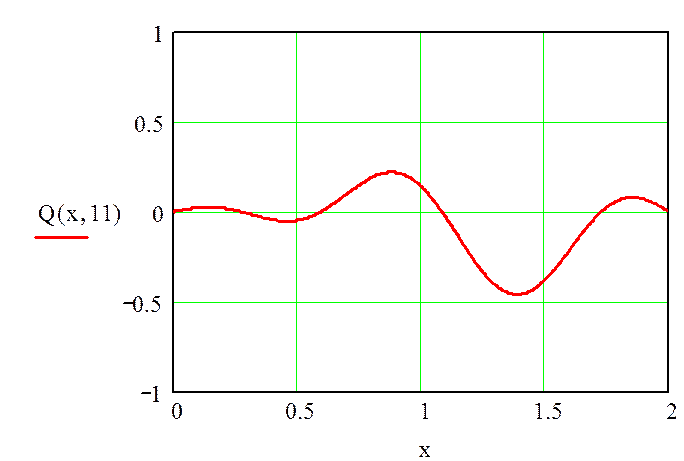
Рисунок 4 – График выходной величины Q(x,t) при t=11с
1.4 Расчёт динамической характеристики
Динамическая
характеристика находится по интегральной передаточной функции 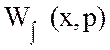 , которая рассчитывается как
пространственная композиция от произведения континуальной передаточной функции
, которая рассчитывается как
пространственная композиция от произведения континуальной передаточной функции ![]() на преобразованную по Лапласу
стандартизирующую функцию
на преобразованную по Лапласу
стандартизирующую функцию ![]() с выделенным из
неё входным воздействием. Так как стандартизирующая функция не содержит входное
воздействие f(x,t), то:
с выделенным из
неё входным воздействием. Так как стандартизирующая функция не содержит входное
воздействие f(x,t), то:
![]() (14)
(14)
Произведём преобразование Лапласа стандартизирующей функции (14):
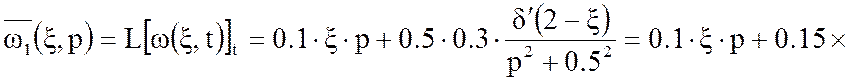
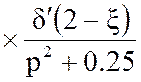
Интегральная передаточная функция:
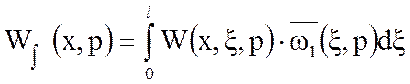 ;
(15)
;
(15)
Подставим данные вариантом значения в уравнение (4):
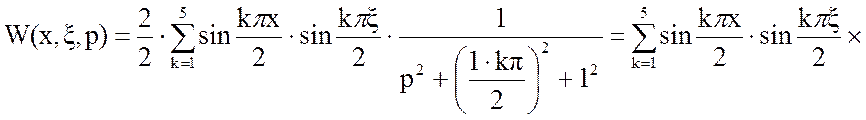
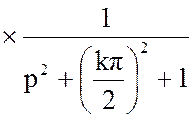
Интегральную передаточную функцию представим в виде:
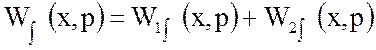 (16)
(16)
Слагаемые ![]() и
и ![]() найдем как:
найдем как:
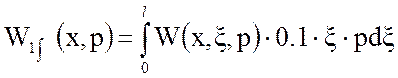 (17)
(17)
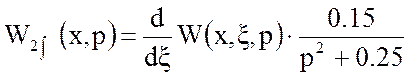 (18)
(18)
Решим первое слагаемое интегральной передаточной функции:
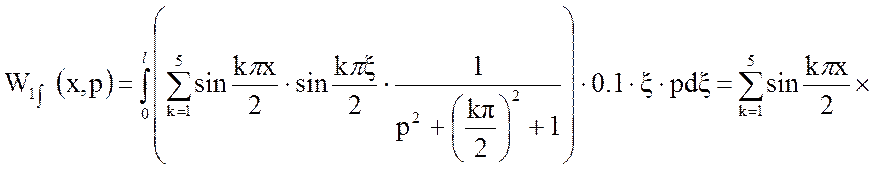
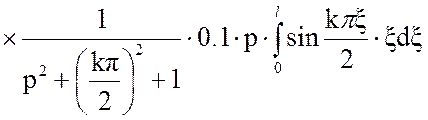 (19)
(19)
Подставим в уравнение (19) уравнение (11) с решённым интегралом, получим:
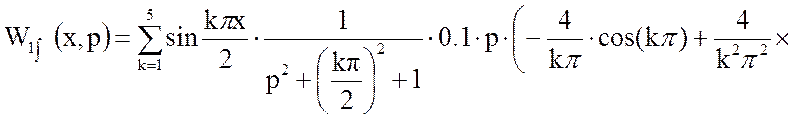
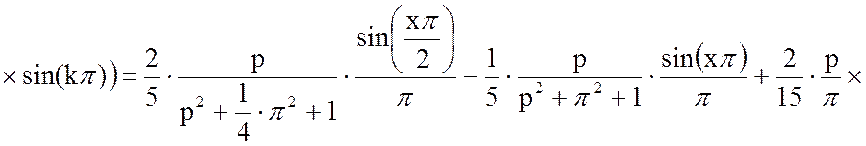
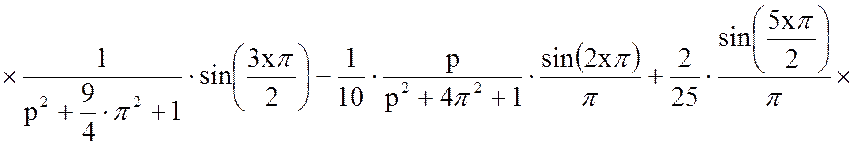
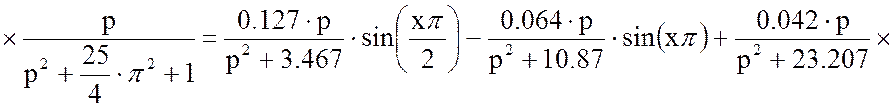
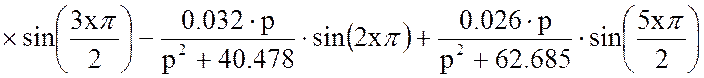
Решим отдельно производную континуальной передаточной функции в уравнении (18):
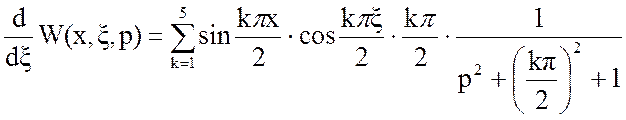
Пусть ξ=2, тогда:
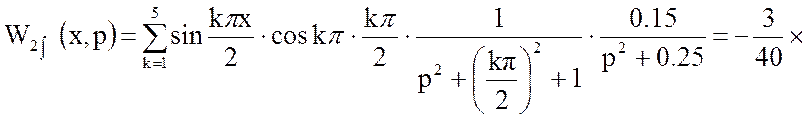
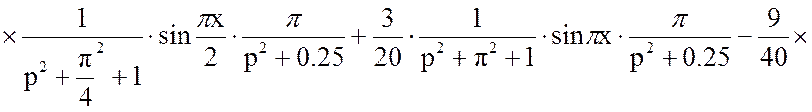
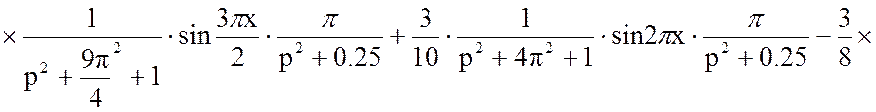
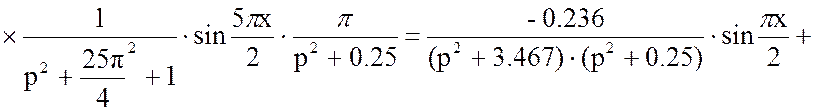
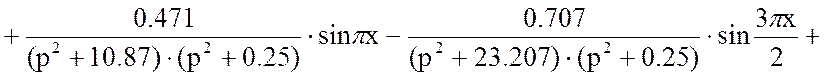
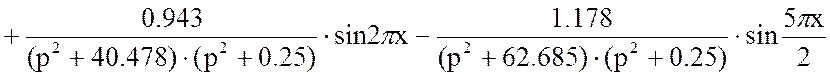
Подставим в уравнение (16) решённые слагаемые ![]() и
и ![]() :
:
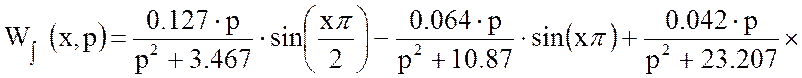
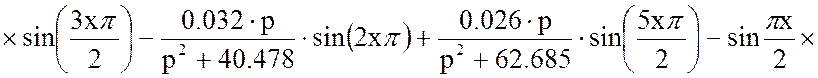
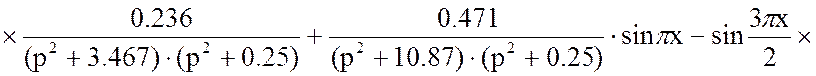
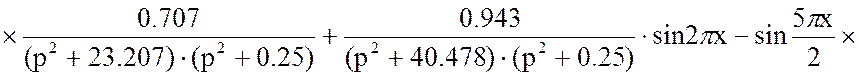
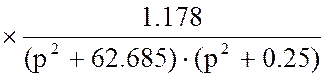 (20)
(20)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.