Другие предметы \ Моделирование систем управления

Моделирование систем на микро- и макроуровне: Методические указания к выполнению курсового проекта, страница 3

Для получения частной передаточной функции в уравнении (20) заменим p на jω, воспользовавшись программой MathCad 11, при х=1, получим:

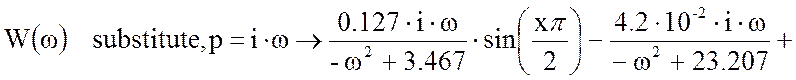
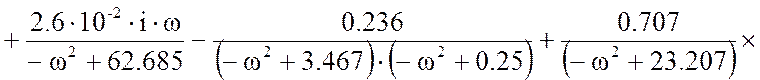
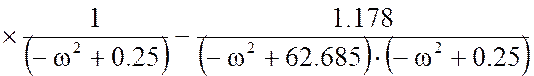
Найдем  ЛАЧХ по выражению:

На рисунке 5 представим ЛАЧХ, построенную в программе MathCad 11. Аппроксимируя полученную ЛАЧХ её стандартными типовыми накло­нами получаем 0 дб/дек и -20 дб/дек, что соответствует апериодическому звену первого порядка. Тогда передаточная функция будет иметь вид:

,

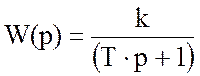где       Т - период, с;

k - коэффициента передачи.

ω1
 

-20 дБ/дек
 

0 дБ/дек
 

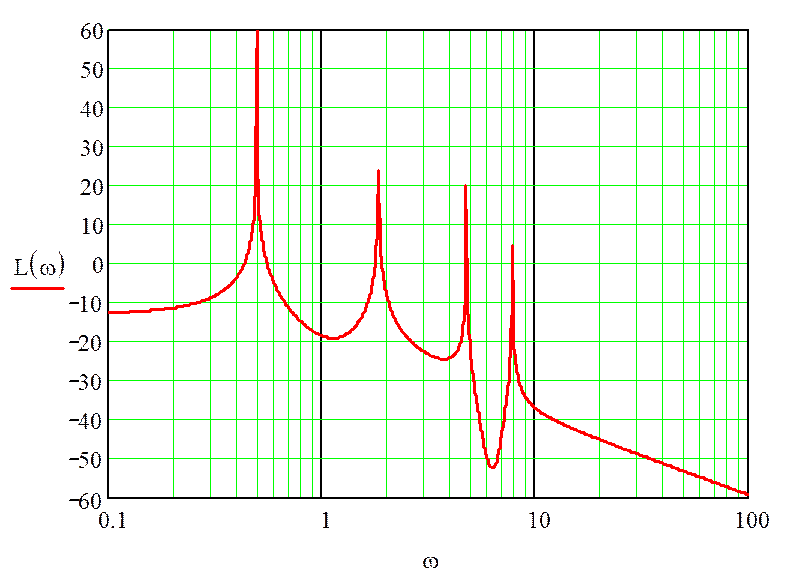
Рисунок 5 – График логарифмической амплитудно-частотной характеристики

Найдем Т при условии, что:

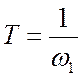
где       ω1 - частота аппроксимированной ЛАЧХ, Гц.

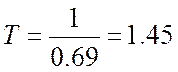 [с]

График ЛАЧХ пересекает ось Y в точке -12.5. Определим значение коэффициента передачи k:

20∙lgk = -12.5, ,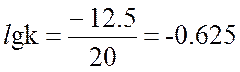

С помощью аппроксимации функция запишется в виде:

.

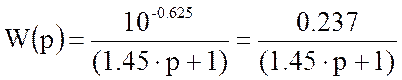ВАРИАНТЫ ЗАДАНИЙ

Таблица 1 - Варианты заданий 1 части курсового проекта

№

Уравнение

Входное воздействие

Начальные условия

Граничные условия

Одномерное параболическое уравнение

1

с.51, нижнее

;   

2

с.51, нижнее

3

с.62, нижнее

4

с.62, нижнее

5

c.64, нижнее

6

c.64, нижнее

7

c.66, нижнее

8

c.66, нижнее

9

c.69, нижнее

*

Одномерное гиперболическое уравнение

10

с.80, нижнее

11

с.80, нижнее

12

с.81

13

с.81

14

с.82, верхнее

15

с.82, верхнее

16

с.82, нижнее *

17

с.83, нижнее

18

с.83, нижнее

19

с.84, нижнее

20

с.84, нижнее

21

с.85, нижнее *

22

с.101, верхнее

23

с.101, верхнее

Двумерное гиперболическое уравнение

24

с.138, нижнее

;

;

25

с.139, нижнее

26

с.141

;

ЛИТЕРАТУРА

1. Тарасик В.П. Математическое моделирование технических систем: учебник для вузов / В.П.Тарасик. –  Мн.: ДизайнПРО, 2004. – 640с.: ил.

2. Бутковский А.Г. Характеристики систем с распределенными параметрами.– М.: Наука, 1979. – 224 с.

ПРИЛОЖЕНИЯ

1) Пример оформления листа перед графической частью с примерным наименованием плакатов.

ПРИЛОЖЕНИЕ А

(обязательное)

Графическая часть

1 Исходные данные и идентификация краевой задачи                             41

2 Расчёт статической характеристики                                                        42

3 Расчёт динамической характеристики                                                    43

4 Моделирование струны в среде ELCUT 5.2                                            44

5 Моделирование на макроуровне. Исходные данные                             45     

6 Графические формы математической модели                                         46

7 Расчет статического режима гидросистемы                                            47

8 Расчет динамического режима гидросистемы                                         48

2) ПРИМЕРНЫЙ ВИД ПЛАКАТОВ

3) ТАБЛИЦА ИНТЕГРАЛОВ, ПРОИЗВОДНЫХ И ПРЕОБРАЗОВАНИЙ ЛАПЛАСА

Функция

Производная

Интеграл

1

4) СВОЙСТВА ДЕЛЬТА-ФУНКЦИИ ПРИ ВЫЧИСЛЕНИИ ИНТЕГРАЛОВ

Вид стандартизирующей функции со всеми возможными комбинациями:

Общее решение для расчета выходной распределенной величины:

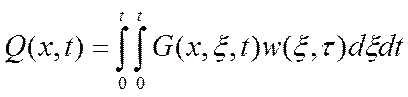
Составляющие решения:

МОДЕЛИРОВАНИЕ СИСТЕМ НА МИКРО- И МАКРОУРОВНЕ

Методические указания к выполнению курсового проекта

по дисциплине «Моделирование систем» для студентов специальности 210100 вечерней формы обучения

Составил:             Мефедова Юлия Александровна

                                        Рецензент             Т.Н. Скоробогатова

Редактор               Л.В.Максимова

Корректор            А.М.Рогачева

Подписано в печать

Формат 60х84 1/16

Бумага   тип.

Усл. печ. л. 0,75

Уч.-изд.л. 0,659

Тираж    100     экз.

Заказ

Бесплатно

Саратовский государственный технический университет

410054, г.Саратов, ул.Политехническая, 77

Копипринтер БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140

Скачать файл