Моделирование на микро- и макроуровне. Построение математической модели колебания круглой мембраны. Исследование гидравлической системы

СОДЕРЖАНИЕ

Введение                                                                    3

1    Моделирование на микроуровне                       4

1.1 Исходные данные                                                4

1.2 Идентификация краевой задачи                                                                                    4

1.3 Расчёт выходной распределенной величины   6

1.4 Расчёт динамической характеристики              9

2    Моделирование на макроуровне                     12

2.1 Графические формы математической модели гидравлической системы          12

2.2 Расчет параметров гидравлической системы 14

2.3 Узловой метод формирования математической модели гидравлической системы                                                                  16

2.4 Метод Ньютона для анализа статической модели технической системы                                                                  19

2.5 Метод Эйлера для анализа динамической модели технической системы        23

Заключение                                                                                                27

Список используемых источников                                                                                               28

Приложение А                                                                                               29

ВВЕДЕНИЕ

Существуют среды, которые не могут быть математически описаны в пространстве сосредоточенных параметров (например, электромагнитное поле, электростатическое поле, течение потока, температура и т. д.).

Системой с распределенными параметрами (СРП) называется система, в которой практически все сигналы (в первую очередь – входной и выходной) являются функциями пространственных координат и времени.

Математически СРП описываются дифференциальными уравнениями в частных производных. Также для этого вводятся функции Грина, континуальная и интегральная передаточные функции.

Система с сосредоточенными параметрами (ССП) является частным случаем СРП и вводится для упрощения и решения задач на первом этапе. В большинстве случаев такого упрощения оказывается достаточно для получения адекватных результатов, но в ряде задач распределение параметров в пространстве оказывает существенное воздействие на результаты. В этом случае применяется аппарат теории СРП.

Целью данной работы является моделирование на микро и макроуровне. При моделировании на микроуровне необходимо построить математическую модель колебания круглой мембраны. На макроуровне исследуется гидравлическая система. При разработке и исследовании модели макроуровня необходимо выполнить: синтез моделей в графической и матричный формах, в виде системы обыкновенных дифференциальных уравнениях, а также анализ полученной математической модели в статическом и динамическом режиме.

1 МОДЕЛИРОВАНИЕ НА МИКРОУРОВНЕ

1.1  Исходные данные

Исходные данные для выполнения первой части курсового проекта:

1) Уравнение колебания мембраны:

(1)

2) Начальные условия:

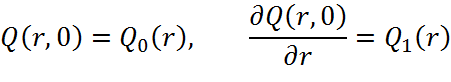
3) Граничные условия:

, ,

4) Стандартизирующая функция:

                               (2)

5) Функция Грина:

– положительные корни уравнения

(3)

6) Континуальная передаточная функция:

(4)

1.2  Идентификация краевой задачи

Уравнение (1) представляет собой одномерное уравнение гиперболического типа, имеющую вторую производную по времени t. Данное уравнение описывает колебательные процессы мембраны. Данная мембрана имеет радиус 0,2 метра и толщину 0,001 метра. Материал мембраны – резина, модуль Юнга E=0.7 кг/мм², поверхностная плотность ρ=1,8  кг/м². Проведём идентификацию всех величин входящих в уравнение (1).

Дифференциальное уравнение имеет вид:

где       Q(r,t) – выходная распределённая величина, представляющая собой ортого­нальную деформацию мембраны, м;

f(r,t) – входное распределённое воздействие на мембраны, м/c².

Для уравнения (1) формулируются следующие условия:

- начальные условия: ;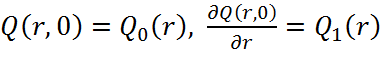

- граничные условия: , , , .

Стандартизирующая функция, компенсирующая влияние начальных и гра­ничных условий для данной одномерной задачи имеет вид (2).

Функция Грина, являющаяся решением краевой задачи при начальных и гра­ничных условиях и входном воздействии в виде δ-функции имеет вид (3).

Континуальная передаточная функция, являющаяся преобразованием Лап­ласа функции Грина имеет вид (4).

Для решения частной задачи примем следующие условия:

- входное воздействие:

f(r,t)=0,5∙cos(0.1∙t);

- начальные  условия,  описывающие положение и скорость мембраны в начальный момент времени:

, ;

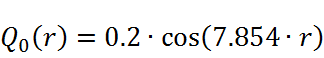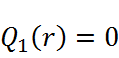- граничные условия, описывающие колебание мембраны:

, , , .

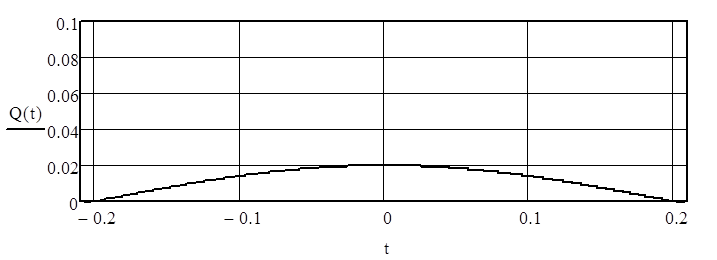
Представим на рисунке 1 изображение мембраны в начальный момент времени:

Рисунок 1 – Изображение мембраны в начальный момент времени

Волновая скорость мембраны:

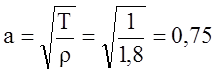 м/с

С учётом входного воздействия, принятых начальных и граничных условий стандартизирующая функция принимает вид:

,

где       δ^'(t) – импульсная переменная функции.

1.3 Расчёт выходной распределенной величины

Идентификация исходного уравнения позволяет перейти к расчету распреде­ленной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная компози­ция от произведения функции Грина на стандартизирующую функцию:

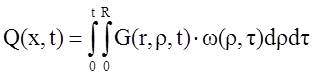                                                                        (5)

Выходная величина Q(x,t) находится как сумма двух составляющих:

Q(x,t)=Q₁(x,t) + Q₂(x,t)                                                                                      (6)

где       Q₁(x,t) и Q₂(x,t) – первая и вторая составляющие выходной величины и находятся как:

	(7)
	(8)

Вынесем постоянные за знак интеграла первой и второй составляющей выходной функции:

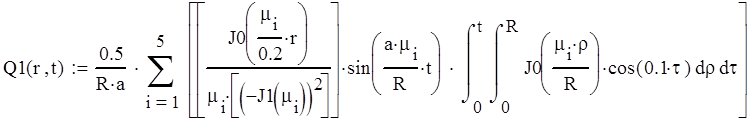             (9)

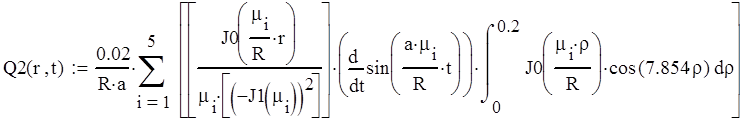               (10)

Определим μ₁- μ₅:

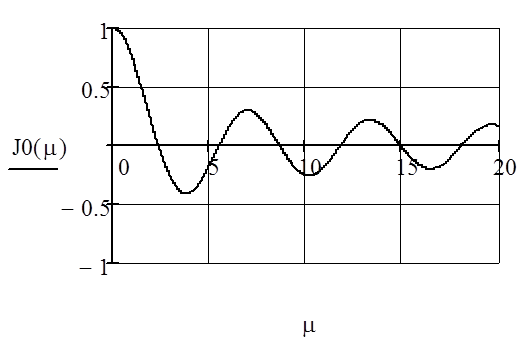
Рисунок 2 – График функции Бесселя J₀(μ)

По графику определим положительные корни уравнения J₀(μ)=0:

;; ; ; .

Используя программный продукт Mathcad 15 подставим (9) и (10) в (6) и построим график при фиксированном времени t.

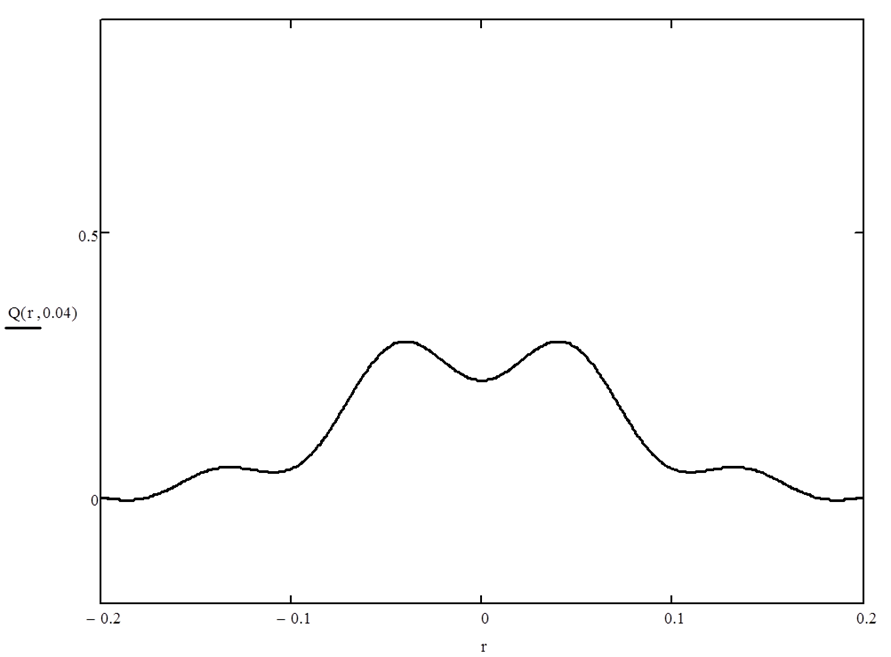
Рисунок 3 – График выходной величины Q(r,t) при t=0.04с

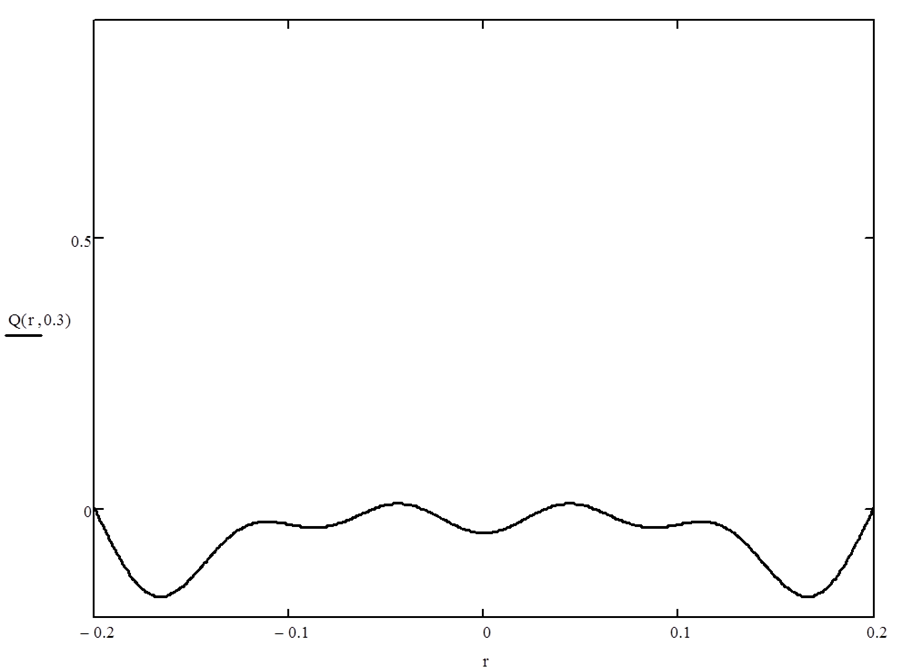
Рисунок 4 – График выходной величины Q(r,t) при t=0,3с

Построим 3D график колебаний мембраны в Mathcad 15 (Рисунок 5):

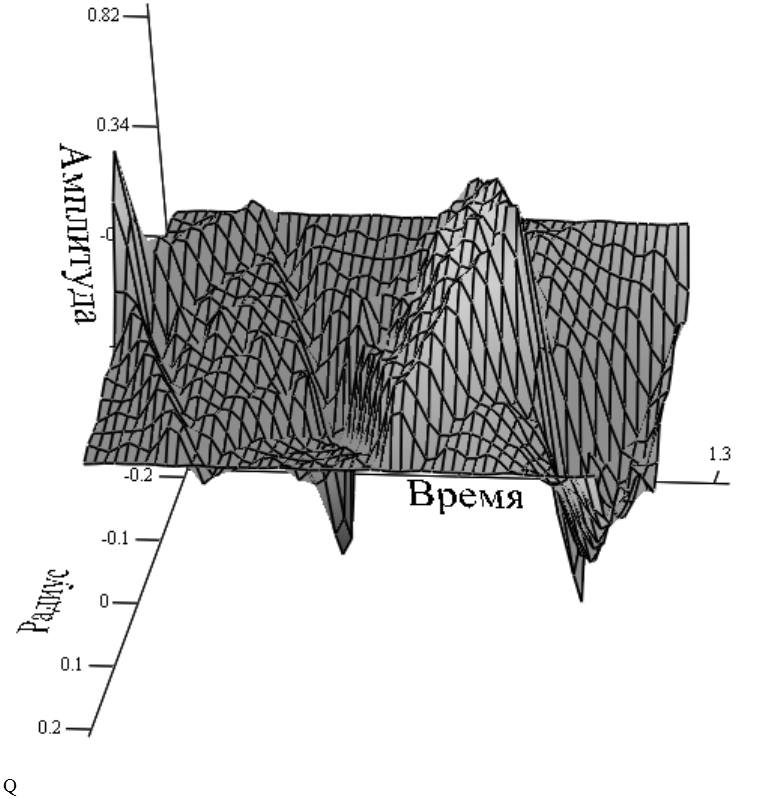
Рисунок 5 – График нагрева диска в 3D

1.4 Расчёт динамической характеристики

Выполним преобразование Лапласа от стандартизирующей функции. В результате получим:

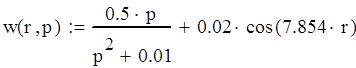
Континуальная передаточная функция имеет вид:

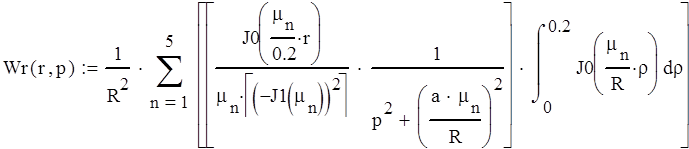
В выражении для интегральной передаточной функции сделаем замену

Получим:

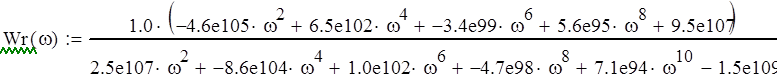
По полученной передаточной функции построим ЛАЧХ. Найдем выражение для логарифмической амплитудно-частотной характеристики:

На рисунке 6 представим ЛАЧХ, построенную в программе MathCad 15. Аппроксимируя полученную ЛАЧХ её стандартными типовыми накло­нами получаем 0 дб/дек и -40 дб/дек, что соответствует апериодическому звену первого порядка. Тогда передаточная функция будет иметь вид: