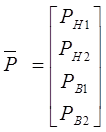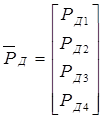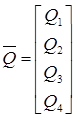Другие предметы \ Моделирование систем управления

Моделирование на микро- и макроуровне. Построение математической модели колебания круглой мембраны. Исследование гидравлической системы, страница 3

, , , .

Вычислим матричное произведение слагаемых правой части уравнения: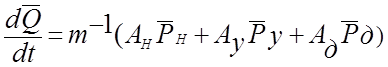

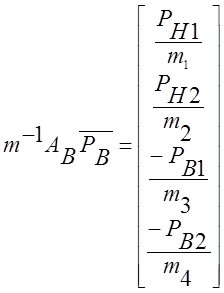
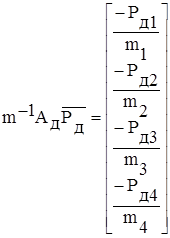
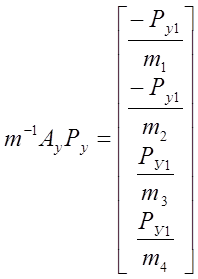Складываем полученные матрицы в соответствии с уравнением 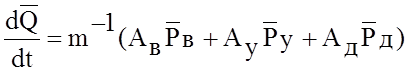и учитываем зависимость

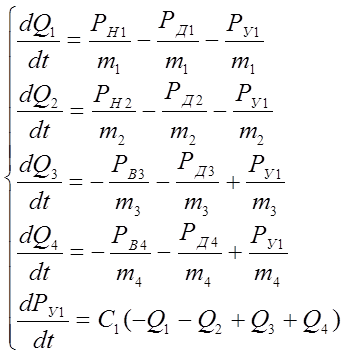(1)

Давления диссипативных элементов на основании формулы :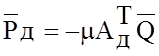

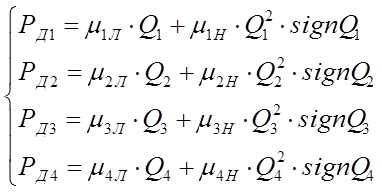(2)

С учетом численных значений параметров модели, найденных во второй работе, уравнения (1) приобретает вид:

(3)

А давления диссипативных элементов:

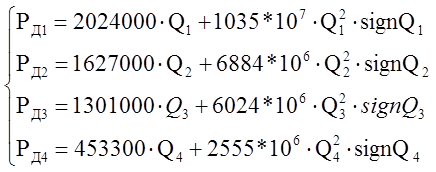(4)

Для рассмотрения статического состояния система дифференциальных уравнений (1) приобретает вид:

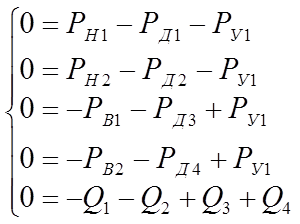(5)

Выполним преобразования (5) с учетом (4), получают:

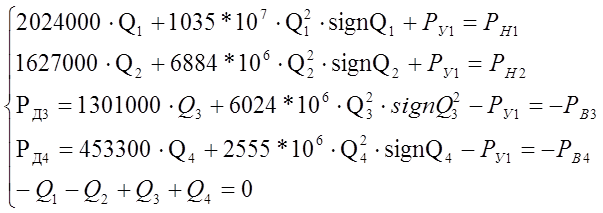(6)

Таким образом, система уравнений (3), (4) является динамической моделью гидравлической системы, а (6) – статической моделью.

2.4 Метод Ньютона для анализа статической модели технической системы

Система дифференциальных уравнений, характеризующая динамическую модель гидравлической системы, полученной с использованием узлового метода:

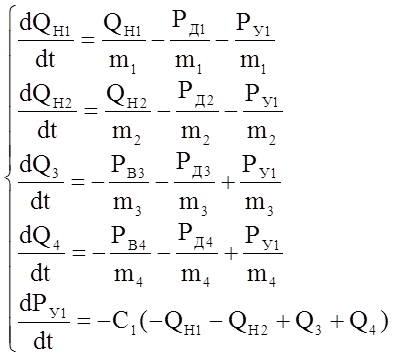(7)

При постоянных внешних воздействиях система (7) находится в установившемся равновесном состоянии. Её фазовые координаты при этом постоянны, такой режим функционирования системы называется статический. Статическое состояние гидросистемы достигается при постоянных внешних воздействиях:

1) подачей насосов Qн1,Qн2;

2) давлениями потребителей Рв1,Рв2.

При этом устанавливаются постоянные значения фазовых координат:

1) расходы в гидромагистралях Q3, Q4;

2) давление в упругом элементе Ру1.

Полагая 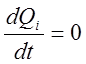и 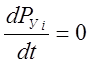, получим следующую систему нелинейных алгебраических элементов:

Компонентное уравнение в диссипативных элементах в гидросистеме носит более сложный характер. При этом выделяют линейные и нелинейные потери давления в гидромагистрали и их компонентные уравнения, запишутся виде:

., i =1..5

(8)

где – коэффициент гидравлического сопротивления, характеризующий линейные потери при ламинарном режиме движения жидкости.

– коэффициент гидросопротивления характеризующий нелинейные потери при турбулентном режиме движения жидкости.

С учетом уравнения (8), преобразуем систему к следующему виду:

(9)

Полученная система уравнений является статической моделью системы, где в правой части известны значения входных воздействий. Для ее решения используется различные численные методы, для которых предварительно необходимо составить матрицу Якоби.

Матрица Якоби характеризует важнейшие свойства физической системы, а так же свойства уравнений математической модели. Элементами матрицы Якоби, являются частные производные от нелинейной вектор функции F(V) = (f₁,f₂ …f_n) по фазовым коэффициентам системы (Q₃, Q₄, Ру₁), т.е.:

(10)

В системе уравнений, нелинейной является функция , для них частные производные имеют вид:

(11)

Тогда матрица Якоби, исследуемой гидросистемы, имеет вид:

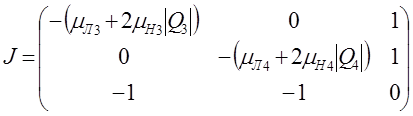
Для решения статической модели используем численный метод Ньютона, алгоритм которого включает следующие этапы:

– выбор начального приближения ,

где – вектор фазовых координат (Q₃, Q₄, Ру₁),

– нулевой вектор-столбец;

– вычисление матрицы Якоби в точке (k=0, 1 2 …);

– вычисление вектора невязок . Вектор невязок получается из системы уравнений (4) для статического режима:

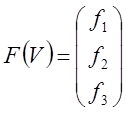
– определение вектора поправок:

– определение нового приближения вектора искомых фазовых переменных:

– проверка условий окончания итерационного процесса, при выполнении условия, что и соизмеримы (совпадают до десятых), иначе осуществляется переход на предыдущие этапы и вычисляется следующая итерация.

Расчет фазовых координат при статическом процессе произведен в математическом пакете MathCad 15 (Рисунок 5). Результаты вычислений представлены в таблице 1

Таблица 5 – Результаты статического анализа

Фазовые координаты	Qн1=200∙10^-6 м³/c Qн2=0∙10^-6 м³/c	Qн1=200∙10^-6 м³/c Qн2=400∙10^-6 м³/c
Q₃, м³/c
Q₄, м³/c
Ру₁, Па

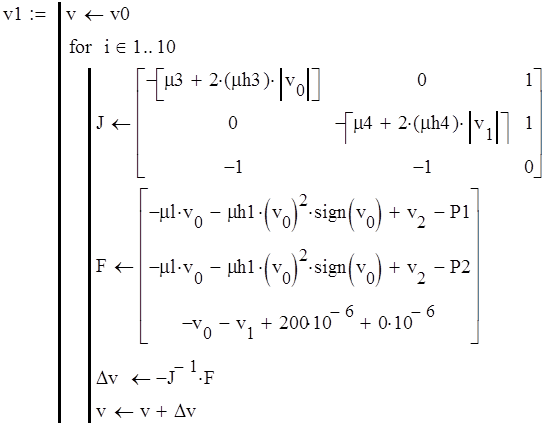
Рисунок 4 – Программа для расчета статической модели в MathCAD 15

2.5 Метод Эйлера для анализа динамической модели технической системы

Так как система дифференциальных уравнений нелинейная, то элементами матрицы Якоби, являются частные производные по фазовым координатам:

Матрица Якоби в динамическом случае переменная, ее элементы зависят от фазовых координат системы - расходов жидкости .

Пусть начальное и конечное значения заданы в виде (рассчитаны с использованием статической модели в четвертой работе):

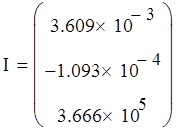
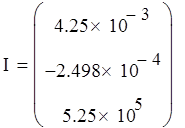
Вектор входных воздействий при :

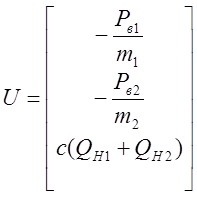
Произведем расчет значений матрицы Якоби с учетом начальных значений расходов:

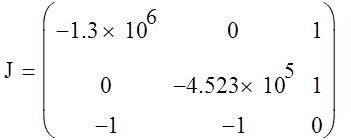
Запишем единичную матрицу:

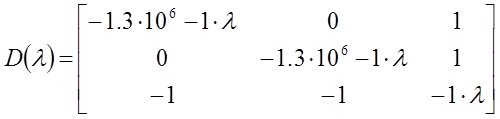
Тогда характеристическое уравнение имеет вид:

Вычислив корни характеристического уравнения, найдены собственные значения матрицы Якоби:

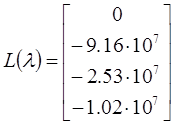
Все корни характеристического уравнения имеют отрицательные действительные части, что говорит об устойчивости самой системы. Отсутствие комплексно – сопряженных дает монотонный процесс ряда фазовых координат. Рекомендуемый шаг интегрирования равный h=0.5. Выполним проверку устойчивости, методом Эйлера при данном шаге:

Следовательно, шаг h=0.5 обеспечит, устойчивость метода, то есть приемлемую точность вычислений.

Программа в MathCad 15, реализующая данный алгоритм имеет вид:

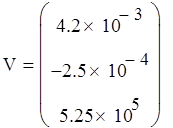
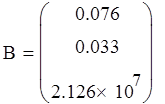
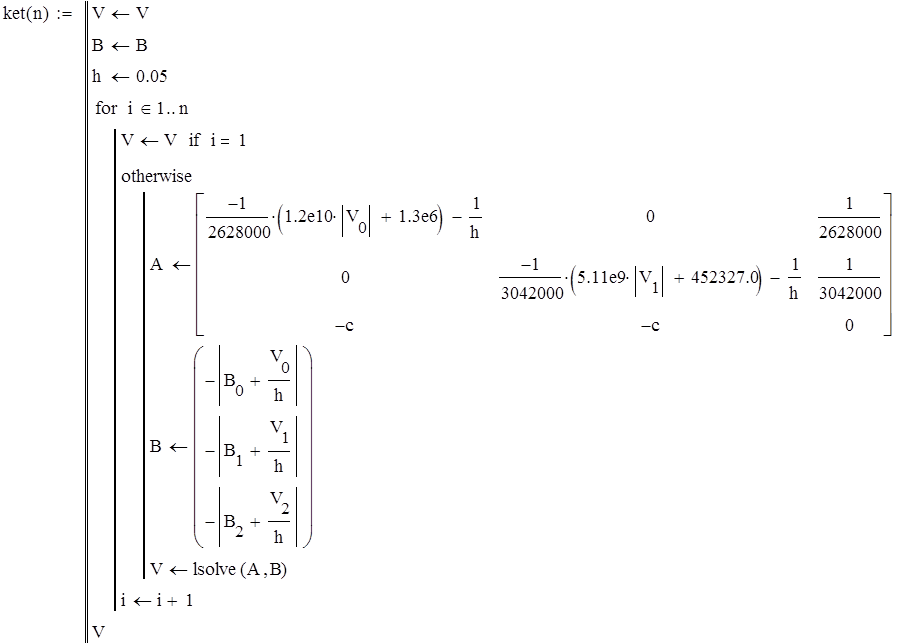
Построим переходные процессы.

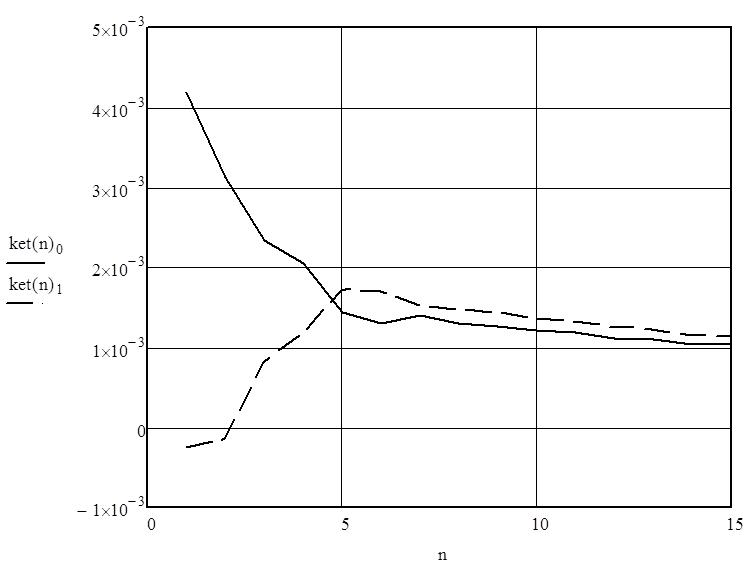
Рисунок 5 – Переходные процессы системы (расходы)

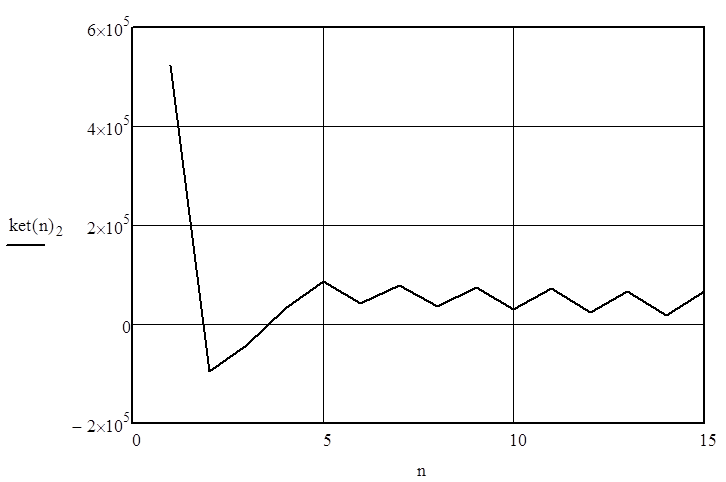
Рисунок 6 – Переходный процесс системы (давление)

ЗАКЛЮЧЕНИЕ

В данной курсовой работе был произведен расчет математической модели на микро и макроуровне. При моделировании на микроуровне был произведен расчет математической модели колебания мембраны. В ходе расчета была произведена идентификация краевой задачи, расчёт выходной распределенной величины, расчёт динамической характеристики, построен график ЛАЧХ и определена передаточная функция по аппроксимированной ЛАЧХ. При моделировании на макроуровне был были построены графические формы математической модели гидравлической системы, произведен расчет ее параметров, рассчитаны узловой метод формирования математической модели, метод Ньютона для анализа статической модели технической системы, метод Эйлера для анализа динамической модели.

1 2 3 4

Скачать файл