СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Анисимов И. В. Основы автоматического управления технологическими прцессами химической прмышленности. Л., Химия, 1967. 408с.
2. Баранов В.Я. Промышленные приборы и средства автоматизации. Справочник, 1987.
3. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. М., Наука, 1975. 767с.
4. Жарковский Б.И. Приборы автоматического контроля и регулирования: учебник для ПТУ. - М.: Высшая школа, 1989. - 450с.
5. Иващенко Н. Н. Автоматическое регулирование. М., Машиностроение, 1978. 735с.
ПРИЛОЖЕНИЕ А
1. Моделирование на микроуровне 30
2Моделирование на макроуровне 31
2.1 Исходные данные 31
2.2 Расчет трубопровода и матрица инциденций 32
2.3Узловой метод, метод Ньютона, метод Эйлера 33
|
Исходные данные |
|
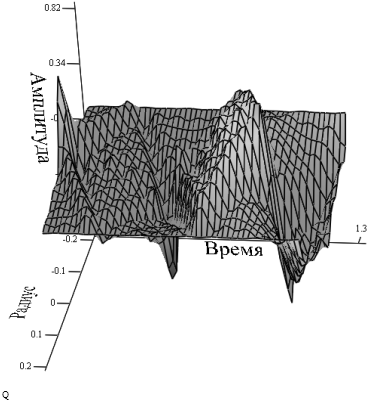
Уравнение колебания мембраны |
|
|
|
Начальные условия |
|
|
|
Граничные условия |
|
|
|
Стандартизирующая функция |
|
|
|
Функция Грина |
|
|
|
Континуальная передаточная функция |
|
|
|
f(r,t)=0,5∙cos(0.1∙t) |
|
|
|
|
|
|
![]()
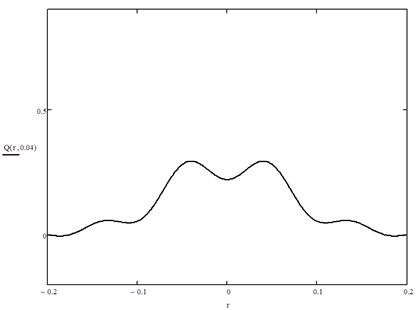
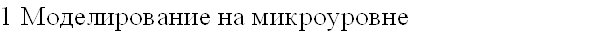
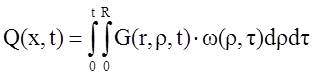 - выходная величина.
- выходная величина.
Q(x,t)=Q1(x,t)
+ Q2(x,t) 

![]()

|
|
|
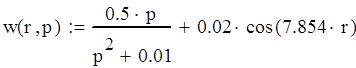 - преобразование
- преобразование
![]()
![]()
![]()
![]()
![]()
 Лапласа от
стандартизирующей функции
Лапласа от
стандартизирующей функции
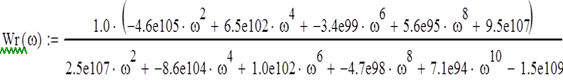
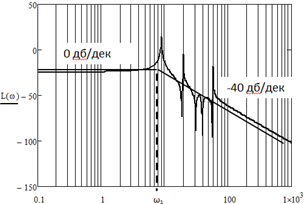
![]() от
континуальной передаточной функции
от
континуальной передаточной функции
![]()
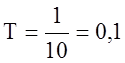 [с]
[с]
20∙lgk = -24, 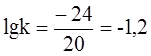
![]()
![]()
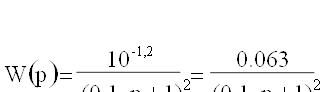
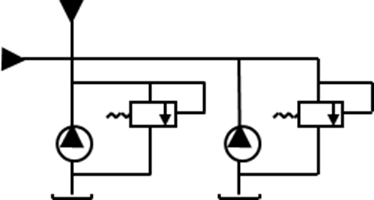
Принципиальная схема гидросистемы
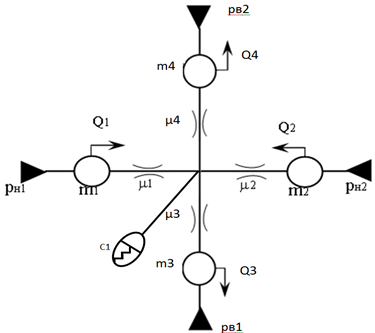
Динамическая модель гидросистемы
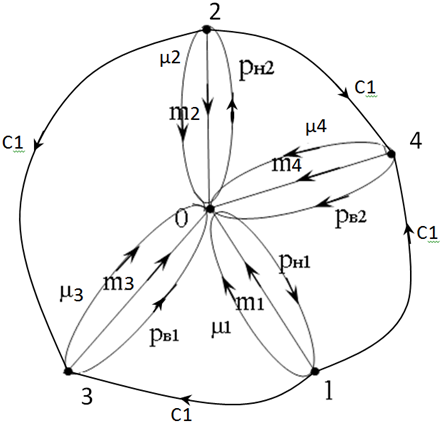
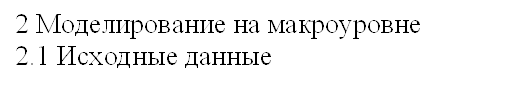 Ориентированный граф гидросистемы
Ориентированный граф гидросистемы
Таблица 1 – Исходные данные
|
Обозначение |
Основные параметры |
Значение |
|
|
Плотность рабочей жидкости |
860 кг/м3 |
|
|
Вязкость |
0,15·10-4 м2/с |
|
ЕС |
Модуль упругости газожидкостной смеси |
1,7·108 Па |
|
Етр |
Модуль упругости трубопровода |
2,1·1011 Па |
|
|
Коэффициент потерь на трение при турбулентном потоке |
0,03 |
|
|
Толщина стенки трубопровода |
2∙10-3 м |
Таблица 2 – Параметры трубопроводов
|
Параметр |
Номер трубопровода |
|||
|
1 |
2 |
3 |
4 |
|
|
Диаметр трубопровода dтр, м |
0,025 |
0,03 |
0,03 |
0,032 |
|
Длина трубопровода l, м |
1,5 |
2,5 |
2 |
0,9 |
|
Коэффициент местных сопротивлений ξ |
4 |
5,5 |
5 |
3 |
|
Давление потребителей и насосов P, ∙106 Па |
0,2 |
0,25 |
0,3 |
0.25, 0.5 |
 Таблица 3 –
Результаты расчета
трубопровода
Таблица 3 –
Результаты расчета
трубопровода
|
Параметры |
Формула |
Магистраль |
|||
|
1 |
2 |
3 |
4 |
||
|
1. Площадь сечения магистрали |
|
0.00049 |
0.0007 |
0.0007 |
0,0008 |
|
2. Объём участка трубопровода |
|
0.00074 |
0.0018 |
0.0014 |
0,00072 |
|
3. Доля объёма |
|
0.188 |
0.451 |
0.361 |
0,185 |
|
4. Коэффициент массы |
|
2628000 |
3042000 |
2433000 |
962400 |
|
5. Коэффициент линейных |
|
2024000 |
1627000 |
1301000 |
453300 |
|
6. Коэффициент нелинейных |
|
1035∙107 |
6884∙106 |
6024∙106 |
2555∙106 |
|
7. Коэффициент жесткости участка |
|
1035∙109 |
2107∙108 |
3292∙108 |
1255∙109 |
Общий коэффициент жесткости при разветвлении трубопровода:
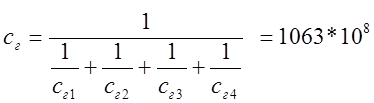
Таблица 4 - Матрица инциденций гидравлической системы
|
Узлы |
Ветви |
|||||
|
Источники потенциалов |
Упругие |
|||||
|
рН1 |
рН2 |
рВ1 |
рВ2 |
с1 |
||
|
1 |
1 |
0 |
0 |
0 |
-1 |
|
|
2 |
0 |
1 |
0 |
0 |
-1 |
|
|
3 |
0 |
0 |
-1 |
0 |
1 |
|
|
4 |
0 |
0 |
0 |
-1 |
1 |
|
|
АВ |
АУ |
|||||
|
Узлы |
Ветви |
|||||||
|
Диссипативные |
Инерционные |
|||||||
|
μ1 |
μ2 |
μ3 |
μ4 |
m1 |
m2 |
m3 |
m4 |
|
|
1 |
-1 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
0 |
0 |
-1 |
0 |
0 |
|
3 |
0 |
0 |
-1 |
0 |
0 |
0 |
-1 |
0 |
|
4 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
-1 |
|
АД |
АИ |
|||||||
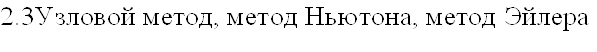
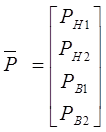 ,
,![]() ,
,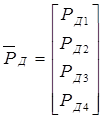 ,
,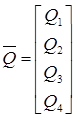 .
.
Матрица потенциалов источников Рв, упругих Ру и диссипативных Рд, элементов и матрица фазовых переменных типа потока Q
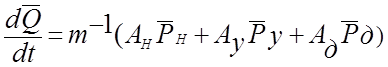

![]()

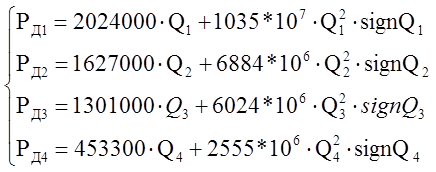
Давления диссипативных элементов на основании формулы
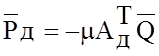
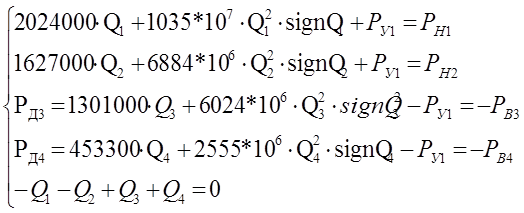 Статическая модель
Статическая модель
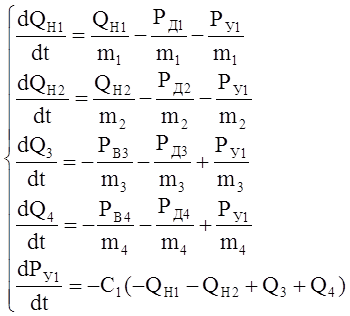
Динамическая модель гидросистемы
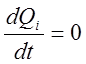 ,
, 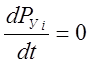
|
|
Система нелинейных уравнений для статической модели |
![]()
![]()
![]()
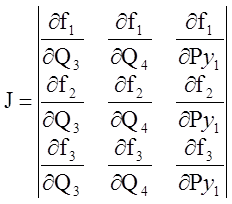
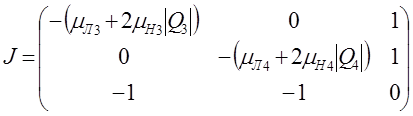
|
Фазовые координаты |
Qн1=200∙10-6 м3/c Qн2=0∙10-6 м3/c |
Qн1=200∙10-6 м3/c Qн2=400∙10-6 м3/c |
|
Q3, м3/c |
|
|
|
Q4, м3/c |
|
|
|
Ру1, Па |
|
|
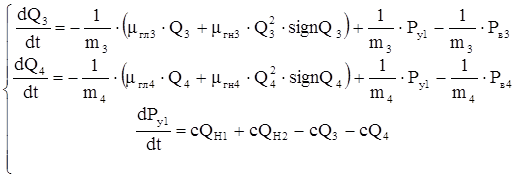
Динамическая модель гидросистемы
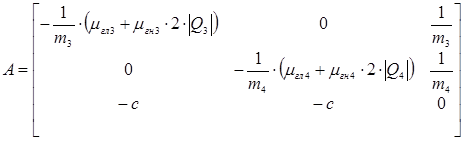
Матрица Якоби
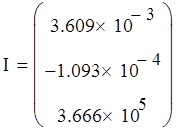
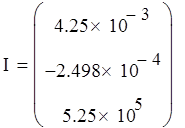
Начальное и конечное значение
|
|
Матрица Якоби |
![]()
Характеристическое уравнение
|
|
Корни характеристического уравнения (все отрицательные, действительные числа) |
![]()
![]()
![]()
![]()
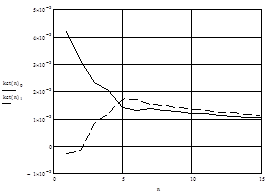
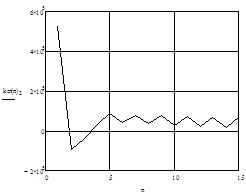
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.